Solved Examples: Applied Problems on Integrals

(1.) A garden wall is built along a straight 2‑foot section of ground.
At the left end, the wall is 3 feet tall, and at the right end, it is 9 feet tall.
The top of the wall rises in a straight line between these two points, so the side profile of the wall forms a trapezoid.
Label the vertices with coordinates (0, 0) and (2, 0) for the bottom corners, and (0, 3) and (2, 9) for the top corners.
Algebra: Find the equation of the line representing the sloping top edge of the wall.
Coordinate Geometry: Sketch the graph and indicate the trapezoid formed by the ground (the base), the two vertical ends of the wall (the legs), and the sloping top edge.
Mensuration/Plane Geometry: Determine the area of this trapezoid using the trapezoid area formula.
Calculus: Calculate the area of the trapezoid using a definite integral, and compare your result with the geometric method.

The sloping egde of the wall is the straight line joining the top corners.
Let us find the equation of that line.

$ \underline{\text{Algebra}} \\[3ex] \text{Point 1} = (0, 3) \\[3ex] x_1 = 0 \\[3ex] y_1 = 3 \\[3ex] \text{Point 2} = (2, 9) \\[3ex] x_2 = 2 \\[3ex] y_2 = 9 \\[3ex] \text{Slope, } m = \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex] m = \dfrac{9 - 3}{2 - 0} \\[5ex] m = \dfrac{6}{2} \\[5ex] m = 3 \\[3ex] \text{y-intercept, } b = 3 \\[3ex] y = mx + b ...\text{Equation of a Straight Line in Slope-Intercept Form} \\[3ex] y = 3x + 3 \\[3ex] $ Coordinate Geometry
The graph with the indicated trapezoid is shown below.

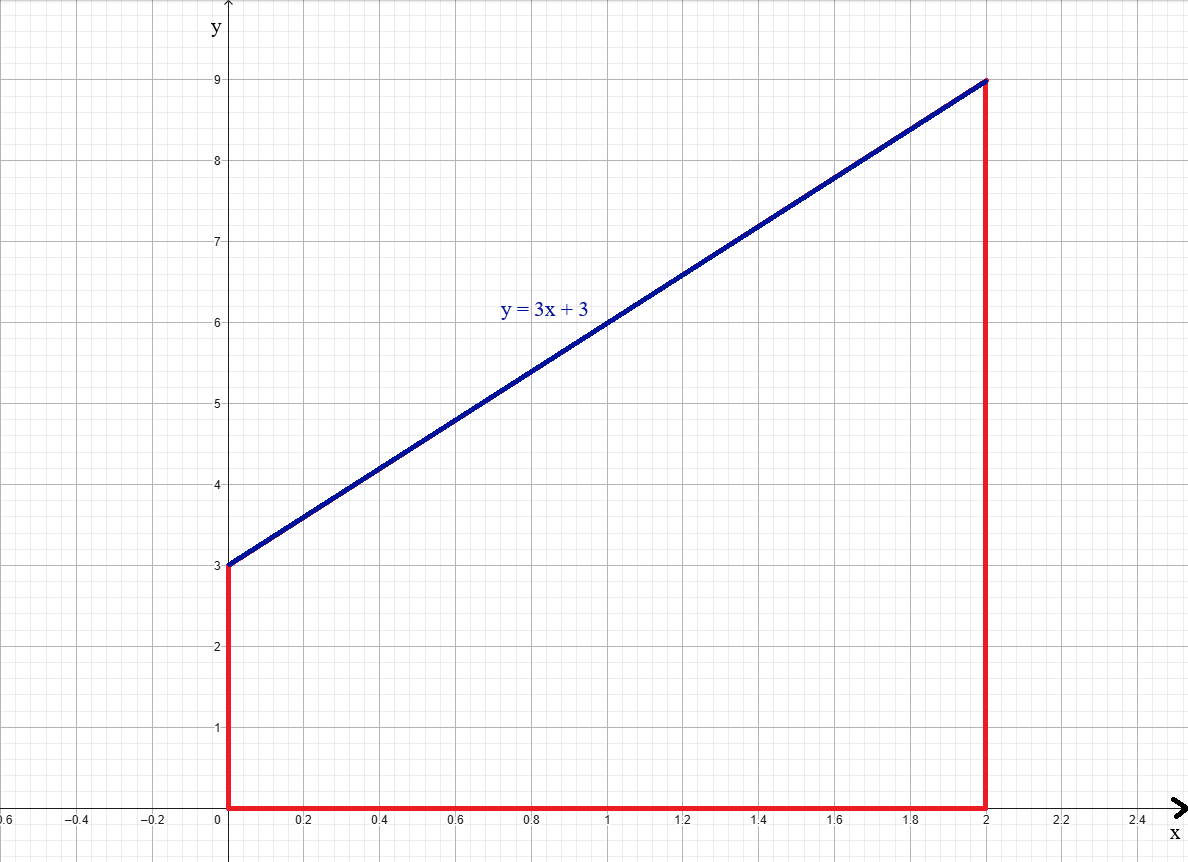
Number 1

$ \underline{\text{Mensuration}} \\[3ex] \text{Area of the trapezoid} = \dfrac{2(3 + 9)}{2} \\[5ex] = 12\;ft^2 \\[5ex] \underline{\text{Calculus}} \\[3ex] \text{Area of the trapezoid} = \displaystyle\int_0^2 (3x + 3)\;dx \\[5ex] = \left[\dfrac{3x^2}{2} + 3x\right]_0^2 \\[5ex] = \left[\dfrac{3(2)^2}{2} + 3(2)\right] - \left[\dfrac{3(0)^2}{2} + 3(0)\right] \\[5ex] = (6 + 6) - (0 + 0) \\[3ex] = 12\;ft^2 \\[3ex] $ The result from the Calculus-based approach is the same as the result from a Geometric-based approach.

(2.)

$ Let\;\; velocity = v \\[3ex] s(t) = t^3 - 2t^2 + t + 1 \\[3ex] v = \dfrac{ds}{dt} = 3t^2 - 4t + 1 \\[3ex] After\;\;2\;\;seconds \implies t = 2 \\[3ex] v = 3(2)^2 - 4(2) + 1 \\[3ex] v = 12 - 8 + 1 \\[3ex] v = 5\;m/s $

(3.)

$ C(x) = \text{cost function} \\[3ex] R(x) = \text{revenue function} \\[3ex] P(x) = \text{profit function} \\[3ex] (a) \\[3ex] C(x) = 3.6x^2 + x \\[3ex] C(15) = 3.6(15)^2 + 15 \\[3ex] C(15) = 3.6(225) + 15 \\[3ex] C(15) = \$825.00 \\[3ex] (b) \\[3ex] R(x) = 73 * x = 73x \\[3ex] P(x) = R(x) - C(x) \\[3ex] P(x) = 73x - (3.6x^2 + x) \\[3ex] P(x) = 73x - 3.6x^2 - x \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] (c) \\[3ex] $ We can solve this question part using at least two approaches.
Vertex Method: the x-coordinate of the vertex gives the number of mats that should be sold to maximise the profit.
The y-coordinate of the vertex gives the maximum profit.

$ \underline\text{{Vertex Method}} \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] a = -3.6,\;\; b = 72,\;\; c = 0 \\[3ex] x-coordinate \text{ of Vertex} \\[3ex] = -\dfrac{b}{2a} \\[5ex] = -\dfrac{72}{2(-3.6)} \\[5ex] = -\dfrac{72}{-7.2} \\[5ex] = 10 \\[3ex] $ 10 mats should be produced and sold to maximise profit.

$ \underline\text{{Differential Calculus Approach}} \\[3ex] P(x) = -3.6x^2 + 72x \\[3ex] P'(x) = -7.2x + 72 \\[3ex] \text{Set } P'(x) = 0 \text{ and solve for } x \\[3ex] -7.2x + 72 = 0 \\[3ex] -7.2x = -72 \\[3ex] x = \dfrac{-72}{-7.2} \\[5ex] x = 10 \\[3ex] $ 10 mats should be produced and sold to maximise profit.

(4.)

We can solve this question part using at least two approaches.
Vertex Method: the x-coordinate of the vertex is the number of bags that will give the maximum profit.
The y-coordinate of the vertex is the maximum profit.

$ \underline\text{{Vertex Method}} \\[3ex] y = 10x - x^2 \\[3ex] y = -x^2 + 10x \\[3ex] y = ax^2 + bx + c \\[3ex] a = -1, b = 10 \\[3ex] x-coordinate \text{ of Vertex} \\[3ex] = -\dfrac{b}{2a} \\[5ex] = \dfrac{-10}{2(-1)} \\[5ex] = \dfrac{-10}{-2} \\[5ex] = 5 \\[3ex] $ The sale of 5 bags will give the maximum profit.

$ \underline\text{{Differential Calculus Approach}} \\[3ex] y = 10x - x^2 \\[3ex] \dfrac{dy}{dx} = 10 - 2x \\[3ex] 10 - 2x = 0 \\[3ex] 10 = 2x \\[3ex] 2x = 10 \\[3ex] x = \dfrac{10}{2} \\[3ex] x = 5 \\[3ex] $ The sale of 5 bags will give the maximum profit.

(9.) KCSE A particle was moving along a straight line.
The acceleration of the particle after t seconds was given by $(4t - 13)\;ms^{-2}$.
The initial velocity of the particle was 18 $ms^{-1}$
(a) Determine the value of t when the particle is momentarily at rest.
(b) Find the distance covered by the particle between the time t = 1 second and t = 3 seconds.

$ a = 4t - 13 \\[3ex] a = \dfrac{dv}{dt} \\[5ex] dv = a dt \\[3ex] v = \displaystyle\int a dt \\[3ex] v = \displaystyle\int (4t - 13) dt \\[3ex] v = \dfrac{4t^2}{2} - 13t + C \\[3ex] v = 2t^2 - 13t + C \\[3ex] when\;\;t = 0,\;\;initial\;\;velocity = v = 18\;ms^{-1} \\[3ex] \implies \\[3ex] 18 = 2(0)^2 - 13(0) + C \\[3ex] 18 = 0 - 0 + C \\[3ex] 18 = C \\[3ex] C = 18 \\[3ex] v = 2t^2 - 13t + 18 \\[3ex] (a) \\[3ex] momentarily\;\;at\;\;rest\implies v = 0 \\[3ex] 0 = 2t^2 - 13t + 18 \\[3ex] 2t^2 - 13t + 18 = 0 \\[3ex] 2t(t - 2) - 9(t - 2) = 0 \\[3ex] (t - 2)(2t - 9) = 0 \\[3ex] t - 2 = 0 \;\;\;OR\;\;\; 2t - 9 = 0 \\[3ex] t = 2 \;\;\;OR\;\;\; 2t = 9 \\[3ex] t = 2\;s \;\;\;OR\;\;\; t = \dfrac{9}{2}\;s \\[3ex] (b) \\[3ex] v = \dfrac{dd}{dt} \\[5ex] dd = vdt \\[3ex] d = \displaystyle\int v dt \\[3ex] $ The zeros of the function...where the graph include areas above or below the x-axis (t-axis) are t = 2 seconds and t = $\dfrac{9}{2} = 4.5$ seconds
But we are asked to calculate the area (distance covered) between t = 1 second and t = 3 seconds
So, we have to first calculate the area between t = 1 second and t = 2 seconds
Then, we calculate the area between t = 2 seconds and t = 3 seconds
Because 4.5 seconds is greater than 3 seconds, we skip that area.

$ v = \displaystyle\int_1^2 (2t^2 - 13t + 18) dt + \displaystyle\int_2^3 (2t^2 - 13t + 18) dt \\[5ex] v = \left[\dfrac{2t^3}{3} - \dfrac{13t^2}{2} + 18t\right]_1^2 + \left[\dfrac{2t^3}{3} - \dfrac{13t^2}{2} + 18t\right]_2^3 \\[5ex] \left[\dfrac{2t^3}{3} - \dfrac{13t^2}{2} + 18t\right]_1^2 \\[5ex] t = 2\;s \\[3ex] \dfrac{2(2)^3}{3} - \dfrac{13(2)^2}{2} + 18(2) \\[5ex] \dfrac{16}{3} - \dfrac{26}{1} + \dfrac{36}{1} \\[5ex] \dfrac{16 - 78 + 108}{3} \\[5ex] \dfrac{46}{3}\;m \\[5ex] t = 1\;s \\[3ex] \dfrac{2(1)^3}{3} - \dfrac{13(1)^2}{2} + 18(1) \\[5ex] \dfrac{2}{3} - \dfrac{13}{2} + \dfrac{18}{1} \\[5ex] \dfrac{4 - 39 + 108}{6} \\[5ex] \dfrac{73}{6}\;m \\[5ex] Area = \dfrac{46}{3} - \dfrac{73}{6} = \dfrac{92 - 73}{6} = \dfrac{19}{6}\;m \\[5ex] \left[\dfrac{2t^3}{3} - \dfrac{13t^2}{2} + 18t\right]_2^3 \\[5ex] t = 3\;s \\[3ex] \dfrac{2(3)^3}{3} - \dfrac{13(3)^2}{2} + 18(3) \\[5ex] \dfrac{18}{1} - \dfrac{117}{2} + \dfrac{54}{1} \\[5ex] \dfrac{36 - 117 + 108}{2} \\[5ex] \dfrac{27}{2}\;m \\[5ex] t = 2\;s \\[3ex] \dfrac{46}{3}\;m \\[5ex] Area = \dfrac{27}{2} - \dfrac{46}{3} = \dfrac{81 - 92}{6} = -\dfrac{11}{6} \\[5ex] Because\;\;Area\;\;cannot\;\;be\;\;negative; \;\;Area = \dfrac{11}{6}\;m \\[5ex] Total\;\;Area = Distance\;\;covered \\[3ex] = \dfrac{19}{6} + \dfrac{11}{6} \\[5ex] = \dfrac{30}{6} \\[5ex] = 5\;m $

(10.) After a long study, tree scientists conclude that a eucalyptus tree will grow at the rate of $0.6 + \dfrac{4}{(t + 1)^3}$ feet per year, where t is time in years.
Find the number of feet that the tree will grow in the third year.

$ \text{Growth rate function, } f(t) = 0.6 + \dfrac{4}{(t + 1)^3} \\[5ex] \text{Total Growth} = \displaystyle\int f(t) dt = \displaystyle\int \left[0.6 + \dfrac{4}{(t + 1)^3}\right] dt \\[5ex] $ The total growth during the 3rd year is the growth that occurs at the end of the second year, t = 2 up to the end of the third year, t = 3.

$ \text{Total Growth during the 3rd year} \\[3ex] = \displaystyle\int_2^3 \left[0.6 + \dfrac{4}{(t + 1)^3}\right] dt \\[5ex] \text{Let us work on the indefinite integral first} \\[3ex] \displaystyle\int \left[0.6 + \dfrac{4}{(t + 1)^3}\right] dt \\[5ex] = \displaystyle\int 0.6 dt + \displaystyle\int \dfrac{4}{(t + 1)^3} dt \\[5ex] = 0.6t + \displaystyle\int \dfrac{4}{(t + 1)^3} dt \\[5ex] \text{For } \displaystyle\int \dfrac{4}{(t + 1)^3} dt \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = t + 1 \\[3ex] \dfrac{dp}{dt} = 1 \\[5ex] \dfrac{dt}{dp} = 1 \\[5ex] dt = dp \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{4}{p^3} dp \\[5ex] = 4\displaystyle\int \dfrac{1}{p^3} dp \\[5ex] = 4\displaystyle\int p^{-3} dp \\[3ex] = 4\dfrac{p^{-3 + 1}}{-3 + 1} \\[5ex] = \dfrac{4p^{-2}}{-2} \\[5ex] = -2p^{-2} \\[3ex] = -\dfrac{2}{p^2} \\[5ex] = -\dfrac{2}{(t + 1)^2} \\[5ex] \implies \\[3ex] \left[0.6t - \dfrac{2}{(t + 1)^2}\right]_2^3 \\[5ex] = \left[0.6(3) - \dfrac{2}{(3 + 1)^2}\right] - \left[0.6(2) - \dfrac{2}{(2 + 1)^2}\right] \\[5ex] = \left[1.8 - \dfrac{2}{4^2}\right] - \left[1.2 - \dfrac{2}{3^2}\right] \\[5ex] = \left[\dfrac{18}{10} - \dfrac{2}{16}\right] - \left[\dfrac{12}{10} - \dfrac{2}{9}\right] \\[5ex] = \left[\dfrac{9}{5} - \dfrac{1}{8}\right] - \left[\dfrac{6}{5} - \dfrac{2}{9}\right] \\[5ex] = \left[\dfrac{72 - 5}{40}\right] - \left[\dfrac{54 - 10}{45}\right] \\[5ex] = \dfrac{67}{40} - \dfrac{44}{45} \\[5ex] = \dfrac{603 - 352}{360} \\[5ex] = \dfrac{251}{360}\;feet $

(20.)

$ \underline{\text{Break-even Point}} \\[3ex] cost = revenue \\[3ex] cost = C(x) = 2000 + 14x + \dfrac{1}{2}x^{\dfrac{2}{3}} \\[7ex] revenue = R(x) = 22 * x = 22x \\[3ex] \implies \\[3ex] 2000 + 14x + \dfrac{1}{2}x^{\dfrac{2}{3}} = 22x \\[7ex] 2000 + 14x - 22x + \dfrac{1}{2}x^{\dfrac{2}{3}} = 0 \\[7ex] 2000 - 8x + \dfrac{1}{2}x^{\dfrac{2}{3}} = 0 \\[7ex] \dfrac{1}{2}x^{\dfrac{2}{3}} - 8x + 2000 = 0 \\[7ex] \dfrac{1}{2}x^{\dfrac{2}{3}} - 8x + 2000 = f(x) \\[7ex] f(x) = \dfrac{1}{2}x^{\dfrac{2}{3}} - 8x + 2000 \\[7ex] f'(x) = \dfrac{2}{3}\left(\dfrac{1}{2}\right)\left(x^{\dfrac{2}{3}} - 1\right) - 8 \\[7ex] f'(x) = \dfrac{1}{3}x^{-\dfrac{1}{3}} - 8 \\[7ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = x_n - \dfrac{\dfrac{1}{2}x_n^{\dfrac{2}{3}} - 8x_n + 2000}{\dfrac{1}{3}x_n^{-\dfrac{1}{3}} - 8} \\[9ex] x_1 = 125 \\[3ex] x_2 = x_1 - \dfrac{\dfrac{1}{2}* x_1^{\dfrac{2}{3}} - 8 * x_1 + 2000}{\dfrac{1}{3} * x_1^{-\dfrac{1}{3}} - 8} \\[9ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* 125^{\dfrac{2}{3}} - 8 * 125 + 2000}{\dfrac{1}{3} * 125^{-\dfrac{1}{3}} - 8} \\[9ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* (\sqrt[3]{125})^2 - 8 * 125 + 2000}{\dfrac{1}{3} * (\sqrt[3]{125})^{-1} - 8} \\[7ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* 5^2 - 8 * 125 + 2000}{\dfrac{1}{3} * 5^{-1} - 8} \\[7ex] x_2 = 125 - \dfrac{\dfrac{1}{2}* 25 - 8 * 125 + 2000}{\dfrac{1}{3} * \dfrac{1}{5} - 8} \\[7ex] x_2 = 125 - \dfrac{12.5 - 1000 + 2000}{\dfrac{1}{15} - 8} \\[7ex] x_2 = 125 - \left(1012.5 \div -\dfrac{119}{15}\right) \\[5ex] x_2 = 125 - \left(1012.5 * -\dfrac{15}{119}\right) \\[5ex] x_2 = 125 - -\dfrac{15187.5}{119} \\[5ex] x_2 = 125 + 127.6260504 \\[3ex] x_2 = 252.6260504 \\[5ex] x_3 = x_2 - \dfrac{\dfrac{1}{2}* x_2^{\dfrac{2}{3}} - 8 * x_2 + 2000}{\dfrac{1}{3} * x_2^{-\dfrac{1}{3}} - 8} \\[9ex] x_3 = 252.6260504 - \dfrac{\dfrac{1}{2}* 252.6260504^{\dfrac{2}{3}} - 8 * 252.6260504 + 2000}{\dfrac{1}{3} * 252.6260504^{-\dfrac{1}{3}} - 8} \\[5ex] $

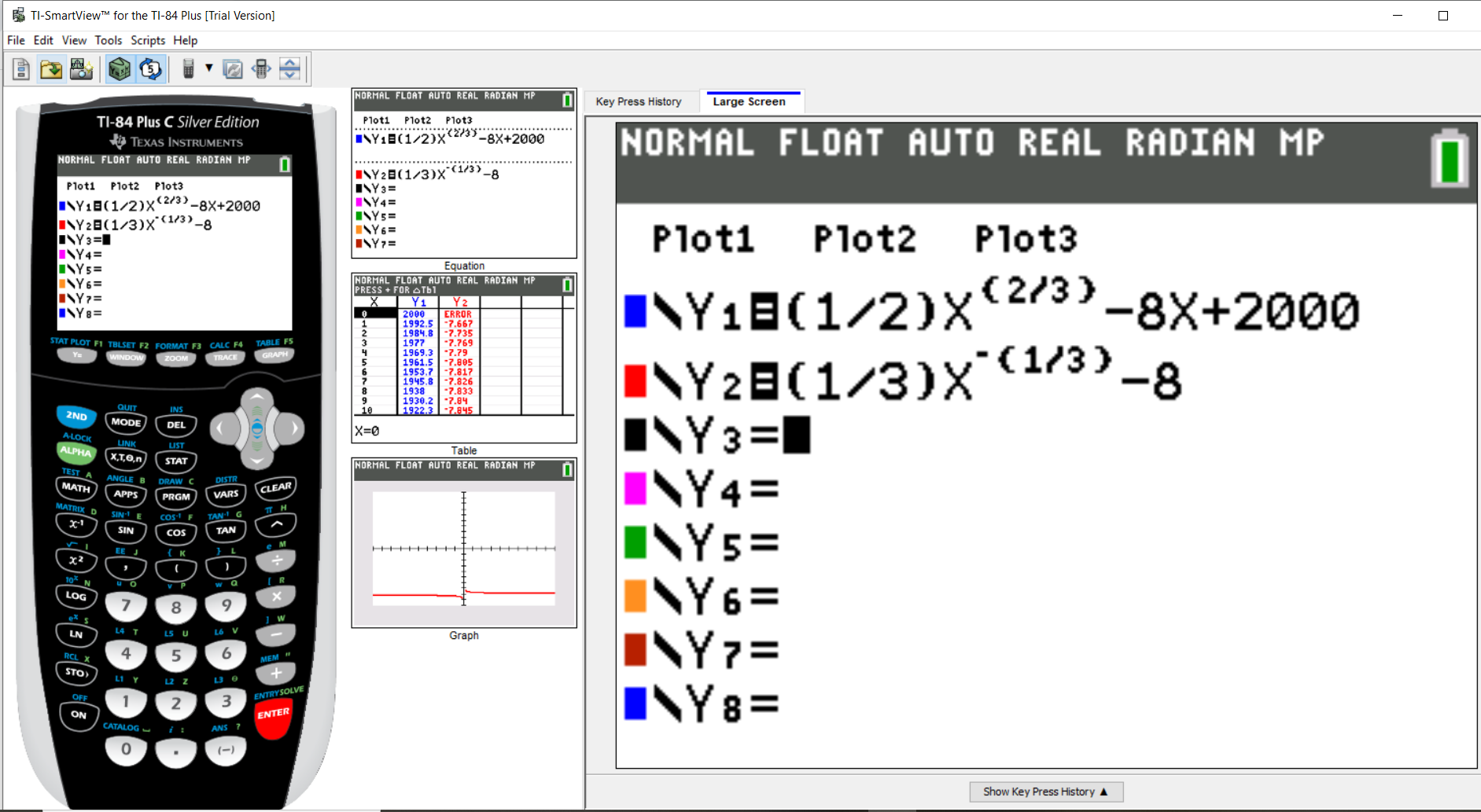
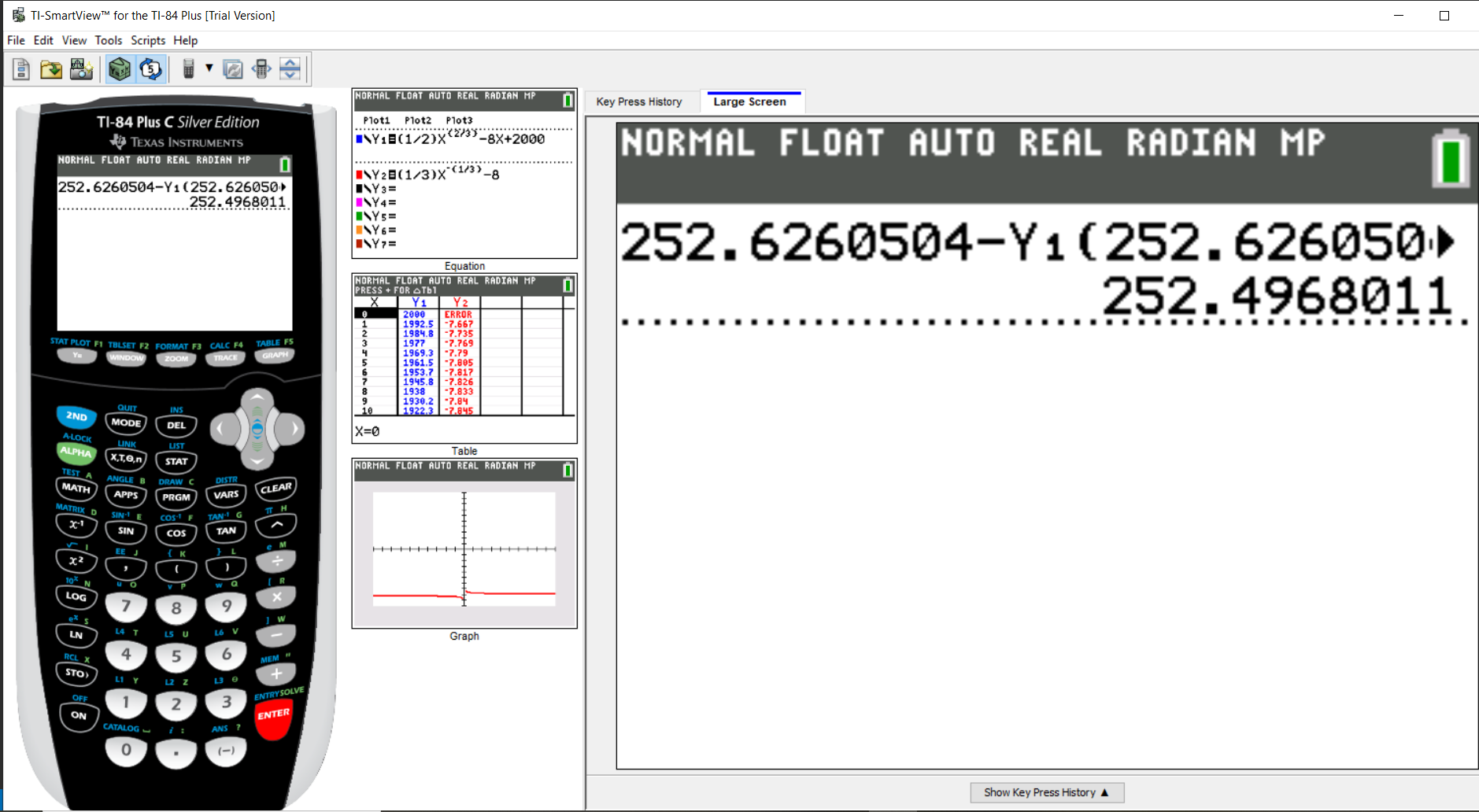
$ x_3 = 252.4968011 \\[3ex] $

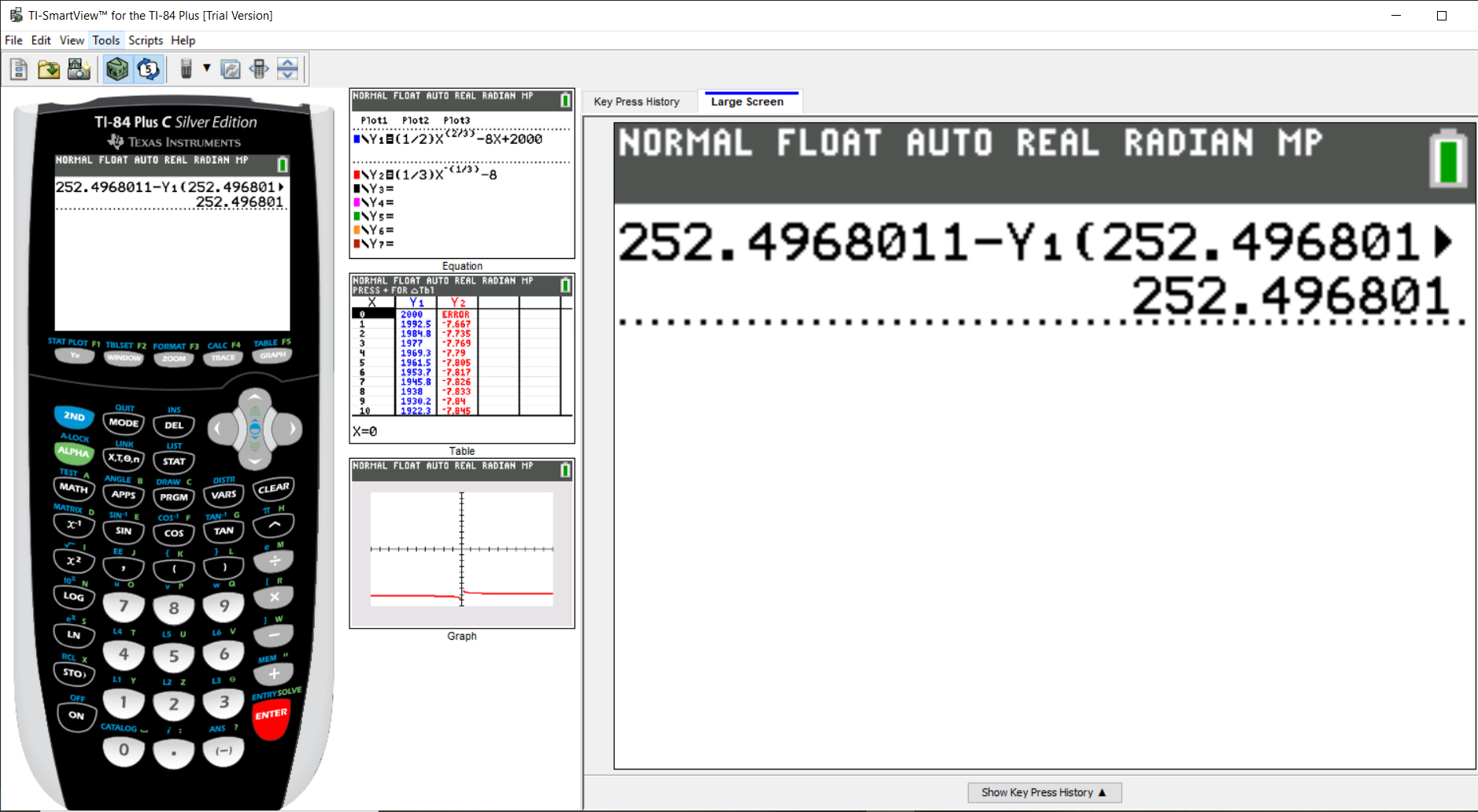
$ x_4 = 252.496801 \\[3ex] x_4 \approx x_3...STOP \\[3ex] \implies \\[3ex] x \approx 252 \\[3ex] $ The break-even point is approximately 252 books.

Top