Solved Examples: Integrals
(1.) Evaluate $\displaystyle\int -7dx$
Power Rule
$ \displaystyle\int -7dx \\[5ex] = \displaystyle\int -7 * 1 * dx \\[5ex] 1 = x^0 ...Law\:\:3...Exp \\[3ex] = \displaystyle\int -7x^0dx \\[5ex] = -7 \displaystyle\int x^0dx \\[5ex] = -7 * \dfrac{x^{0 + 1}}{0 + 1} + C \\[5ex] = -7 * \dfrac{x^1}{1} + C \\[5ex] = -7x + C $
Power Rule
$ \displaystyle\int -7dx \\[5ex] = \displaystyle\int -7 * 1 * dx \\[5ex] 1 = x^0 ...Law\:\:3...Exp \\[3ex] = \displaystyle\int -7x^0dx \\[5ex] = -7 \displaystyle\int x^0dx \\[5ex] = -7 * \dfrac{x^{0 + 1}}{0 + 1} + C \\[5ex] = -7 * \dfrac{x^1}{1} + C \\[5ex] = -7x + C $
(2.) JAMB Evaluate $\displaystyle\int_1^3 (x^2 - 1)dx$
$ A.\:\: -6\dfrac{2}{3} \\[5ex] B.\:\: 6\dfrac{2}{3} \\[5ex] C.\:\: \dfrac{2}{3} \\[5ex] D.\:\: -\dfrac{2}{3} \\[5ex] $
Power Rule
$ \displaystyle\int_1^3 (x^2 - 1)dx \\[5ex] \displaystyle (x^2 - 1)dx = \displaystyle\int x^2dx - \displaystyle\int 1dx \\[5ex] 1 = x^0 ...Law\:\:3...Exp \\[3ex] = \dfrac{x^{2 + 1}}{2 + 1} - \displaystyle\int x^0dx \\[5ex] = \dfrac{x^3}{3} - \dfrac{x^{0 + 1}}{0 + 1} + C \\[5ex] = \dfrac{x^3}{3} - x + C \\[5ex] \rightarrow \\[3ex] \displaystyle\int_1^3 (x^2 - 1)dx = \left[\dfrac{x^3}{3} - x\right]_1^3 \\[5ex] = \left(\dfrac{3^3}{3} - 3\right) - \left(\dfrac{1^3}{3} - 1\right) \\[5ex] = (9 - 3) - \left(\dfrac{1}{3} - \dfrac{3}{3}\right) \\[5ex] = 6 - \left(-\dfrac{2}{3}\right) \\[5ex] = 6 + \dfrac{2}{3} \\[5ex] = 6\dfrac{2}{3} $
$ A.\:\: -6\dfrac{2}{3} \\[5ex] B.\:\: 6\dfrac{2}{3} \\[5ex] C.\:\: \dfrac{2}{3} \\[5ex] D.\:\: -\dfrac{2}{3} \\[5ex] $
Power Rule
$ \displaystyle\int_1^3 (x^2 - 1)dx \\[5ex] \displaystyle (x^2 - 1)dx = \displaystyle\int x^2dx - \displaystyle\int 1dx \\[5ex] 1 = x^0 ...Law\:\:3...Exp \\[3ex] = \dfrac{x^{2 + 1}}{2 + 1} - \displaystyle\int x^0dx \\[5ex] = \dfrac{x^3}{3} - \dfrac{x^{0 + 1}}{0 + 1} + C \\[5ex] = \dfrac{x^3}{3} - x + C \\[5ex] \rightarrow \\[3ex] \displaystyle\int_1^3 (x^2 - 1)dx = \left[\dfrac{x^3}{3} - x\right]_1^3 \\[5ex] = \left(\dfrac{3^3}{3} - 3\right) - \left(\dfrac{1^3}{3} - 1\right) \\[5ex] = (9 - 3) - \left(\dfrac{1}{3} - \dfrac{3}{3}\right) \\[5ex] = 6 - \left(-\dfrac{2}{3}\right) \\[5ex] = 6 + \dfrac{2}{3} \\[5ex] = 6\dfrac{2}{3} $
(3.) Evaluate $\displaystyle\int (3^p + 7^p)dp$
Standard Integral
$ \displaystyle\int a^x dx = \dfrac{a^x}{\ln a} + C \\[5ex] \displaystyle\int (3^p + 7^p)dp = \displaystyle\int 3^pdp + \displaystyle\int 7^pdp \\[5ex] \displaystyle\int 3^p dx = \dfrac{3^p}{\ln 3} \\[5ex] \displaystyle\int 7^p dx = \dfrac{7^p}{\ln 7} \\[5ex] \rightarrow \\[3ex] \displaystyle\int (3^p + 7^p)dp = \dfrac{3^p}{\ln 3} + \dfrac{7^p}{\ln 7} + C $
Standard Integral
$ \displaystyle\int a^x dx = \dfrac{a^x}{\ln a} + C \\[5ex] \displaystyle\int (3^p + 7^p)dp = \displaystyle\int 3^pdp + \displaystyle\int 7^pdp \\[5ex] \displaystyle\int 3^p dx = \dfrac{3^p}{\ln 3} \\[5ex] \displaystyle\int 7^p dx = \dfrac{7^p}{\ln 7} \\[5ex] \rightarrow \\[3ex] \displaystyle\int (3^p + 7^p)dp = \dfrac{3^p}{\ln 3} + \dfrac{7^p}{\ln 7} + C $
(4.) Evaluate $\displaystyle\int (v^{-2} + 8v^{-1})dv$
Power Rule
$ \displaystyle\int (v^{-2} + 8v^{-1})dv \\[5ex] = \displaystyle\int v^{-2}dv + \displaystyle\int 8v^{-1}dv \\[5ex] = \dfrac{v^{-2 + 1}}{-2 + 1} + 8 * \displaystyle\int v^{-1}dv \\[5ex] = \dfrac{v^{-1}}{-1} + 8 * \ln v + C \\[5ex] = -v^{-1} + 8\ln v + C \\[5ex] = -\dfrac{1}{v} + 8\ln v + C \\[5ex] = 8\ln v - \dfrac{1}{v} + C $
Power Rule
$ \displaystyle\int (v^{-2} + 8v^{-1})dv \\[5ex] = \displaystyle\int v^{-2}dv + \displaystyle\int 8v^{-1}dv \\[5ex] = \dfrac{v^{-2 + 1}}{-2 + 1} + 8 * \displaystyle\int v^{-1}dv \\[5ex] = \dfrac{v^{-1}}{-1} + 8 * \ln v + C \\[5ex] = -v^{-1} + 8\ln v + C \\[5ex] = -\dfrac{1}{v} + 8\ln v + C \\[5ex] = 8\ln v - \dfrac{1}{v} + C $
(5.)
1st: We shall find the slope of the tangent to the curve at at x = 2.
This is the derivative of the function at x = 2.
2nd: We shall determine the slope of the normal to the curve
The normal to the curve is perpendicular to the tangent to the curve
Hence, the product of the two slopes (product of the slope of the tangent and the slope of the normal) is −1
3rd: We shall determine the point (x1, y1) on the curve
We already know the x-coordinate, but we shall find the y-coordinate
4th: We shall use the Point-Slope Form to determine the equation of the normal to the curve.
$ y = 7x - 5x^2 \\[3ex] \underline{\text{Slope of the tangent to the curve}}, m_T \\[3ex] \dfrac{dy}{dx} = 7 - 10x \\[3ex] @\;x = 2 \\[3ex] m_T = \left.\dfrac{dy}{dx}\right|_{x = 2} \\[5ex] = 7 - 10(2) \\[3ex] = 7 - 20 \\[3ex] = -13 \\[5ex] \underline{\text{Slope of the normal to the curve}}, m_N \\[3ex] m_N * m_T = -1 \\[3ex] m_N * 13 = -1 \\[3ex] m_N = \dfrac{-1}{-13} \\[5ex] m_N = \dfrac{1}{13} \\[5ex] \underline{\text{Point on the curve}}, (x_1, y_1) \\[3ex] y = 7x - 5x^2 \\[3ex] @\;x = 2 \\[3ex] y = 7(2) - 5(2)^2 \\[3ex] = 14 - 5(4) \\[3ex] = 14 - 20 \\[3ex] = -6 \\[3ex] (x_1, y_1) = (2, -6) \\[5ex] \underline{\text{Equation of the normal to the curve}} \\[3ex] \text{Point – Slope Form} \\[3ex] y - y_1 = m_N(x - x_1) \\[4ex] y - -6 = \dfrac{1}{13}(x - 2) \\[5ex] y + 6 = \dfrac{1}{13}x - \dfrac{2}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - 6 \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - \dfrac{78}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{80}{13} \\[5ex] LCD = 13 \\[3ex] \text{Multiply each term by 13} \\[3ex] 13y = 13\left(\dfrac{1}{13}x\right) - 13\left(\dfrac{80}{13}\right) \\[5ex] 13y = x - 80 \\[3ex] 13y - x + 80 = 0 $
1st: We shall find the slope of the tangent to the curve at at x = 2.
This is the derivative of the function at x = 2.
2nd: We shall determine the slope of the normal to the curve
The normal to the curve is perpendicular to the tangent to the curve
Hence, the product of the two slopes (product of the slope of the tangent and the slope of the normal) is −1
3rd: We shall determine the point (x1, y1) on the curve
We already know the x-coordinate, but we shall find the y-coordinate
4th: We shall use the Point-Slope Form to determine the equation of the normal to the curve.
$ y = 7x - 5x^2 \\[3ex] \underline{\text{Slope of the tangent to the curve}}, m_T \\[3ex] \dfrac{dy}{dx} = 7 - 10x \\[3ex] @\;x = 2 \\[3ex] m_T = \left.\dfrac{dy}{dx}\right|_{x = 2} \\[5ex] = 7 - 10(2) \\[3ex] = 7 - 20 \\[3ex] = -13 \\[5ex] \underline{\text{Slope of the normal to the curve}}, m_N \\[3ex] m_N * m_T = -1 \\[3ex] m_N * 13 = -1 \\[3ex] m_N = \dfrac{-1}{-13} \\[5ex] m_N = \dfrac{1}{13} \\[5ex] \underline{\text{Point on the curve}}, (x_1, y_1) \\[3ex] y = 7x - 5x^2 \\[3ex] @\;x = 2 \\[3ex] y = 7(2) - 5(2)^2 \\[3ex] = 14 - 5(4) \\[3ex] = 14 - 20 \\[3ex] = -6 \\[3ex] (x_1, y_1) = (2, -6) \\[5ex] \underline{\text{Equation of the normal to the curve}} \\[3ex] \text{Point – Slope Form} \\[3ex] y - y_1 = m_N(x - x_1) \\[4ex] y - -6 = \dfrac{1}{13}(x - 2) \\[5ex] y + 6 = \dfrac{1}{13}x - \dfrac{2}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - 6 \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - \dfrac{78}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{80}{13} \\[5ex] LCD = 13 \\[3ex] \text{Multiply each term by 13} \\[3ex] 13y = 13\left(\dfrac{1}{13}x\right) - 13\left(\dfrac{80}{13}\right) \\[5ex] 13y = x - 80 \\[3ex] 13y - x + 80 = 0 $
(6.) Determine the antiderivative of $\cot x$
Integration by Algebraic Substitution
$ \displaystyle\int \cot xdx \\[5ex] \cot x = \dfrac{\cos x}{\sin x}...Quotient\:\:Identity \\[5ex] Let\:\: p = \sin x \\[3ex] \dfrac{dp}{dx} = \cos x \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{\cos x} \\[5ex] dx = \dfrac{dp}{\cos x} \\[5ex] \rightarrow \\[3ex] \displaystyle\int \cot xdx = \displaystyle\int \dfrac{\cos x}{\sin x} dx \\[5ex] = \displaystyle\int \dfrac{\cos x}{p} * \dfrac{dp}{\cos x} \\[5ex] = \displaystyle\int \dfrac{dp}{p} \\[5ex] = \ln p + C \\[3ex] = \ln \sin x + C $
Integration by Algebraic Substitution
$ \displaystyle\int \cot xdx \\[5ex] \cot x = \dfrac{\cos x}{\sin x}...Quotient\:\:Identity \\[5ex] Let\:\: p = \sin x \\[3ex] \dfrac{dp}{dx} = \cos x \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{\cos x} \\[5ex] dx = \dfrac{dp}{\cos x} \\[5ex] \rightarrow \\[3ex] \displaystyle\int \cot xdx = \displaystyle\int \dfrac{\cos x}{\sin x} dx \\[5ex] = \displaystyle\int \dfrac{\cos x}{p} * \dfrac{dp}{\cos x} \\[5ex] = \displaystyle\int \dfrac{dp}{p} \\[5ex] = \ln p + C \\[3ex] = \ln \sin x + C $
(7.) JAMB Evaluate $\displaystyle\int \sin 3xdx$
$ A.\:\: -\dfrac{1}{3}\cos 3x + c \\[5ex] B.\:\: \dfrac{1}{3}\cos 3x + c \\[5ex] C.\:\: \dfrac{2}{3}\cos 3x + c \\[5ex] C.\:\: -\dfrac{2}{3}\cos 3x + c \\[5ex] $
Integration by Algebraic Substitution
$ \displaystyle\int \sin 3xdx \\[5ex] Let\:\: p = 3x \\[3ex] \dfrac{dp}{dx} = 3 \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{3} \\[5ex] dx = \dfrac{dp}{3} \\[5ex] \rightarrow \\[3ex] \displaystyle\int \sin 3xdx = \displaystyle\int \sin p * \dfrac{dp}{3} \\[5ex] = \dfrac{1}{3} * \displaystyle\int \sin pdp \\[5ex] = \dfrac{1}{3} * -\cos p + C \\[5ex] = \dfrac{1}{3} * - \cos 3x + C \\[3ex] = -\dfrac{1}{3}\cos 3x + c $
$ A.\:\: -\dfrac{1}{3}\cos 3x + c \\[5ex] B.\:\: \dfrac{1}{3}\cos 3x + c \\[5ex] C.\:\: \dfrac{2}{3}\cos 3x + c \\[5ex] C.\:\: -\dfrac{2}{3}\cos 3x + c \\[5ex] $
Integration by Algebraic Substitution
$ \displaystyle\int \sin 3xdx \\[5ex] Let\:\: p = 3x \\[3ex] \dfrac{dp}{dx} = 3 \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{3} \\[5ex] dx = \dfrac{dp}{3} \\[5ex] \rightarrow \\[3ex] \displaystyle\int \sin 3xdx = \displaystyle\int \sin p * \dfrac{dp}{3} \\[5ex] = \dfrac{1}{3} * \displaystyle\int \sin pdp \\[5ex] = \dfrac{1}{3} * -\cos p + C \\[5ex] = \dfrac{1}{3} * - \cos 3x + C \\[3ex] = -\dfrac{1}{3}\cos 3x + c $
(8.) Evaluate $\displaystyle\int \sqrt{2 + \sqrt{x}} dx$
Integration by Algebraic Substitution
$ \displaystyle\int \sqrt{2 + \sqrt{x}} dx \\[3ex] Let\:\: p = 2 + \sqrt{x} \\[3ex] \dfrac{dp}{dx} = \dfrac{1}{2\sqrt{x}} \\[5ex] \dfrac{dx}{dp} = 2\sqrt{x} \\[5ex] dx = 2\sqrt{x}dp \\[3ex] \rightarrow \\[3ex] \displaystyle\int \sqrt{2 + \sqrt{x}} dx = \displaystyle\int \sqrt{p} * 2\sqrt{x} dp \\[3ex] = 2\displaystyle\int \sqrt{p} * \sqrt{x} dp \\[3ex] p = 2 + \sqrt{x} \rightarrow \sqrt{x} = p - 2 \\[3ex] = 2 * \displaystyle\int \sqrt{p}(p - 2) dp \\[3ex] \displaystyle\int \sqrt{p}(p - 2) dp = \displaystyle\int p\sqrt{p}dp - \displaystyle\int 2\sqrt{p}dp \\[3ex] \displaystyle\int p\sqrt{p}dp = \displaystyle\int p^1 * p^{\dfrac{1}{2}}dp = \displaystyle\int p^{1 + \dfrac{1}{2}}dp = \displaystyle\int p^{\dfrac{3}{2}}dp \\[5ex] \displaystyle\int p\sqrt{p}dp = \dfrac{p^{\dfrac{3}{2} + 1}}{\dfrac{3}{2} + 1} \\[7ex] \displaystyle\int p\sqrt{p}dp = p^{\dfrac{5}{2}} \div \dfrac{5}{2} \\[5ex] \displaystyle\int p\sqrt{p}dp = p^{\dfrac{5}{2}} * \dfrac{2}{5} \\[5ex] p^{\dfrac{5}{2}} = (\sqrt{p})^5 = (\sqrt{p})^4 * \sqrt{p} = \left(p^{\dfrac{1}{2}}\right)^4 * \sqrt{p} = p^2\sqrt{p} \\[5ex] \displaystyle\int p\sqrt{p}dp = \dfrac{2p^2}{5} \\[5ex] \displaystyle\int 2\sqrt{p}dp = 2\displaystyle\int \sqrt{p}dp \\[3ex] \displaystyle\int \sqrt{p}dp = \dfrac{p^{\dfrac{1}{2} + 1}}{\dfrac{1}{2} + 1} \\[7ex] \displaystyle\int \sqrt{p}dp = p^{\dfrac{3}{2}} \div \dfrac{3}{2} \\[5ex] \displaystyle\int \sqrt{p}dp = p^{\dfrac{3}{2}} * \dfrac{2}{3} \\[5ex] p^{\dfrac{3}{2}} = (\sqrt{p})^3 = (\sqrt{p})^2 * \sqrt{p} = \left(p^{\dfrac{1}{2}}\right)^2 * \sqrt{p} = p\sqrt{p} \\[5ex] \displaystyle\int 2\sqrt{p}dp = \dfrac{2p\sqrt{p}}{3} \\[5ex] \rightarrow \\[3ex] displaystyle\int \sqrt{p}(p - 2) dp = \dfrac{2p^2\sqrt{p}}{5} - \dfrac{2p\sqrt{p}}{3} \\[5ex] = 2p\sqrt{p}\left(\dfrac{p}{5} - \dfrac{1}{3}\right) \\[5ex] = 2p\sqrt{p}\left(\dfrac{3p}{15} - \dfrac{5}{15}\right) \\[5ex] = 2p\sqrt{p}\left(\dfrac{3p - 5}{15}\right) \\[5ex] \rightarrow \\[3ex] 2 * \displaystyle\int \sqrt{p}(p - 2) dp = 2 * 2p\sqrt{p}\left(\dfrac{3p - 5}{15}\right) \\[5ex] = 4p\sqrt{p}\left(\dfrac{3p - 5}{15}\right) \\[5ex] Substitute\:\:back \\[3ex] = 4(2 + \sqrt{x})\sqrt{2 + \sqrt{x}}\left(\dfrac{3(2 + \sqrt{x}) - 5}{15}\right) \\[5ex] \dfrac{3(2 + \sqrt{x}) - 5}{15} = \dfrac{6 + 3\sqrt{x} - 5}{15} = \dfrac{1 + 3\sqrt{x}}{15} \\[5ex] \rightarrow \\[3ex] displaystyle\int \sqrt{2 + \sqrt{x}} dx = 4(2 + \sqrt{x})\left(\sqrt{2 + \sqrt{x}}\right)\left(\dfrac{1 + 3\sqrt{x}}{15}\right) \\[5ex] \therefore \displaystyle\int \sqrt{2 + \sqrt{x}} dx = \dfrac{4}{15}(2 + \sqrt{x})(1 + 3\sqrt{x})\left(\sqrt{2 + \sqrt{x}}\right) + C $
Integration by Algebraic Substitution
$ \displaystyle\int \sqrt{2 + \sqrt{x}} dx \\[3ex] Let\:\: p = 2 + \sqrt{x} \\[3ex] \dfrac{dp}{dx} = \dfrac{1}{2\sqrt{x}} \\[5ex] \dfrac{dx}{dp} = 2\sqrt{x} \\[5ex] dx = 2\sqrt{x}dp \\[3ex] \rightarrow \\[3ex] \displaystyle\int \sqrt{2 + \sqrt{x}} dx = \displaystyle\int \sqrt{p} * 2\sqrt{x} dp \\[3ex] = 2\displaystyle\int \sqrt{p} * \sqrt{x} dp \\[3ex] p = 2 + \sqrt{x} \rightarrow \sqrt{x} = p - 2 \\[3ex] = 2 * \displaystyle\int \sqrt{p}(p - 2) dp \\[3ex] \displaystyle\int \sqrt{p}(p - 2) dp = \displaystyle\int p\sqrt{p}dp - \displaystyle\int 2\sqrt{p}dp \\[3ex] \displaystyle\int p\sqrt{p}dp = \displaystyle\int p^1 * p^{\dfrac{1}{2}}dp = \displaystyle\int p^{1 + \dfrac{1}{2}}dp = \displaystyle\int p^{\dfrac{3}{2}}dp \\[5ex] \displaystyle\int p\sqrt{p}dp = \dfrac{p^{\dfrac{3}{2} + 1}}{\dfrac{3}{2} + 1} \\[7ex] \displaystyle\int p\sqrt{p}dp = p^{\dfrac{5}{2}} \div \dfrac{5}{2} \\[5ex] \displaystyle\int p\sqrt{p}dp = p^{\dfrac{5}{2}} * \dfrac{2}{5} \\[5ex] p^{\dfrac{5}{2}} = (\sqrt{p})^5 = (\sqrt{p})^4 * \sqrt{p} = \left(p^{\dfrac{1}{2}}\right)^4 * \sqrt{p} = p^2\sqrt{p} \\[5ex] \displaystyle\int p\sqrt{p}dp = \dfrac{2p^2}{5} \\[5ex] \displaystyle\int 2\sqrt{p}dp = 2\displaystyle\int \sqrt{p}dp \\[3ex] \displaystyle\int \sqrt{p}dp = \dfrac{p^{\dfrac{1}{2} + 1}}{\dfrac{1}{2} + 1} \\[7ex] \displaystyle\int \sqrt{p}dp = p^{\dfrac{3}{2}} \div \dfrac{3}{2} \\[5ex] \displaystyle\int \sqrt{p}dp = p^{\dfrac{3}{2}} * \dfrac{2}{3} \\[5ex] p^{\dfrac{3}{2}} = (\sqrt{p})^3 = (\sqrt{p})^2 * \sqrt{p} = \left(p^{\dfrac{1}{2}}\right)^2 * \sqrt{p} = p\sqrt{p} \\[5ex] \displaystyle\int 2\sqrt{p}dp = \dfrac{2p\sqrt{p}}{3} \\[5ex] \rightarrow \\[3ex] displaystyle\int \sqrt{p}(p - 2) dp = \dfrac{2p^2\sqrt{p}}{5} - \dfrac{2p\sqrt{p}}{3} \\[5ex] = 2p\sqrt{p}\left(\dfrac{p}{5} - \dfrac{1}{3}\right) \\[5ex] = 2p\sqrt{p}\left(\dfrac{3p}{15} - \dfrac{5}{15}\right) \\[5ex] = 2p\sqrt{p}\left(\dfrac{3p - 5}{15}\right) \\[5ex] \rightarrow \\[3ex] 2 * \displaystyle\int \sqrt{p}(p - 2) dp = 2 * 2p\sqrt{p}\left(\dfrac{3p - 5}{15}\right) \\[5ex] = 4p\sqrt{p}\left(\dfrac{3p - 5}{15}\right) \\[5ex] Substitute\:\:back \\[3ex] = 4(2 + \sqrt{x})\sqrt{2 + \sqrt{x}}\left(\dfrac{3(2 + \sqrt{x}) - 5}{15}\right) \\[5ex] \dfrac{3(2 + \sqrt{x}) - 5}{15} = \dfrac{6 + 3\sqrt{x} - 5}{15} = \dfrac{1 + 3\sqrt{x}}{15} \\[5ex] \rightarrow \\[3ex] displaystyle\int \sqrt{2 + \sqrt{x}} dx = 4(2 + \sqrt{x})\left(\sqrt{2 + \sqrt{x}}\right)\left(\dfrac{1 + 3\sqrt{x}}{15}\right) \\[5ex] \therefore \displaystyle\int \sqrt{2 + \sqrt{x}} dx = \dfrac{4}{15}(2 + \sqrt{x})(1 + 3\sqrt{x})\left(\sqrt{2 + \sqrt{x}}\right) + C $
(9.) Find the integral of $\tan x$
Integration by Algebraic Substitution
$ \displaystyle\int \tan xdx \\[5ex] \tan x = \dfrac{\sin x}{\cos x}...Quotient\:\:Identity \\[5ex] Let\:\: p = \cos x \\[3ex] \dfrac{dp}{dx} = -\sin x \\[5ex] \dfrac{dx}{dp} = -\dfrac{1}{\sin x} \\[5ex] dx = -\dfrac{dp}{\sin x} \\[5ex] \rightarrow \\[3ex] \displaystyle\int \tan xdx = \displaystyle\int \dfrac{\sin x}{\cos x} dx \\[5ex] = \displaystyle\int \dfrac{\sin x}{p} * -\dfrac{dp}{\sin x} \\[5ex] = \displaystyle\int -\dfrac{dp}{p} \\[5ex] = -\ln p + C \\[3ex] = -\ln \cos x + C $
Integration by Algebraic Substitution
$ \displaystyle\int \tan xdx \\[5ex] \tan x = \dfrac{\sin x}{\cos x}...Quotient\:\:Identity \\[5ex] Let\:\: p = \cos x \\[3ex] \dfrac{dp}{dx} = -\sin x \\[5ex] \dfrac{dx}{dp} = -\dfrac{1}{\sin x} \\[5ex] dx = -\dfrac{dp}{\sin x} \\[5ex] \rightarrow \\[3ex] \displaystyle\int \tan xdx = \displaystyle\int \dfrac{\sin x}{\cos x} dx \\[5ex] = \displaystyle\int \dfrac{\sin x}{p} * -\dfrac{dp}{\sin x} \\[5ex] = \displaystyle\int -\dfrac{dp}{p} \\[5ex] = -\ln p + C \\[3ex] = -\ln \cos x + C $
(10.) Evaluate $\displaystyle\int_1^e \dfrac{\ln x}{x} dx$
$ \displaystyle\int_1^e \dfrac{\ln x}{x} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = \ln x \\[3ex] \dfrac{dp}{dx} = \dfrac{1}{x} \\[5ex] \dfrac{dx}{dp} = x \\[5ex] dx = xdp \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{p}{x} * x dp \\[5ex] = \displaystyle\int p dp \\[3ex] = \dfrac{p^2}{2} \\[5ex] = \dfrac{(\ln x)^2}{2} \\[5ex] \left[\dfrac{(\ln x)^2}{2}\right]_1^e \\[5ex] = \dfrac{1}{2}[(\ln x)^2]_1^e \\[5ex] = \dfrac{1}{2}[(\ln e)^2 - (\ln 1)^2] \\[5ex] = \dfrac{1}{2}[1^2 - 0^2] \\[5ex] = \dfrac{1}{2}[1 - 0] \\[5ex] = \dfrac{1}{2} $

$ \displaystyle\int_1^e \dfrac{\ln x}{x} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = \ln x \\[3ex] \dfrac{dp}{dx} = \dfrac{1}{x} \\[5ex] \dfrac{dx}{dp} = x \\[5ex] dx = xdp \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{p}{x} * x dp \\[5ex] = \displaystyle\int p dp \\[3ex] = \dfrac{p^2}{2} \\[5ex] = \dfrac{(\ln x)^2}{2} \\[5ex] \left[\dfrac{(\ln x)^2}{2}\right]_1^e \\[5ex] = \dfrac{1}{2}[(\ln x)^2]_1^e \\[5ex] = \dfrac{1}{2}[(\ln e)^2 - (\ln 1)^2] \\[5ex] = \dfrac{1}{2}[1^2 - 0^2] \\[5ex] = \dfrac{1}{2}[1 - 0] \\[5ex] = \dfrac{1}{2} $

(11.) WASSCE:FM Evaluate $\displaystyle\int_0^1 \dfrac{3 - 3x^2}{x + 1}dx$
$ A.\:\: 1\dfrac{1}{3} \\[5ex] B.\:\: 1\dfrac{1}{2} \\[5ex] C.\:\: 3 \\[3ex] D.\:\: 4\dfrac{1}{2} \\[5ex] $
Power Rule
$ \displaystyle\int_0^1 \dfrac{3 - 3x^2}{x + 1}dx \\[5ex] 3 - 3x^2 = 3(1 - x^2) \\[3ex] 1 - x^2 = 1^2 - x^2 = (1 + x)(1 - x)...Difference\:\:of\:\:Two\:\:Squares \\[3ex] 3 - 3x^2 = 3(1 + x)(1 - x) = 3(x + 1)(1 - x) \\[3ex] \rightarrow \\[3ex] \dfrac{3 - 3x^2}{x + 1} = \dfrac{3(x + 1)(1 - x)}{x + 1} = 3(1 - x) = 3 - 3x \\[5ex] \rightarrow \\[3ex] \displaystyle\int (3 - 3x)dx = \displaystyle\int 3dx - \displaystyle\int 3xdx \\[5ex] \displaystyle\int 3dx = 3x \\[5ex] \displaystyle\int 3xdx = 3 * \dfrac{x^{1 + 1}}{1 + 1} = \dfrac{3x^2}{2} \\[5ex] \rightarrow \\[3ex] \displaystyle\int_0^1 \dfrac{3 - 3x^2}{x + 1}dx = \left[3x - \dfrac{3x^2}{2}\right]_0^1 \\[5ex] = \left[3(1) - \dfrac{3(1)^2}{2}\right] - \left[3(0) - \dfrac{3(0)^2}{2}\right] \\[5ex] = \left[3 - \dfrac{3(1)}{2}\right] - \left[0 - \dfrac{3(0)}{2}\right] \\[5ex] = \left(3 - \dfrac{3}{2}\right) - \left(0 - \dfrac{0}{2}\right) \\[5ex] = \left(\dfrac{6}{2} - \dfrac{3}{2}\right) - (0 - 0) \\[5ex] = \dfrac{6 - 3}{2} - 0 \\[5ex] = \dfrac{3}{2} \\[5ex] = 1\dfrac{1}{2} $
$ A.\:\: 1\dfrac{1}{3} \\[5ex] B.\:\: 1\dfrac{1}{2} \\[5ex] C.\:\: 3 \\[3ex] D.\:\: 4\dfrac{1}{2} \\[5ex] $
Power Rule
$ \displaystyle\int_0^1 \dfrac{3 - 3x^2}{x + 1}dx \\[5ex] 3 - 3x^2 = 3(1 - x^2) \\[3ex] 1 - x^2 = 1^2 - x^2 = (1 + x)(1 - x)...Difference\:\:of\:\:Two\:\:Squares \\[3ex] 3 - 3x^2 = 3(1 + x)(1 - x) = 3(x + 1)(1 - x) \\[3ex] \rightarrow \\[3ex] \dfrac{3 - 3x^2}{x + 1} = \dfrac{3(x + 1)(1 - x)}{x + 1} = 3(1 - x) = 3 - 3x \\[5ex] \rightarrow \\[3ex] \displaystyle\int (3 - 3x)dx = \displaystyle\int 3dx - \displaystyle\int 3xdx \\[5ex] \displaystyle\int 3dx = 3x \\[5ex] \displaystyle\int 3xdx = 3 * \dfrac{x^{1 + 1}}{1 + 1} = \dfrac{3x^2}{2} \\[5ex] \rightarrow \\[3ex] \displaystyle\int_0^1 \dfrac{3 - 3x^2}{x + 1}dx = \left[3x - \dfrac{3x^2}{2}\right]_0^1 \\[5ex] = \left[3(1) - \dfrac{3(1)^2}{2}\right] - \left[3(0) - \dfrac{3(0)^2}{2}\right] \\[5ex] = \left[3 - \dfrac{3(1)}{2}\right] - \left[0 - \dfrac{3(0)}{2}\right] \\[5ex] = \left(3 - \dfrac{3}{2}\right) - \left(0 - \dfrac{0}{2}\right) \\[5ex] = \left(\dfrac{6}{2} - \dfrac{3}{2}\right) - (0 - 0) \\[5ex] = \dfrac{6 - 3}{2} - 0 \\[5ex] = \dfrac{3}{2} \\[5ex] = 1\dfrac{1}{2} $
(12.) ATAR (a) Given that $\dfrac{2}{(x + 1)(x - 1)} = \dfrac{a}{x - 1} + \dfrac{b}{x + 1}$
determine the values for a and b
(b) Hence determine $\displaystyle\int \dfrac{1}{x^2 - 1}dx$
Numerator: cannot be simplified further
Form: Proper Fraction: Non-repeated Linear Factors at the Denominator
$ \dfrac{2}{(x + 1)(x - 1)} \\[5ex] = \dfrac{a}{x - 1} + \dfrac{b}{x + 1} \\[5ex] = \dfrac{a(x + 1) + b(x - 1)}{(x - 1)(x + 1)} \\[5ex] = \dfrac{ax + a + bx - b}{(x - 1)(x + 1)} \\[5ex] = \dfrac{ax + bx + a - b}{(x - 1)(x + 1)} \\[5ex] $ Denominators are the same
Equate the numerators
$ 2 = ax + bx + a - b \\[3ex] ax + bx + a - b = 2 \\[3ex] ax + bx + a - b = 0x + 2 \\[3ex] \implies \\[3ex] a + b = 0 ...eqn.(1) \\[3ex] a - b = 2 ...eqn.(2) \\[3ex] eqn.(1) + eqn.(2) \implies \\[3ex] 2a = 2 \\[3ex] a = \dfrac{2}{2} \\[5ex] a = 1 \\[3ex] eqn.(1) - eqn.(2) \implies \\[3ex] 2b = -2 \\[3ex] b = -\dfrac{2}{2} \\[5ex] b = -1 \\[3ex] \therefore \dfrac{2}{(x + 1)(x - 1)} = \dfrac{1}{x - 1} + \dfrac{-1}{x + 1} \\[5ex] \dfrac{2}{(x - 1)(x + 1)} = \dfrac{1}{x - 1} - \dfrac{1}{x + 1} \\[5ex] \underline{Check} \\[3ex] \underline{RHS} \\[3ex] \dfrac{1}{x - 1} - \dfrac{1}{x + 1} \\[5ex] = \dfrac{1(x + 1) - 1(x - 1)}{(x - 1)(x + 1)} \\[5ex] = \dfrac{x + 1 - x + 1}{(x - 1)(x + 1)} \\[5ex] = \dfrac{2}{(x - 1)(x + 1)} \\[5ex] = \dfrac{2}{(x + 1)(x - 1)} \\[5ex] = LHS \\[3ex] $ Integration by Partial Fractions
(b) Because of the word, "Hence"; we are expected to use the result we got from Part (a) to solve Part (b)
However, the partial fraction we did in (a) is slightly different from the integral in (b)
So, we need to make some modifications in order to solve it.
$ \displaystyle\int \dfrac{1}{x^2 - 1}dx \\[5ex] \underline{Denominator} \\[3ex] x^2 - 1 = (x + 1)(x - 1) ...Difference\;\;of\;\;Two\;\;Squares \\[3ex] \displaystyle\int \dfrac{1}{x^2 - 1}dx \\[5ex] = \displaystyle\int \dfrac{1}{(x + 1)(x - 1)} dx \\[5ex] = \dfrac{1}{2} * \displaystyle\int \dfrac{2}{(x + 1)(x - 1)} dx \\[5ex] = \dfrac{1}{2} * \left[\displaystyle\int \left(\dfrac{1}{x - 1} - \dfrac{1}{x + 1}\right) dx\right] \\[5ex] = \dfrac{1}{2} * \left[\displaystyle\int \dfrac{1}{x - 1}dx - \displaystyle\int \dfrac{1}{x + 1}dx\right] \\[5ex] = \dfrac{1}{2}[\ln|x - 1| - \ln|x + 1|] + C \\[5ex] = \dfrac{1}{2}\ln\dfrac{|x - 1|}{|x + 1|} + C $
determine the values for a and b
(b) Hence determine $\displaystyle\int \dfrac{1}{x^2 - 1}dx$
Numerator: cannot be simplified further
Form: Proper Fraction: Non-repeated Linear Factors at the Denominator
$ \dfrac{2}{(x + 1)(x - 1)} \\[5ex] = \dfrac{a}{x - 1} + \dfrac{b}{x + 1} \\[5ex] = \dfrac{a(x + 1) + b(x - 1)}{(x - 1)(x + 1)} \\[5ex] = \dfrac{ax + a + bx - b}{(x - 1)(x + 1)} \\[5ex] = \dfrac{ax + bx + a - b}{(x - 1)(x + 1)} \\[5ex] $ Denominators are the same
Equate the numerators
$ 2 = ax + bx + a - b \\[3ex] ax + bx + a - b = 2 \\[3ex] ax + bx + a - b = 0x + 2 \\[3ex] \implies \\[3ex] a + b = 0 ...eqn.(1) \\[3ex] a - b = 2 ...eqn.(2) \\[3ex] eqn.(1) + eqn.(2) \implies \\[3ex] 2a = 2 \\[3ex] a = \dfrac{2}{2} \\[5ex] a = 1 \\[3ex] eqn.(1) - eqn.(2) \implies \\[3ex] 2b = -2 \\[3ex] b = -\dfrac{2}{2} \\[5ex] b = -1 \\[3ex] \therefore \dfrac{2}{(x + 1)(x - 1)} = \dfrac{1}{x - 1} + \dfrac{-1}{x + 1} \\[5ex] \dfrac{2}{(x - 1)(x + 1)} = \dfrac{1}{x - 1} - \dfrac{1}{x + 1} \\[5ex] \underline{Check} \\[3ex] \underline{RHS} \\[3ex] \dfrac{1}{x - 1} - \dfrac{1}{x + 1} \\[5ex] = \dfrac{1(x + 1) - 1(x - 1)}{(x - 1)(x + 1)} \\[5ex] = \dfrac{x + 1 - x + 1}{(x - 1)(x + 1)} \\[5ex] = \dfrac{2}{(x - 1)(x + 1)} \\[5ex] = \dfrac{2}{(x + 1)(x - 1)} \\[5ex] = LHS \\[3ex] $ Integration by Partial Fractions
(b) Because of the word, "Hence"; we are expected to use the result we got from Part (a) to solve Part (b)
However, the partial fraction we did in (a) is slightly different from the integral in (b)
So, we need to make some modifications in order to solve it.
$ \displaystyle\int \dfrac{1}{x^2 - 1}dx \\[5ex] \underline{Denominator} \\[3ex] x^2 - 1 = (x + 1)(x - 1) ...Difference\;\;of\;\;Two\;\;Squares \\[3ex] \displaystyle\int \dfrac{1}{x^2 - 1}dx \\[5ex] = \displaystyle\int \dfrac{1}{(x + 1)(x - 1)} dx \\[5ex] = \dfrac{1}{2} * \displaystyle\int \dfrac{2}{(x + 1)(x - 1)} dx \\[5ex] = \dfrac{1}{2} * \left[\displaystyle\int \left(\dfrac{1}{x - 1} - \dfrac{1}{x + 1}\right) dx\right] \\[5ex] = \dfrac{1}{2} * \left[\displaystyle\int \dfrac{1}{x - 1}dx - \displaystyle\int \dfrac{1}{x + 1}dx\right] \\[5ex] = \dfrac{1}{2}[\ln|x - 1| - \ln|x + 1|] + C \\[5ex] = \dfrac{1}{2}\ln\dfrac{|x - 1|}{|x + 1|} + C $
(13.)
(14.) WASSCE:FM
(a) Express $\dfrac{x + 6}{(x + 1)^3}$ in partial fractions
(b) Use the answer in (a) to evaluate $\displaystyle\int_1^2 \dfrac{x + 6}{(x + 1)^3}dx$
$ (a.) \\[3ex] \dfrac{x + 6}{(x + 1)^3} \\[5ex] $ Numerator: cannot be simplified further
Denominator: cannot be simplified further
Form: Proper Fraction: Repeated Linear Factors at the Denominator
$ \dfrac{x + 6}{(x + 1)^3} \\[5ex] = \dfrac{A}{x + 1} + \dfrac{B}{(x + 1)^2} + \dfrac{C}{(x + 1)^3} \\[5ex] = \dfrac{A(x + 1)^2 + B(x + 1) + C}{(x + 1)^3} \\[5ex] = \dfrac{A[(x + 1)(x + 1)] + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{A[x^2 + x + x + 1] + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{A[x^2 + 2x + 1] + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{Ax^2 + 2Ax + A + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{Ax^2 + 2Ax + Bx + A + B + C}{(x + 1)^3} \\[5ex] $ Denominators are the same
Equate the numerators
$ x + 6 = Ax^2 + 2Ax + Bx + A + B + C \\[3ex] Swap \\[3ex] Ax^2 + 2Ax + Bx + A + B + C = x + 6 \\[3ex] Ax^2 + x(2A + B) + A + B + C = 0x^2 + x + 6 \\[3ex] \implies \\[3ex] A = 0...eqn.(1) \\[3ex] 2A + B = 1...eqn.(2) \\[3ex] A + B + C = 6...eqn.(3) \\[3ex] Substitute\;\;eqn.(1)\;\;in\;\;eqn.(2) \\[3ex] 2(0) + B = 1 \\[3ex] 0 + B = 1 \\[3ex] B = 1 - 0 \\[3ex] B = 1 \\[3ex] Substitute\;\;0\;\;for\;\;A\;\;and\;\;1\;\;for\;\;B\;\;in\;\;eqn.(3) \\[3ex] 0 + 1 + C = 6 \\[3ex] 1 + C = 6 \\[3ex] C = 6 - 1 \\[3ex] C = 5 \\[3ex] \implies \\[3ex] \dfrac{x + 6}{(x + 1)^3} = \dfrac{0}{x + 1} + \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \dfrac{x + 6}{(x + 1)^3} = 0 + \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \therefore \dfrac{x + 6}{(x + 1)^3} = \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \underline{Check} \\[3ex] \dfrac{x + 6}{(x + 1)^3} = \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \underline{RHS} \\[3ex] \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] = \dfrac{1(x + 1) + 5}{(x + 1)^3} \\[5ex] = \dfrac{x + 1 + 5}{(x + 1)^3} \\[5ex] = \dfrac{x + 6}{(x + 1)^3} \\[5ex] = LHS \\[3ex] $ Integration by Partial Fractions
$ (b.) \\[3ex] \displaystyle\int_1^2 \dfrac{x + 6}{(x + 1)^3} dx \\[5ex] = \displaystyle\int_1^2 \left[\dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3}\right] dx \\[5ex] = \displaystyle\int_1^2 \dfrac{1}{(x + 1)^2} dx + \displaystyle\int_1^2 \dfrac{5}{(x + 1)^3} dx \\[5ex] Let\;\; p = x + 1 \\[3ex] \dfrac{dp}{dx} = 1 \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{1} = 1 \\[5ex] dx = dp \\[3ex] \displaystyle\int \dfrac{1}{(x + 1)^2} dx \\[5ex] = \displaystyle\int \dfrac{1}{p^2} dp \\[5ex] = \displaystyle\int p^{-2} dp \\[5ex] = \dfrac{p^{-2 + 1}}{-2 + 1} \\[5ex] = \dfrac{p^{-1}}{-1} \\[5ex] = -p^{-1} \\[3ex] = -\dfrac{1}{p} \\[5ex] = -\dfrac{1}{x + 1} \\[5ex] \implies \\[3ex] \displaystyle\int_1^2 \dfrac{1}{(x + 1)^2} dx \\[5ex] = \left[-\dfrac{1}{x + 1}\right]_1^2 \\[5ex] = -\dfrac{1}{2 + 1} - -\dfrac{1}{1 + 1} \\[5ex] = -\dfrac{1}{3} + \dfrac{1}{2} \\[5ex] = \dfrac{-2 + 3}{6} \\[5ex] = \dfrac{1}{6} \\[7ex] \displaystyle\int \dfrac{5}{(x + 1)^3} dx \\[5ex] = 5\displaystyle\int \dfrac{1}{(x + 1)^3} dx \\[5ex] = 5\displaystyle\int \dfrac{1}{p^3} dp \\[5ex] = 5\displaystyle\int p^{-3} dp \\[5ex] = 5 * \dfrac{p^{-3 + 1}}{-3 + 1} \\[5ex] = 5 * \dfrac{p^{-2}}{-2} \\[5ex] = -\dfrac{5}{2} * p^{-2} \\[5ex] = -\dfrac{5}{2} * \dfrac{1}{p^2} \\[5ex] = -\dfrac{5}{2p^2} \\[5ex] = -\dfrac{5}{2(x + 1)^2} \\[5ex] \implies \\[3ex] \displaystyle\int_1^2 \dfrac{5}{(x + 1)^3} dx \\[5ex] = \left[-\dfrac{5}{2(x + 1)^2}\right]_1^2 \\[5ex] = -\dfrac{5}{2(2 + 1)^2} - -\dfrac{5}{2(1 + 1)^2} \\[5ex] = -\dfrac{5}{2(3)^2} + \dfrac{5}{2(2)^2} \\[5ex] = -\dfrac{5}{2(9)} + \dfrac{5}{2(4)} \\[5ex] = -\dfrac{5}{18} + \dfrac{5}{8} \\[5ex] = \dfrac{-20 + 45}{72} \\[5ex] = \dfrac{25}{72} \\[7ex] \implies \\[3ex] \displaystyle\int_1^2 \dfrac{1}{(x + 1)^2} dx + \displaystyle\int_1^2 \dfrac{5}{(x + 1)^3} dx \\[5ex] = \dfrac{1}{6} + \dfrac{25}{72} \\[5ex] = \dfrac{12 + 25}{72} \\[5ex] = \dfrac{37}{72} \\[5ex] \therefore \displaystyle\int_1^2 \dfrac{x + 6}{(x + 1)^3} dx = \dfrac{37}{72} $
(a) Express $\dfrac{x + 6}{(x + 1)^3}$ in partial fractions
(b) Use the answer in (a) to evaluate $\displaystyle\int_1^2 \dfrac{x + 6}{(x + 1)^3}dx$
$ (a.) \\[3ex] \dfrac{x + 6}{(x + 1)^3} \\[5ex] $ Numerator: cannot be simplified further
Denominator: cannot be simplified further
Form: Proper Fraction: Repeated Linear Factors at the Denominator
$ \dfrac{x + 6}{(x + 1)^3} \\[5ex] = \dfrac{A}{x + 1} + \dfrac{B}{(x + 1)^2} + \dfrac{C}{(x + 1)^3} \\[5ex] = \dfrac{A(x + 1)^2 + B(x + 1) + C}{(x + 1)^3} \\[5ex] = \dfrac{A[(x + 1)(x + 1)] + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{A[x^2 + x + x + 1] + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{A[x^2 + 2x + 1] + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{Ax^2 + 2Ax + A + Bx + B + C}{(x + 1)^3} \\[5ex] = \dfrac{Ax^2 + 2Ax + Bx + A + B + C}{(x + 1)^3} \\[5ex] $ Denominators are the same
Equate the numerators
$ x + 6 = Ax^2 + 2Ax + Bx + A + B + C \\[3ex] Swap \\[3ex] Ax^2 + 2Ax + Bx + A + B + C = x + 6 \\[3ex] Ax^2 + x(2A + B) + A + B + C = 0x^2 + x + 6 \\[3ex] \implies \\[3ex] A = 0...eqn.(1) \\[3ex] 2A + B = 1...eqn.(2) \\[3ex] A + B + C = 6...eqn.(3) \\[3ex] Substitute\;\;eqn.(1)\;\;in\;\;eqn.(2) \\[3ex] 2(0) + B = 1 \\[3ex] 0 + B = 1 \\[3ex] B = 1 - 0 \\[3ex] B = 1 \\[3ex] Substitute\;\;0\;\;for\;\;A\;\;and\;\;1\;\;for\;\;B\;\;in\;\;eqn.(3) \\[3ex] 0 + 1 + C = 6 \\[3ex] 1 + C = 6 \\[3ex] C = 6 - 1 \\[3ex] C = 5 \\[3ex] \implies \\[3ex] \dfrac{x + 6}{(x + 1)^3} = \dfrac{0}{x + 1} + \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \dfrac{x + 6}{(x + 1)^3} = 0 + \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \therefore \dfrac{x + 6}{(x + 1)^3} = \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \underline{Check} \\[3ex] \dfrac{x + 6}{(x + 1)^3} = \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] \underline{RHS} \\[3ex] \dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3} \\[5ex] = \dfrac{1(x + 1) + 5}{(x + 1)^3} \\[5ex] = \dfrac{x + 1 + 5}{(x + 1)^3} \\[5ex] = \dfrac{x + 6}{(x + 1)^3} \\[5ex] = LHS \\[3ex] $ Integration by Partial Fractions
$ (b.) \\[3ex] \displaystyle\int_1^2 \dfrac{x + 6}{(x + 1)^3} dx \\[5ex] = \displaystyle\int_1^2 \left[\dfrac{1}{(x + 1)^2} + \dfrac{5}{(x + 1)^3}\right] dx \\[5ex] = \displaystyle\int_1^2 \dfrac{1}{(x + 1)^2} dx + \displaystyle\int_1^2 \dfrac{5}{(x + 1)^3} dx \\[5ex] Let\;\; p = x + 1 \\[3ex] \dfrac{dp}{dx} = 1 \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{1} = 1 \\[5ex] dx = dp \\[3ex] \displaystyle\int \dfrac{1}{(x + 1)^2} dx \\[5ex] = \displaystyle\int \dfrac{1}{p^2} dp \\[5ex] = \displaystyle\int p^{-2} dp \\[5ex] = \dfrac{p^{-2 + 1}}{-2 + 1} \\[5ex] = \dfrac{p^{-1}}{-1} \\[5ex] = -p^{-1} \\[3ex] = -\dfrac{1}{p} \\[5ex] = -\dfrac{1}{x + 1} \\[5ex] \implies \\[3ex] \displaystyle\int_1^2 \dfrac{1}{(x + 1)^2} dx \\[5ex] = \left[-\dfrac{1}{x + 1}\right]_1^2 \\[5ex] = -\dfrac{1}{2 + 1} - -\dfrac{1}{1 + 1} \\[5ex] = -\dfrac{1}{3} + \dfrac{1}{2} \\[5ex] = \dfrac{-2 + 3}{6} \\[5ex] = \dfrac{1}{6} \\[7ex] \displaystyle\int \dfrac{5}{(x + 1)^3} dx \\[5ex] = 5\displaystyle\int \dfrac{1}{(x + 1)^3} dx \\[5ex] = 5\displaystyle\int \dfrac{1}{p^3} dp \\[5ex] = 5\displaystyle\int p^{-3} dp \\[5ex] = 5 * \dfrac{p^{-3 + 1}}{-3 + 1} \\[5ex] = 5 * \dfrac{p^{-2}}{-2} \\[5ex] = -\dfrac{5}{2} * p^{-2} \\[5ex] = -\dfrac{5}{2} * \dfrac{1}{p^2} \\[5ex] = -\dfrac{5}{2p^2} \\[5ex] = -\dfrac{5}{2(x + 1)^2} \\[5ex] \implies \\[3ex] \displaystyle\int_1^2 \dfrac{5}{(x + 1)^3} dx \\[5ex] = \left[-\dfrac{5}{2(x + 1)^2}\right]_1^2 \\[5ex] = -\dfrac{5}{2(2 + 1)^2} - -\dfrac{5}{2(1 + 1)^2} \\[5ex] = -\dfrac{5}{2(3)^2} + \dfrac{5}{2(2)^2} \\[5ex] = -\dfrac{5}{2(9)} + \dfrac{5}{2(4)} \\[5ex] = -\dfrac{5}{18} + \dfrac{5}{8} \\[5ex] = \dfrac{-20 + 45}{72} \\[5ex] = \dfrac{25}{72} \\[7ex] \implies \\[3ex] \displaystyle\int_1^2 \dfrac{1}{(x + 1)^2} dx + \displaystyle\int_1^2 \dfrac{5}{(x + 1)^3} dx \\[5ex] = \dfrac{1}{6} + \dfrac{25}{72} \\[5ex] = \dfrac{12 + 25}{72} \\[5ex] = \dfrac{37}{72} \\[5ex] \therefore \displaystyle\int_1^2 \dfrac{x + 6}{(x + 1)^3} dx = \dfrac{37}{72} $
(15.) Cambridge:O-Level (a.) Evaluate $\displaystyle\int_{\dfrac{\pi}{3}}^{\dfrac{\pi}{2}}
\cos \dfrac{x}{4}dx$
You must show all your working.
(b.) Find $\displaystyle\int\left(\dfrac{1}{4x - 3} + \dfrac{1}{x^3}\right) dx$
$ (a.) \\[3ex] \displaystyle\int_{\dfrac{\pi}{3}}^{\dfrac{\pi}{2}} \cos \dfrac{x}{4}dx \\[5ex] ..................................................................... \\[3ex] \displaystyle\int \cos \dfrac{x}{4}dx \\[5ex] = \dfrac{1}{4} \displaystyle\int \cos x dx \\[5ex] = \dfrac{1}{4}\sin x + C \\[5ex] ..................................................................... \\[3ex] \implies \\[3ex] = \dfrac{1}{4}\left(\sin\dfrac{\pi}{2} - \sin\dfrac{\pi}{3}\right) \\[5ex] = \dfrac{1}{4}\left(1 - \dfrac{\sqrt{3}}{2}\right) \\[5ex] = \dfrac{1}{4}\left(\dfrac{2 - \sqrt{3}}{2}\right) \\[5ex] = \dfrac{2 - \sqrt{3}}{8} \\[5ex] (b.) \\[3ex] \displaystyle\int\left(\dfrac{1}{4x - 3} + \dfrac{1}{x^3}\right) dx \\[5ex] = \displaystyle\int\dfrac{1}{4x - 3} dx + \displaystyle\int\dfrac{1}{x^3}dx \\[5ex] ..................................................................... \\[3ex] \text{For } \displaystyle\int\dfrac{1}{4x - 3} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = 4x - 3 \\[3ex] \dfrac{dp}{dx} = 4 \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{4} \\[5ex] dx = \dfrac{dp}{4} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{1}{p} * \dfrac{dp}{4} \\[5ex] = \dfrac{1}{4} \displaystyle\int \dfrac{dp}{p} \\[5ex] = \dfrac{1}{4}\ln p \\[5ex] = \dfrac{1}{4}\ln(4x + 3) \\[5ex] \text{For } \displaystyle\int\dfrac{1}{x^3}dx \\[5ex] = \displaystyle\int x^{-3} dx \\[5ex] = \dfrac{x^{-3 + 1}}{-3 + 1} \\[5ex] = \dfrac{x^{-2}}{-2} \\[5ex] = -\dfrac{1}{2} * \dfrac{1}{x^2} \\[5ex] = -\dfrac{1}{2x^2} \\[5ex] ..................................................................... \\[3ex] \implies \\[3ex] \displaystyle\int\dfrac{1}{4x - 3} dx + \displaystyle\int\dfrac{1}{x^3}dx \\[5ex] = \dfrac{1}{4}\ln(4x + 3) -\dfrac{1}{2x^2} + C $
You must show all your working.
(b.) Find $\displaystyle\int\left(\dfrac{1}{4x - 3} + \dfrac{1}{x^3}\right) dx$
$ (a.) \\[3ex] \displaystyle\int_{\dfrac{\pi}{3}}^{\dfrac{\pi}{2}} \cos \dfrac{x}{4}dx \\[5ex] ..................................................................... \\[3ex] \displaystyle\int \cos \dfrac{x}{4}dx \\[5ex] = \dfrac{1}{4} \displaystyle\int \cos x dx \\[5ex] = \dfrac{1}{4}\sin x + C \\[5ex] ..................................................................... \\[3ex] \implies \\[3ex] = \dfrac{1}{4}\left(\sin\dfrac{\pi}{2} - \sin\dfrac{\pi}{3}\right) \\[5ex] = \dfrac{1}{4}\left(1 - \dfrac{\sqrt{3}}{2}\right) \\[5ex] = \dfrac{1}{4}\left(\dfrac{2 - \sqrt{3}}{2}\right) \\[5ex] = \dfrac{2 - \sqrt{3}}{8} \\[5ex] (b.) \\[3ex] \displaystyle\int\left(\dfrac{1}{4x - 3} + \dfrac{1}{x^3}\right) dx \\[5ex] = \displaystyle\int\dfrac{1}{4x - 3} dx + \displaystyle\int\dfrac{1}{x^3}dx \\[5ex] ..................................................................... \\[3ex] \text{For } \displaystyle\int\dfrac{1}{4x - 3} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = 4x - 3 \\[3ex] \dfrac{dp}{dx} = 4 \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{4} \\[5ex] dx = \dfrac{dp}{4} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{1}{p} * \dfrac{dp}{4} \\[5ex] = \dfrac{1}{4} \displaystyle\int \dfrac{dp}{p} \\[5ex] = \dfrac{1}{4}\ln p \\[5ex] = \dfrac{1}{4}\ln(4x + 3) \\[5ex] \text{For } \displaystyle\int\dfrac{1}{x^3}dx \\[5ex] = \displaystyle\int x^{-3} dx \\[5ex] = \dfrac{x^{-3 + 1}}{-3 + 1} \\[5ex] = \dfrac{x^{-2}}{-2} \\[5ex] = -\dfrac{1}{2} * \dfrac{1}{x^2} \\[5ex] = -\dfrac{1}{2x^2} \\[5ex] ..................................................................... \\[3ex] \implies \\[3ex] \displaystyle\int\dfrac{1}{4x - 3} dx + \displaystyle\int\dfrac{1}{x^3}dx \\[5ex] = \dfrac{1}{4}\ln(4x + 3) -\dfrac{1}{2x^2} + C $
(16.) Integrate:
(a.) $\displaystyle\int x^3 + 3x^2 - 4x + 5 + \dfrac{2}{x} - \dfrac{3}{x^2} dx$
(b.) $\displaystyle\int xe^{3x^2} dx$
(c.) Check your answer for part (b.) using a method independent of the integration.
Make sure your notation clearly tells what you are doing.
C is the integration constant.
$ (a.) \\[3ex] \text{Power Rule, Constant Multiple Rule and Logarithmic Integration Rule} \\[3ex] \displaystyle\int x^3 + 3x^2 - 4x + 5 + \dfrac{2}{x} - \dfrac{3}{x^2} dx \\[5ex] = \displaystyle\int x^3 + 3x^2 - 4x + 5 + 2x^{-1} - 3x^{-2} dx \\[5ex] = \dfrac{x^4}{4} + \dfrac{3x^3}{3} - \dfrac{4x^2}{2} + 5x + 2\ln|x| - \dfrac{3x^{-1}}{-1} \\[5ex] = \dfrac{x^4}{4} + x^3 - 2x^2 + 5x + 2\ln|x| + \dfrac{3}{x} + C \\[5ex] (b.) \\[3ex] \text{Integration by Algebraic Substitution} \\[3ex] \displaystyle\int xe^{3x^2} dx \\[3ex] \text{Let } p = 3x^2 \\[3ex] \dfrac{dp}{dx} = 6x \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{6x} \\[5ex] dx = \dfrac{dp}{6x} \\[5ex] \implies \\[3ex] \displaystyle\int xe^{p} * \dfrac{dp}{6x} \\[5ex] = \dfrac{1}{6} \displaystyle\int e^p dp \\[5ex] = \dfrac{e^p}{6} \\[5ex] = \dfrac{e^{3x^2}}{6} + C \\[5ex] $ (c.) When you integrate a function with respect to x (in other words, when you integrate the integrand), the result is known as the antiderivative (or integral) of the function with respect to x (wrt x).
When you differentiate the antiderivative wrt x, you get back the function.
So, let us differentiate the antiderivative of the function wrt x.
$ \text{Let } F(x) = \dfrac{e^{3x^2}}{6} \\[5ex] F(x) = \dfrac{1}{6} * e^{3x^2} + C \\[5ex] \text{Let } u = \dfrac{1}{6} \hspace{4em} v = e^{3x^2} \\[5ex] ................................................................. \\[3ex] v = e^{3x^2} \\[3ex] \text{Let }k = 3x^2 \hspace{2em}\implies \hspace{2em} v = e^k \\[3ex] \dfrac{dk}{dx} = 6x \hspace{7em} \dfrac{dv}{dk} = e^k \\[5ex] \dfrac{dv}{dx} = \dfrac{dv}{dk} * \dfrac{dk}{dx} ...\text{Function of a Function Rule} \\[5ex] \dfrac{dv}{dx} = e^k * 6x \\[5ex] \dfrac{dv}{dx} = 6xe^{3x^2} \\[5ex] ................................................................. \\[3ex] \dfrac{du}{dx} = 0 \hspace{6em} \dfrac{dv}{dx} = 6xe^{3x^2} \\[5ex] F'(x) = u\dfrac{dv}{dx} + v\dfrac{du}{dx} ...\text{Product Rule} \\[5ex] F'(x) = \dfrac{1}{6} * 6xe^{3x^2} + e^{3x^2} * 0 \\[5ex] f(x) = F'(x) = xe^{3x^2}...\text{This is the integrand in Part (b.)} $
(a.) $\displaystyle\int x^3 + 3x^2 - 4x + 5 + \dfrac{2}{x} - \dfrac{3}{x^2} dx$
(b.) $\displaystyle\int xe^{3x^2} dx$
(c.) Check your answer for part (b.) using a method independent of the integration.
Make sure your notation clearly tells what you are doing.
C is the integration constant.
$ (a.) \\[3ex] \text{Power Rule, Constant Multiple Rule and Logarithmic Integration Rule} \\[3ex] \displaystyle\int x^3 + 3x^2 - 4x + 5 + \dfrac{2}{x} - \dfrac{3}{x^2} dx \\[5ex] = \displaystyle\int x^3 + 3x^2 - 4x + 5 + 2x^{-1} - 3x^{-2} dx \\[5ex] = \dfrac{x^4}{4} + \dfrac{3x^3}{3} - \dfrac{4x^2}{2} + 5x + 2\ln|x| - \dfrac{3x^{-1}}{-1} \\[5ex] = \dfrac{x^4}{4} + x^3 - 2x^2 + 5x + 2\ln|x| + \dfrac{3}{x} + C \\[5ex] (b.) \\[3ex] \text{Integration by Algebraic Substitution} \\[3ex] \displaystyle\int xe^{3x^2} dx \\[3ex] \text{Let } p = 3x^2 \\[3ex] \dfrac{dp}{dx} = 6x \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{6x} \\[5ex] dx = \dfrac{dp}{6x} \\[5ex] \implies \\[3ex] \displaystyle\int xe^{p} * \dfrac{dp}{6x} \\[5ex] = \dfrac{1}{6} \displaystyle\int e^p dp \\[5ex] = \dfrac{e^p}{6} \\[5ex] = \dfrac{e^{3x^2}}{6} + C \\[5ex] $ (c.) When you integrate a function with respect to x (in other words, when you integrate the integrand), the result is known as the antiderivative (or integral) of the function with respect to x (wrt x).
When you differentiate the antiderivative wrt x, you get back the function.
So, let us differentiate the antiderivative of the function wrt x.
$ \text{Let } F(x) = \dfrac{e^{3x^2}}{6} \\[5ex] F(x) = \dfrac{1}{6} * e^{3x^2} + C \\[5ex] \text{Let } u = \dfrac{1}{6} \hspace{4em} v = e^{3x^2} \\[5ex] ................................................................. \\[3ex] v = e^{3x^2} \\[3ex] \text{Let }k = 3x^2 \hspace{2em}\implies \hspace{2em} v = e^k \\[3ex] \dfrac{dk}{dx} = 6x \hspace{7em} \dfrac{dv}{dk} = e^k \\[5ex] \dfrac{dv}{dx} = \dfrac{dv}{dk} * \dfrac{dk}{dx} ...\text{Function of a Function Rule} \\[5ex] \dfrac{dv}{dx} = e^k * 6x \\[5ex] \dfrac{dv}{dx} = 6xe^{3x^2} \\[5ex] ................................................................. \\[3ex] \dfrac{du}{dx} = 0 \hspace{6em} \dfrac{dv}{dx} = 6xe^{3x^2} \\[5ex] F'(x) = u\dfrac{dv}{dx} + v\dfrac{du}{dx} ...\text{Product Rule} \\[5ex] F'(x) = \dfrac{1}{6} * 6xe^{3x^2} + e^{3x^2} * 0 \\[5ex] f(x) = F'(x) = xe^{3x^2}...\text{This is the integrand in Part (b.)} $
(17.) Evaluate $\displaystyle\int \dfrac{1}{\sqrt{9 - x^2}} dx$
Standard Integral: Trigonometric Substitution
$ \displaystyle\int \dfrac{dx}{\sqrt{a^2 - x^2}} = \sin^{-1}\left(\dfrac{x}{a}\right) + C \\[5ex] For:\;\;\displaystyle\int \dfrac{1}{\sqrt{9 - x^2}} dx \\[5ex] Compare:\;\;a^2 - x^2 \;\;to\;\; 9 - x^2 \\[3ex] a^2 = 9 \\[3ex] a = \sqrt{9} \\[3ex] a = 3 \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{1}{\sqrt{9 - x^2}} dx \\[5ex] = \sin^{-1}\left(\dfrac{x}{3}\right) + C $
Standard Integral: Trigonometric Substitution
$ \displaystyle\int \dfrac{dx}{\sqrt{a^2 - x^2}} = \sin^{-1}\left(\dfrac{x}{a}\right) + C \\[5ex] For:\;\;\displaystyle\int \dfrac{1}{\sqrt{9 - x^2}} dx \\[5ex] Compare:\;\;a^2 - x^2 \;\;to\;\; 9 - x^2 \\[3ex] a^2 = 9 \\[3ex] a = \sqrt{9} \\[3ex] a = 3 \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{1}{\sqrt{9 - x^2}} dx \\[5ex] = \sin^{-1}\left(\dfrac{x}{3}\right) + C $
(18.) Integrate $xe^x$ with respect to x
Integration by Parts
$ \displaystyle\int udv = uv - \displaystyle\int vdu \\[3ex] \displaystyle\int xe^x dx \\[3ex] Let\;\;u = x \qquad\qquad\qquad dv = e^x dx \\[3ex] \dfrac{du}{dx} = 1 \qquad\qquad\qquad\quad v = \displaystyle\int e^x dx \\[5ex] du = dx \qquad\qquad\qquad\quad v = e^x \\[3ex] = x(e^x) - \displaystyle\int e^x dx \\[5ex] = xe^x - e^x + C \\[3ex] = e^x(x - 1) + C $
Integration by Parts
$ \displaystyle\int udv = uv - \displaystyle\int vdu \\[3ex] \displaystyle\int xe^x dx \\[3ex] Let\;\;u = x \qquad\qquad\qquad dv = e^x dx \\[3ex] \dfrac{du}{dx} = 1 \qquad\qquad\qquad\quad v = \displaystyle\int e^x dx \\[5ex] du = dx \qquad\qquad\qquad\quad v = e^x \\[3ex] = x(e^x) - \displaystyle\int e^x dx \\[5ex] = xe^x - e^x + C \\[3ex] = e^x(x - 1) + C $
(19.) Determine the indefinite integral $\displaystyle\int \dfrac{2dt}{\sqrt{16 - 36t^2}}$
Standard Integral: Trigonometric Substitution
$ \displaystyle\int \dfrac{dx}{\sqrt{a^2 - x^2}} = \sin^{-1}\left(\dfrac{x}{a}\right) + C \\[5ex] For:\;\;\displaystyle\int \dfrac{2dt}{\sqrt{16 - 36t^2}} \\[5ex] $ (1.) The coefficient of $t^2$ is not unity. We need to make it unity (make it 1)
(2.) We need to simplify the integral to look like the standard integral
$ \displaystyle\int \dfrac{2dt}{\sqrt{16 - 36t^2}} \\[5ex] = \displaystyle\int \dfrac{2dt}{\sqrt{36\left(\dfrac{16}{36} - t^2\right)}} \\[10ex] = \displaystyle\int \dfrac{2dt}{6\sqrt{\dfrac{4}{9} - t^2}} \\[10ex] = \dfrac{2}{6} \displaystyle\int \dfrac{dt}{\sqrt{\dfrac{2^2}{3^2} - t^2}} \\[10ex] = \dfrac{1}{3} \displaystyle\int \dfrac{dt}{\sqrt{\left(\dfrac{2}{3}\right)^2 - t^2}} \\[10ex] Compare:\;\;a^2 - x^2 \;\;to\;\;\left(\dfrac{2}{3}\right)^2 - t^2 \\[5ex] a = \dfrac{2}{3} \\[5ex] x = t \\[3ex] \implies \\[3ex] = \dfrac{1}{3}\sin^{-1}\left(t \div \dfrac{2}{3}\right) + C \\[5ex] = \dfrac{1}{3}\sin^{-1}\left(\dfrac{3t}{2}\right) + C $
Standard Integral: Trigonometric Substitution
$ \displaystyle\int \dfrac{dx}{\sqrt{a^2 - x^2}} = \sin^{-1}\left(\dfrac{x}{a}\right) + C \\[5ex] For:\;\;\displaystyle\int \dfrac{2dt}{\sqrt{16 - 36t^2}} \\[5ex] $ (1.) The coefficient of $t^2$ is not unity. We need to make it unity (make it 1)
(2.) We need to simplify the integral to look like the standard integral
$ \displaystyle\int \dfrac{2dt}{\sqrt{16 - 36t^2}} \\[5ex] = \displaystyle\int \dfrac{2dt}{\sqrt{36\left(\dfrac{16}{36} - t^2\right)}} \\[10ex] = \displaystyle\int \dfrac{2dt}{6\sqrt{\dfrac{4}{9} - t^2}} \\[10ex] = \dfrac{2}{6} \displaystyle\int \dfrac{dt}{\sqrt{\dfrac{2^2}{3^2} - t^2}} \\[10ex] = \dfrac{1}{3} \displaystyle\int \dfrac{dt}{\sqrt{\left(\dfrac{2}{3}\right)^2 - t^2}} \\[10ex] Compare:\;\;a^2 - x^2 \;\;to\;\;\left(\dfrac{2}{3}\right)^2 - t^2 \\[5ex] a = \dfrac{2}{3} \\[5ex] x = t \\[3ex] \implies \\[3ex] = \dfrac{1}{3}\sin^{-1}\left(t \div \dfrac{2}{3}\right) + C \\[5ex] = \dfrac{1}{3}\sin^{-1}\left(\dfrac{3t}{2}\right) + C $
(20.) Evaluate the definite integral:
$ \displaystyle\int_{4}^{2} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[5ex] $
$ \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \text{ is of the form}: \;\; \displaystyle\int_a^b \dfrac{f(x_1)}{f(x_1) + f(x_2)}dx \\[7ex] $ So, we shall solve it by Functional Transformation in Integration
$ \underline{\text{Original Integral}} \\[3ex] Let\;\;I_1 = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] \underline{\text{Tranformed Function}} \\[3ex] Set\;\; x = (4 + 2) - x \\[3ex] x = 6 - x \\[5ex] 9 - x \\[3ex] = 9 - (6 - x) \\[3ex] = 9 - 6 + x \\[3ex] = 3 + x \\[3ex] = x + 3 \\[5ex] x + 3 \\[3ex] = 6 - x + 3 \\[3ex] = 9 - x \\[5ex] \underline{\text{Transformed Integral}} \\[3ex] Let\;\;I_2 = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(x + 3)}}{\sqrt{\ln(x + 3)} + \sqrt{\ln(9 - x)}} dx \\[7ex] I_1 = I_2 = \text{the integral},\; I \\[3ex] I_1 + I_2 = I + I = 2I \\[3ex] 2I \\[3ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx + \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(x + 3)}}{\sqrt{\ln(x + 3)} + \sqrt{\ln(9 - x)}} dx \\[7ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx + \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(x + 3)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] = \displaystyle\int_{2}^{4} 1dx \\[5ex] = [x]_2^4 \\[5ex] = 4 - 2 \\[3ex] = 2 \\[5ex] 2I = 2 \\[3ex] I = 1 \\[3ex] \therefore \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx = 1 $

$ \displaystyle\int_{4}^{2} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[5ex] $
$ \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \text{ is of the form}: \;\; \displaystyle\int_a^b \dfrac{f(x_1)}{f(x_1) + f(x_2)}dx \\[7ex] $ So, we shall solve it by Functional Transformation in Integration
$ \underline{\text{Original Integral}} \\[3ex] Let\;\;I_1 = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] \underline{\text{Tranformed Function}} \\[3ex] Set\;\; x = (4 + 2) - x \\[3ex] x = 6 - x \\[5ex] 9 - x \\[3ex] = 9 - (6 - x) \\[3ex] = 9 - 6 + x \\[3ex] = 3 + x \\[3ex] = x + 3 \\[5ex] x + 3 \\[3ex] = 6 - x + 3 \\[3ex] = 9 - x \\[5ex] \underline{\text{Transformed Integral}} \\[3ex] Let\;\;I_2 = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(x + 3)}}{\sqrt{\ln(x + 3)} + \sqrt{\ln(9 - x)}} dx \\[7ex] I_1 = I_2 = \text{the integral},\; I \\[3ex] I_1 + I_2 = I + I = 2I \\[3ex] 2I \\[3ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx + \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(x + 3)}}{\sqrt{\ln(x + 3)} + \sqrt{\ln(9 - x)}} dx \\[7ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx + \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(x + 3)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] = \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx \\[7ex] = \displaystyle\int_{2}^{4} 1dx \\[5ex] = [x]_2^4 \\[5ex] = 4 - 2 \\[3ex] = 2 \\[5ex] 2I = 2 \\[3ex] I = 1 \\[3ex] \therefore \displaystyle\int_{2}^{4} \dfrac{\sqrt{\ln(9 - x)}}{\sqrt{\ln(9 - x)} + \sqrt{\ln(x + 3)}} dx = 1 $

(21.) HSC Determine the following:
(a) $\displaystyle\int (2x^2 - x^3) dx$
(b) $\displaystyle\int_0^{\dfrac{\pi}{2}} \dfrac{\sin (x)}{3 - \cos(x)} dx$
(c) $\dfrac{d}{dy} \displaystyle\int_{-1}^y 3x^2 \cos(2x) dx$
$ (a) \\[3ex] \displaystyle\int (2x^2 - x^3) dx \\[5ex] \boldsymbol{Power\;\;Rule} \\[3ex] = \dfrac{2x^3}{3} - \dfrac{x^4}{4} + C \\[5ex] (b) \\[3ex] \displaystyle\int_0^{\dfrac{\pi}{2}} \dfrac{\sin (x)}{3 - \cos(x)} dx ...keep\;\;the\;\;limits\;\;of\;\;integration \\[5ex] \displaystyle\int \dfrac{\sin (x)}{3 - \cos(x)} dx \\[5ex] \boldsymbol{Algebraic\;\;Substitution} \\[3ex] Let\;\; p = 3 - \cos x \\[3ex] \dfrac{dp}{dx} = -(-\sin x) = \sin x \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{\sin x} \\[5ex] dx = \dfrac{dp}{\sin x} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{\sin x}{p} * \dfrac{dp}{\sin x} \\[5ex] = \ln p \\[3ex] = \ln(3 - \cos x) \\[3ex] Bring\;\;the\;\;limits\;\;of\;\;integration \\[3ex] = [\ln(3 - \cos x)]_0^{\dfrac{\pi}{2}} \\[5ex] = \ln\left[3 - \cos\dfrac{\pi}{2}\right] - \ln[3 - \cos 0] \\[5ex] = \ln(3 - 0) - \ln(3 - 1) \\[3ex] = \ln 3 - \ln 2 \\[3ex] = \ln\left(\dfrac{3}{2}\right) \\[5ex] (c) \\[3ex] \dfrac{d}{dy} \displaystyle\int_{-1}^y 3x^2 \cos(2x) dx \\[5ex] \boldsymbol{Derivatives\;\;of\;\;Integrals} \\[3ex] \dfrac{d}{dy} \displaystyle\int_{a(y)}^{b(y)} f(x) dx = f[b(y)] * b'(y) - f[a(y)] * a'(y) \\[5ex] Compare:\;\; \implies \\[3ex] a(y) = -1 \\[3ex] b(y) = y \\[3ex] b'(y) = 1 \\[3ex] a'(y) = 0 \\[3ex] f(x) = 3x^2 \cos(2x) \\[3ex] f[b(y)] = f(y) = 3y^2 \cos(2y) \\[3ex] f[a(y)] = f(-1) = 3(-1)^2 \cos(2 * -1) = 3(1)\cos(-2) = 3\cos(-2) \\[3ex] \implies \\[3ex] = [3y^2\cos(2y) * 1] - [3\cos(-2) * 0] \\[3ex] = 3y^2\cos(2y) - 0 \\[3ex] = 3y^2\cos(2y) $
(a) $\displaystyle\int (2x^2 - x^3) dx$
(b) $\displaystyle\int_0^{\dfrac{\pi}{2}} \dfrac{\sin (x)}{3 - \cos(x)} dx$
(c) $\dfrac{d}{dy} \displaystyle\int_{-1}^y 3x^2 \cos(2x) dx$
$ (a) \\[3ex] \displaystyle\int (2x^2 - x^3) dx \\[5ex] \boldsymbol{Power\;\;Rule} \\[3ex] = \dfrac{2x^3}{3} - \dfrac{x^4}{4} + C \\[5ex] (b) \\[3ex] \displaystyle\int_0^{\dfrac{\pi}{2}} \dfrac{\sin (x)}{3 - \cos(x)} dx ...keep\;\;the\;\;limits\;\;of\;\;integration \\[5ex] \displaystyle\int \dfrac{\sin (x)}{3 - \cos(x)} dx \\[5ex] \boldsymbol{Algebraic\;\;Substitution} \\[3ex] Let\;\; p = 3 - \cos x \\[3ex] \dfrac{dp}{dx} = -(-\sin x) = \sin x \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{\sin x} \\[5ex] dx = \dfrac{dp}{\sin x} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{\sin x}{p} * \dfrac{dp}{\sin x} \\[5ex] = \ln p \\[3ex] = \ln(3 - \cos x) \\[3ex] Bring\;\;the\;\;limits\;\;of\;\;integration \\[3ex] = [\ln(3 - \cos x)]_0^{\dfrac{\pi}{2}} \\[5ex] = \ln\left[3 - \cos\dfrac{\pi}{2}\right] - \ln[3 - \cos 0] \\[5ex] = \ln(3 - 0) - \ln(3 - 1) \\[3ex] = \ln 3 - \ln 2 \\[3ex] = \ln\left(\dfrac{3}{2}\right) \\[5ex] (c) \\[3ex] \dfrac{d}{dy} \displaystyle\int_{-1}^y 3x^2 \cos(2x) dx \\[5ex] \boldsymbol{Derivatives\;\;of\;\;Integrals} \\[3ex] \dfrac{d}{dy} \displaystyle\int_{a(y)}^{b(y)} f(x) dx = f[b(y)] * b'(y) - f[a(y)] * a'(y) \\[5ex] Compare:\;\; \implies \\[3ex] a(y) = -1 \\[3ex] b(y) = y \\[3ex] b'(y) = 1 \\[3ex] a'(y) = 0 \\[3ex] f(x) = 3x^2 \cos(2x) \\[3ex] f[b(y)] = f(y) = 3y^2 \cos(2y) \\[3ex] f[a(y)] = f(-1) = 3(-1)^2 \cos(2 * -1) = 3(1)\cos(-2) = 3\cos(-2) \\[3ex] \implies \\[3ex] = [3y^2\cos(2y) * 1] - [3\cos(-2) * 0] \\[3ex] = 3y^2\cos(2y) - 0 \\[3ex] = 3y^2\cos(2y) $
(22.) Using the substitution $x = 3\tan\theta$, evaluate the indefinite integral
$\displaystyle\int \dfrac{46dx}{x^2\sqrt{x^2 + 9}}$
Integration by Trigonometric Substitution
$ x = 3\tan\theta \\[3ex] \dfrac{dx}{d\theta} = 3\sec^2\theta \\[5ex] dx = 3\sec^2\theta d\theta \\[3ex] x^2 = (3\tan\theta)^2 = 3^2\tan^2\theta = 9\tan^2\theta \\[3ex] x^2 + 9 = 9\tan^2\theta + 9 = 9(\tan^2\theta + 1) = 9\sec^2\theta \\[3ex] \sqrt{x^2 + 9} = \sqrt{9\sec^2\theta} = 3\sec\theta \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{46dx}{x^2\sqrt{x^2 + 9}} \\[5ex] = 46 \displaystyle\int \dfrac{3\sec^2\theta d\theta}{9\tan^2\theta(3\sec\theta)} \\[5ex] = \dfrac{46}{9} \displaystyle\int \dfrac{\sec\theta d\theta}{\tan^2\theta} \\[5ex] $ Let's keep $\dfrac{46}{9}$ for now and focus on integrating $\dfrac{\sec\theta}{\tan^2\theta}$ wrt $\theta$
$ \displaystyle\int \dfrac{\sec\theta d\theta}{\tan^2\theta} \\[5ex] = \displaystyle\int (\sec\theta \div \tan^2\theta) d\theta \\[5ex] = \displaystyle\int \left(\dfrac{1}{\cos\theta} \div \dfrac{\sin^2\theta}{\cos^2\theta}\right) d\theta \\[5ex] = \displaystyle\int \left(\dfrac{1}{\cos\theta} * \dfrac{\cos^2\theta}{\sin^2\theta}\right) d\theta \\[5ex] = \displaystyle\int \dfrac{\cos\theta}{\sin^2\theta} d\theta \\[5ex] $ Integration by Algebraic Substitution
$ Let\;\;p = \sin\theta \\[3ex] \dfrac{dp}{d\theta} = \cos\theta \\[5ex] \dfrac{d\theta}{dp} = \dfrac{1}{\cos\theta} \\[5ex] d\theta = \dfrac{dp}{\cos\theta} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{\cos\theta}{\sin^2\theta} d\theta = \displaystyle\int \dfrac{\cos\theta}{p^2} * \dfrac{dp}{\cos\theta} \\[5ex] = \displaystyle\int p^{-2}dp \\[3ex] = \dfrac{p^{-1}}{-1} \\[5ex] = -p^{-1} \\[3ex] = -\dfrac{1}{p} \\[5ex] Substitute\;\;back\;\;for\;\;p \\[3ex] = -\dfrac{1}{\sin\theta} \\[5ex] Find\;\;\sin\theta\;\;in\;\;terms\;\;of\;\;x \\[3ex] Recall: \\[3ex] x = 3\tan\theta \\[3ex] 3\tan\theta = x \\[3ex] \tan\theta = \dfrac{x}{3} \\[5ex] \tan^2\theta = \dfrac{x^2}{3^2} = \dfrac{x^2}{9} \\[5ex] \tan^2\theta + 1 = \dfrac{x^2}{9} + \dfrac{9}{9} = \dfrac{x^2 + 9}{9} \\[5ex] \sec^2\theta = \tan^2\theta + 1 ...Pythagorean\;\;Identity \\[3ex] \sec^2\theta = \dfrac{x^2 + 9}{9} \\[5ex] \cos^2\theta = \dfrac{1}{\sec^2\theta} = \dfrac{9}{x^2 + 9} \\[5ex] \sin^2\theta = 1 - \cos^2\theta ...Pythagorean\;\;Identity \\[3ex] \sin^2\theta = 1 - \dfrac{9}{x^2 + 9} \\[5ex] \sin^2\theta = \dfrac{x^2 + 9}{x^2 + 9} - \dfrac{9}{x^2 + 9} \\[5ex] \sin^2\theta = \dfrac{x^2 + 9 - 9}{x^2 + 9} \\[5ex] \sin\theta = \sqrt{\sin^2\theta} = \sqrt{\dfrac{x^2}{x^2 + 9}} \\[5ex] \sin\theta = \dfrac{x}{\sqrt{x^2 + 9}} \\[5ex] $ Get back $-\dfrac{1}{\sin\theta}$
$ -\dfrac{1}{\sin\theta} \\[5ex] = -1 \div \dfrac{x}{\sqrt{x^2 + 9}} \\[5ex] = -1 * \dfrac{\sqrt{x^2 + 9}}{x} \\[5ex] = -\dfrac{\sqrt{x^2 + 9}}{x} \\[5ex] $ Get back $\dfrac{46}{9}$
$ \dfrac{46}{9} * -\dfrac{\sqrt{x^2 + 9}}{x} \\[5ex] = -\dfrac{46\sqrt{x^2 + 9}}{9x} \\[5ex] \therefore \displaystyle\int \dfrac{46dx}{x^2\sqrt{x^2 + 9}} = -\dfrac{46\sqrt{x^2 + 9}}{9x} + C $
Integration by Trigonometric Substitution
$ x = 3\tan\theta \\[3ex] \dfrac{dx}{d\theta} = 3\sec^2\theta \\[5ex] dx = 3\sec^2\theta d\theta \\[3ex] x^2 = (3\tan\theta)^2 = 3^2\tan^2\theta = 9\tan^2\theta \\[3ex] x^2 + 9 = 9\tan^2\theta + 9 = 9(\tan^2\theta + 1) = 9\sec^2\theta \\[3ex] \sqrt{x^2 + 9} = \sqrt{9\sec^2\theta} = 3\sec\theta \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{46dx}{x^2\sqrt{x^2 + 9}} \\[5ex] = 46 \displaystyle\int \dfrac{3\sec^2\theta d\theta}{9\tan^2\theta(3\sec\theta)} \\[5ex] = \dfrac{46}{9} \displaystyle\int \dfrac{\sec\theta d\theta}{\tan^2\theta} \\[5ex] $ Let's keep $\dfrac{46}{9}$ for now and focus on integrating $\dfrac{\sec\theta}{\tan^2\theta}$ wrt $\theta$
$ \displaystyle\int \dfrac{\sec\theta d\theta}{\tan^2\theta} \\[5ex] = \displaystyle\int (\sec\theta \div \tan^2\theta) d\theta \\[5ex] = \displaystyle\int \left(\dfrac{1}{\cos\theta} \div \dfrac{\sin^2\theta}{\cos^2\theta}\right) d\theta \\[5ex] = \displaystyle\int \left(\dfrac{1}{\cos\theta} * \dfrac{\cos^2\theta}{\sin^2\theta}\right) d\theta \\[5ex] = \displaystyle\int \dfrac{\cos\theta}{\sin^2\theta} d\theta \\[5ex] $ Integration by Algebraic Substitution
$ Let\;\;p = \sin\theta \\[3ex] \dfrac{dp}{d\theta} = \cos\theta \\[5ex] \dfrac{d\theta}{dp} = \dfrac{1}{\cos\theta} \\[5ex] d\theta = \dfrac{dp}{\cos\theta} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{\cos\theta}{\sin^2\theta} d\theta = \displaystyle\int \dfrac{\cos\theta}{p^2} * \dfrac{dp}{\cos\theta} \\[5ex] = \displaystyle\int p^{-2}dp \\[3ex] = \dfrac{p^{-1}}{-1} \\[5ex] = -p^{-1} \\[3ex] = -\dfrac{1}{p} \\[5ex] Substitute\;\;back\;\;for\;\;p \\[3ex] = -\dfrac{1}{\sin\theta} \\[5ex] Find\;\;\sin\theta\;\;in\;\;terms\;\;of\;\;x \\[3ex] Recall: \\[3ex] x = 3\tan\theta \\[3ex] 3\tan\theta = x \\[3ex] \tan\theta = \dfrac{x}{3} \\[5ex] \tan^2\theta = \dfrac{x^2}{3^2} = \dfrac{x^2}{9} \\[5ex] \tan^2\theta + 1 = \dfrac{x^2}{9} + \dfrac{9}{9} = \dfrac{x^2 + 9}{9} \\[5ex] \sec^2\theta = \tan^2\theta + 1 ...Pythagorean\;\;Identity \\[3ex] \sec^2\theta = \dfrac{x^2 + 9}{9} \\[5ex] \cos^2\theta = \dfrac{1}{\sec^2\theta} = \dfrac{9}{x^2 + 9} \\[5ex] \sin^2\theta = 1 - \cos^2\theta ...Pythagorean\;\;Identity \\[3ex] \sin^2\theta = 1 - \dfrac{9}{x^2 + 9} \\[5ex] \sin^2\theta = \dfrac{x^2 + 9}{x^2 + 9} - \dfrac{9}{x^2 + 9} \\[5ex] \sin^2\theta = \dfrac{x^2 + 9 - 9}{x^2 + 9} \\[5ex] \sin\theta = \sqrt{\sin^2\theta} = \sqrt{\dfrac{x^2}{x^2 + 9}} \\[5ex] \sin\theta = \dfrac{x}{\sqrt{x^2 + 9}} \\[5ex] $ Get back $-\dfrac{1}{\sin\theta}$
$ -\dfrac{1}{\sin\theta} \\[5ex] = -1 \div \dfrac{x}{\sqrt{x^2 + 9}} \\[5ex] = -1 * \dfrac{\sqrt{x^2 + 9}}{x} \\[5ex] = -\dfrac{\sqrt{x^2 + 9}}{x} \\[5ex] $ Get back $\dfrac{46}{9}$
$ \dfrac{46}{9} * -\dfrac{\sqrt{x^2 + 9}}{x} \\[5ex] = -\dfrac{46\sqrt{x^2 + 9}}{9x} \\[5ex] \therefore \displaystyle\int \dfrac{46dx}{x^2\sqrt{x^2 + 9}} = -\dfrac{46\sqrt{x^2 + 9}}{9x} + C $
(23.)
(24.)
(25.)
$ (25.1) \\[3ex] Function:\;\;h(x) = ax^3 + bx^2 \\[3ex] For\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] y = h(x) = 32 \\[3ex] \implies \\[3ex] 32 = a(4)^3 + b(4)^2 \\[3ex] 32 = 64a + 16b \\[3ex] 64a + 16b = 32 \\[3ex] \implies \\[3ex] 4a + b = 2 ...eqn.(1) \\[3ex] Also: \\[3ex] h(x) = ax^3 + bx^2 \\[3ex] h'(x) = 3ax^2 + 2bx \\[3ex] At\;\;turning\;\;point,\;\;h'(x) = 0 \\[3ex] For\;\;Turning\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] \implies \\[3ex] h'(4) = 0 \\[3ex] h'(4) = 3a(4)^2 + 2b(4) = 0 \\[3ex] 48a + 8b = 0 \\[3ex] \implies \\[3ex] 6a + b = 0 ...eqn.(2) \\[3ex] eqn.(2) - eqn.(1) \\[3ex] 6a - 4a = 0 - 2 \\[3ex] 2a = -2 \\[3ex] a = -\dfrac{2}{2} \\[5ex] a = -1 \\[3ex] Substitute\;\;a = -1 \;\;into\;\;eqn.(1) \\[3ex] 4(-1) + b = 2 \\[3ex] -4 + b = 2 \\[3ex] b = 2 + 4 \\[3ex] b = 6 \\[3ex] \therefore h(x) = -x^3 + 6x^2 \\[3ex] (25.2) \\[3ex] A = x-intercept\;\;of\;\;h(x) \\[3ex] \implies \\[3ex] h(x) = 0 \\[3ex] -x^3 + 6x^2 = 0 \\[3ex] x^2(-x + 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; -x + 6 = 0 \\[3ex] x = \pm \sqrt{0} \;\;\;OR\;\;\; 6 = 0 + x \\[3ex] x = \pm 0 \;\;\;OR\;\;\; 6 = x \\[3ex] Based\;\;on\;\;the\;\;graph:\;\; x \ne \pm 0 \\[3ex] x = 6 \\[3ex] \therefore coordinates\;\;of\;\;A = (6, 0) \\[3ex] (25.3) \\[3ex] (25.3.1) \\[3ex] Based\;\;on\;\;the\;\;Graph \\[3ex] h(x)\uparrow for\;\; x \in (0, 4) \\[3ex] (25.3.2) \\[3ex] Based\;\;on\;\;the\;\;function \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h'(x) = -3x^2 + 12x \\[3ex] h''(x) = -6x + 12 \\[3ex] h''(x) = 0 \\[3ex] \implies \\[3ex] -6x + 12 = 0 \\[3ex] -6x = -12 \\[3ex] x = \dfrac{-12}{-6} \\[5ex] Inflection\;\;Point:\;\;x = 2 \\[3ex] Intervals:\;\; x \lt 2 \;\;and\;\; x \gt 2 \\[3ex] $
$ h(x)\frown for\;\; x \gt 2 \\[3ex] h(x)\frown for\;\; x \in (2, \infty) \\[3ex] (25.4) \\[3ex] -(x - 1)^3 + 6(x - 1)^2 - k = 0 \\[3ex] -(x - 1)^3 + 6(x - 1)^2 = k \\[3ex] k = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] \implies k = h(x - 1) \\[3ex] k = graph\;\;of\;\;h(x - 1) \\[3ex] 1st\;\;find\;\;the\;\;y-intercept...value\;\;of\;\;k\;\;when\;\;x = 0 \\[3ex] k = -(0 - 1)^3 + 6(0 - 1)^2 \\[3ex] k = -(-1)^3 + 6(-1)^2 \\[3ex] k = -(-1) + 6(1) \\[3ex] k = 1 + 6 \\[3ex] k = 7 \\[3ex] Negative\;\;root \implies x \lt 0 \\[3ex] When\;\;x \lt 0,\;\;k \lt 7 \\[3ex] Let\;\;us\;\;find\;\;the\;\;maximum\;\;value\;\;for\;\;the\;\;positive\;\;roots \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x - 1)' = -3(x - 1)^2 + 12(x - 1) \\[3ex] h(x - 1)' = 0 \\[3ex] \implies \\[3ex] -3(x - 1)^2 + 12(x - 1) = 0 \\[3ex] -3(x^2 - 2x + 1) + 12x - 12 = 0 \\[3ex] -3x^2 + 6x - 3 + 12x - 12 = 0 \\[3ex] -3x^2 + 18x - 15 = 0 \\[3ex] x^2 - 6x + 5 = 0 \\[3ex] (x - 5)(x - 1) = 0 \\[3ex] x - 5 = 0 \;\;\;OR\;\;\; x - 1 = 0 \\[3ex] x = 5 \;\;\;OR\;\;\; x = 1 \\[3ex] For\;\;x = 5 \\[3ex] h(x - 1) = -(5 - 1)^3 + 6(5 - 1)^2 \\[3ex] = -4^3 + 6(4^2) \\[3ex] = -64 + 6(16) \\[3ex] = -64 + 96 \\[3ex] = 32 \\[3ex] For\;\;x = 1 \\[3ex] h(x - 1) = -(1 - 1)^3 + 6(0 - 1)^2 \\[3ex] = -0^3 + 6(-1)^2 \\[3ex] = 0 + 6(1) \\[3ex] = 0 + 6 \\[3ex] = 6 \\[3ex] Maximum\;\;value = 32 \\[3ex] \implies \\[3ex] 7 \lt k \lt 32 $
$ (25.1) \\[3ex] Function:\;\;h(x) = ax^3 + bx^2 \\[3ex] For\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] y = h(x) = 32 \\[3ex] \implies \\[3ex] 32 = a(4)^3 + b(4)^2 \\[3ex] 32 = 64a + 16b \\[3ex] 64a + 16b = 32 \\[3ex] \implies \\[3ex] 4a + b = 2 ...eqn.(1) \\[3ex] Also: \\[3ex] h(x) = ax^3 + bx^2 \\[3ex] h'(x) = 3ax^2 + 2bx \\[3ex] At\;\;turning\;\;point,\;\;h'(x) = 0 \\[3ex] For\;\;Turning\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] \implies \\[3ex] h'(4) = 0 \\[3ex] h'(4) = 3a(4)^2 + 2b(4) = 0 \\[3ex] 48a + 8b = 0 \\[3ex] \implies \\[3ex] 6a + b = 0 ...eqn.(2) \\[3ex] eqn.(2) - eqn.(1) \\[3ex] 6a - 4a = 0 - 2 \\[3ex] 2a = -2 \\[3ex] a = -\dfrac{2}{2} \\[5ex] a = -1 \\[3ex] Substitute\;\;a = -1 \;\;into\;\;eqn.(1) \\[3ex] 4(-1) + b = 2 \\[3ex] -4 + b = 2 \\[3ex] b = 2 + 4 \\[3ex] b = 6 \\[3ex] \therefore h(x) = -x^3 + 6x^2 \\[3ex] (25.2) \\[3ex] A = x-intercept\;\;of\;\;h(x) \\[3ex] \implies \\[3ex] h(x) = 0 \\[3ex] -x^3 + 6x^2 = 0 \\[3ex] x^2(-x + 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; -x + 6 = 0 \\[3ex] x = \pm \sqrt{0} \;\;\;OR\;\;\; 6 = 0 + x \\[3ex] x = \pm 0 \;\;\;OR\;\;\; 6 = x \\[3ex] Based\;\;on\;\;the\;\;graph:\;\; x \ne \pm 0 \\[3ex] x = 6 \\[3ex] \therefore coordinates\;\;of\;\;A = (6, 0) \\[3ex] (25.3) \\[3ex] (25.3.1) \\[3ex] Based\;\;on\;\;the\;\;Graph \\[3ex] h(x)\uparrow for\;\; x \in (0, 4) \\[3ex] (25.3.2) \\[3ex] Based\;\;on\;\;the\;\;function \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h'(x) = -3x^2 + 12x \\[3ex] h''(x) = -6x + 12 \\[3ex] h''(x) = 0 \\[3ex] \implies \\[3ex] -6x + 12 = 0 \\[3ex] -6x = -12 \\[3ex] x = \dfrac{-12}{-6} \\[5ex] Inflection\;\;Point:\;\;x = 2 \\[3ex] Intervals:\;\; x \lt 2 \;\;and\;\; x \gt 2 \\[3ex] $
| Interval | $x \lt 2$ | $x \gt 2$ |
| Test Value | $x = 1$ | $x = 3$ |
| Sign Test | $$ -6(1) + 12 \\[3ex] -6 + 12 = 6 \\[3ex] 6 \gt 0 \\[3ex] positive $$ | $$ -6(3) + 12 \\[3ex] -18 + 12 = -6 \\[3ex] -6 \lt 0 \\[3ex] negative $$ |
| Conclusion | Concave up | Concave down |
$ h(x)\frown for\;\; x \gt 2 \\[3ex] h(x)\frown for\;\; x \in (2, \infty) \\[3ex] (25.4) \\[3ex] -(x - 1)^3 + 6(x - 1)^2 - k = 0 \\[3ex] -(x - 1)^3 + 6(x - 1)^2 = k \\[3ex] k = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] \implies k = h(x - 1) \\[3ex] k = graph\;\;of\;\;h(x - 1) \\[3ex] 1st\;\;find\;\;the\;\;y-intercept...value\;\;of\;\;k\;\;when\;\;x = 0 \\[3ex] k = -(0 - 1)^3 + 6(0 - 1)^2 \\[3ex] k = -(-1)^3 + 6(-1)^2 \\[3ex] k = -(-1) + 6(1) \\[3ex] k = 1 + 6 \\[3ex] k = 7 \\[3ex] Negative\;\;root \implies x \lt 0 \\[3ex] When\;\;x \lt 0,\;\;k \lt 7 \\[3ex] Let\;\;us\;\;find\;\;the\;\;maximum\;\;value\;\;for\;\;the\;\;positive\;\;roots \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x - 1)' = -3(x - 1)^2 + 12(x - 1) \\[3ex] h(x - 1)' = 0 \\[3ex] \implies \\[3ex] -3(x - 1)^2 + 12(x - 1) = 0 \\[3ex] -3(x^2 - 2x + 1) + 12x - 12 = 0 \\[3ex] -3x^2 + 6x - 3 + 12x - 12 = 0 \\[3ex] -3x^2 + 18x - 15 = 0 \\[3ex] x^2 - 6x + 5 = 0 \\[3ex] (x - 5)(x - 1) = 0 \\[3ex] x - 5 = 0 \;\;\;OR\;\;\; x - 1 = 0 \\[3ex] x = 5 \;\;\;OR\;\;\; x = 1 \\[3ex] For\;\;x = 5 \\[3ex] h(x - 1) = -(5 - 1)^3 + 6(5 - 1)^2 \\[3ex] = -4^3 + 6(4^2) \\[3ex] = -64 + 6(16) \\[3ex] = -64 + 96 \\[3ex] = 32 \\[3ex] For\;\;x = 1 \\[3ex] h(x - 1) = -(1 - 1)^3 + 6(0 - 1)^2 \\[3ex] = -0^3 + 6(-1)^2 \\[3ex] = 0 + 6(1) \\[3ex] = 0 + 6 \\[3ex] = 6 \\[3ex] Maximum\;\;value = 32 \\[3ex] \implies \\[3ex] 7 \lt k \lt 32 $
(26.)
(27.)
(28.)
(29.)
$ (a.) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = 7x^{-1} - 7\ln x \\[3ex] f'(x) = -7x^-2 - \left[7\left(\dfrac{1}{x}\right) + \ln x(0)\right] \\[5ex] f'(x) = -7x^{-2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] Simplify\;\;f(x)\;\;and\;\;f'(x) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = \dfrac{7 - 7x\ln x}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7 - 7x}{x^2} \\[5ex] \dfrac{f(x)}{f'(x)} \\[5ex] = f(x) \div f'(x) \\[3ex] = \dfrac{7 - 7x\ln x}{x} \div \dfrac{-7 - 7x}{x^2} \\[5ex] = \dfrac{7 - 7x\ln x}{x} * \dfrac{x^2}{-7 - 7x} \\[5ex] = \dfrac{7(1 - x\ln x)}{x} * \dfrac{x^2}{-7(1 + x)} \\[5ex] = \dfrac{x(1 - x\ln x)}{-(1 + x)} \\[5ex] = \dfrac{x - x^2\ln x}{-(1 + x)} \\[5ex] = -\dfrac{(x - x^2\ln x)}{1 + x} \\[5ex] = \dfrac{-x + x^2\ln x}{x + 1} \\[5ex] = \dfrac{x^2\ln x - x}{x + 1} \\[5ex] x - \dfrac{f(x)}{f'(x)} \\[5ex] = x - \dfrac{x^2\ln x - x}{x + 1} \\[5ex] = \dfrac{x(x + 1) - (x^2\ln x - x)}{x + 1} \\[5ex] = \dfrac{x^2 + x - x^2\ln x + x}{x + 1} \\[5ex] = \dfrac{x^2 + 2x - x^2\ln x}{x + 1} \\[5ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = \dfrac{x_n^2 + 2x_n - x_n^2\ln x_n}{x_n + 1} \\[5ex] x_1 = 1 \\[3ex] \implies \\[3ex] x_2 = \dfrac{x_1^2 + 2x_1 - x_1^2\ln x_1}{x_1 + 1} \\[5ex] x_2 = \dfrac{1^2 + 2(1) - 1^2 * \ln(1)}{1 + 1} \\[5ex] x_2 = \dfrac{1 + 2 - 1 * 0}{2} \\[5ex] x_2 = \dfrac{1 + 2 - 0}{2} \\[5ex] x_2 = \dfrac{3}{2} \\[7ex] x_3 = \dfrac{x_2^2 + 2x_2 - x_2^2\ln x_2}{x_2 + 1} \\[5ex] \underline{Numerator} \\[3ex] x_2^2 + 2x_2 - x_2^2\ln x_2 \\[3ex] = \left(\dfrac{3}{2}\right)^2 + 2 * \dfrac{3}{2} - \left(\dfrac{3}{2}\right)^2 * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{9}{4} + 3 - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] \underline{Denominator} \\[3ex] x_2 + 1 \\[3ex] = \dfrac{3}{2} + 1 \\[5ex] = \dfrac{3 + 2}{2} \\[5ex] = \dfrac{5}{2} \\[5ex] Numerator \div Denominator \\[3ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \div \dfrac{5}{2} \\[5ex] = \dfrac{1}{4}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] * \dfrac{2}{5} \\[5ex] = \dfrac{1}{10}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] \\[5ex] = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] \therefore x_3 = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] (b.) \\[3ex] x_3 = 2.1 - (0.9 * \ln(1.5)) \\[3ex] x_3 = 1.735081403 \\[3ex] $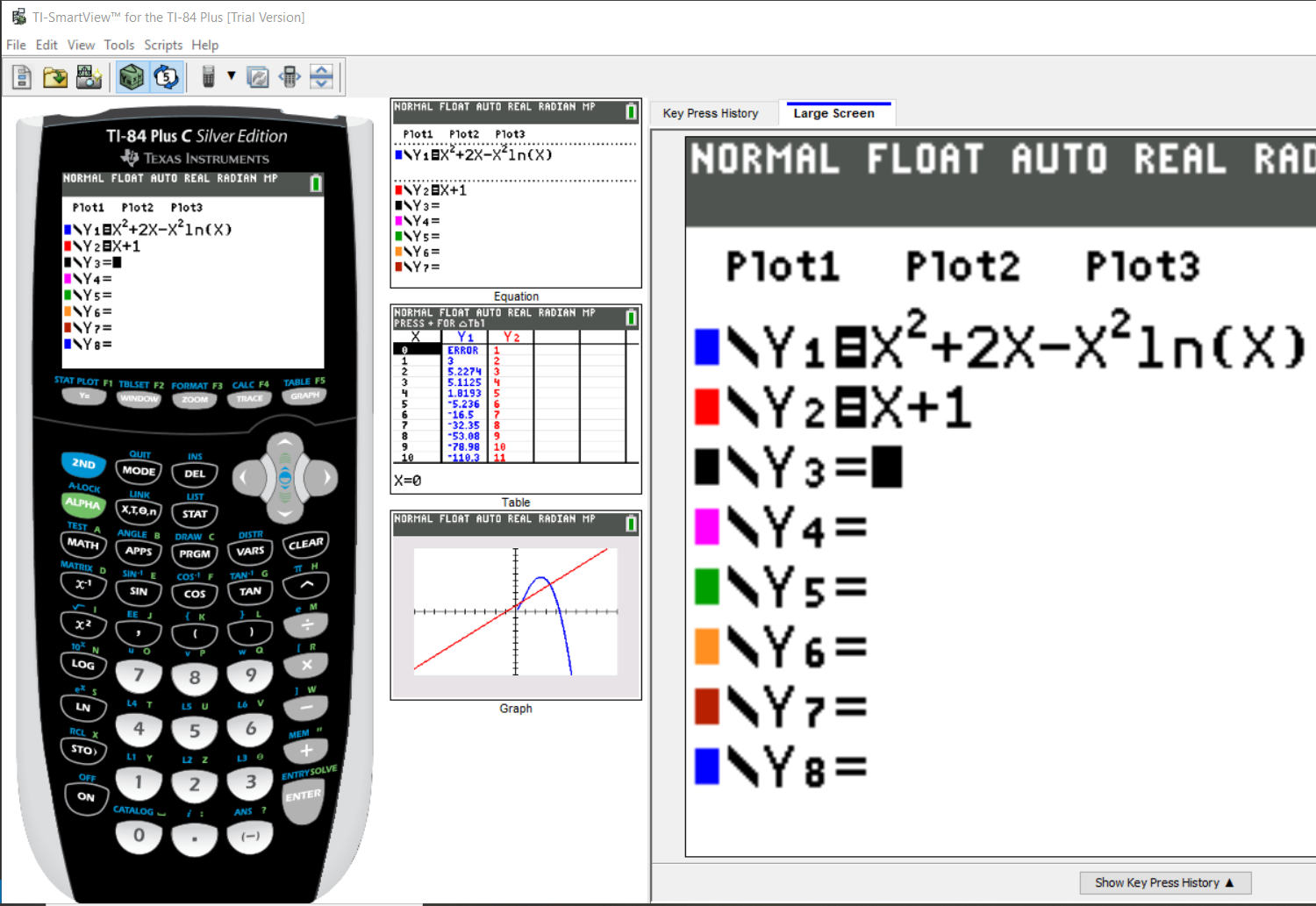
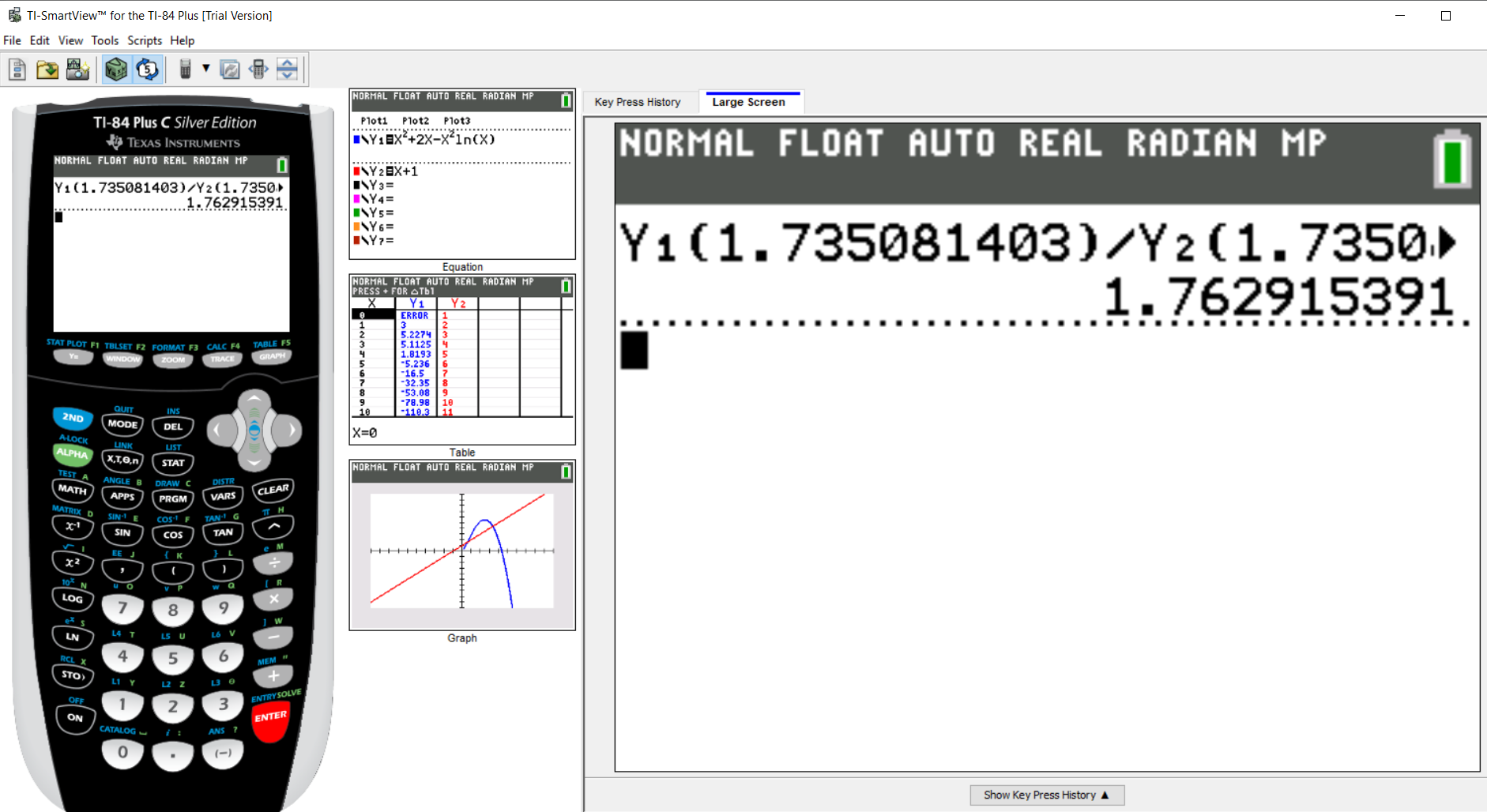
$ x_4 = 1.762915391 \\[3ex] $
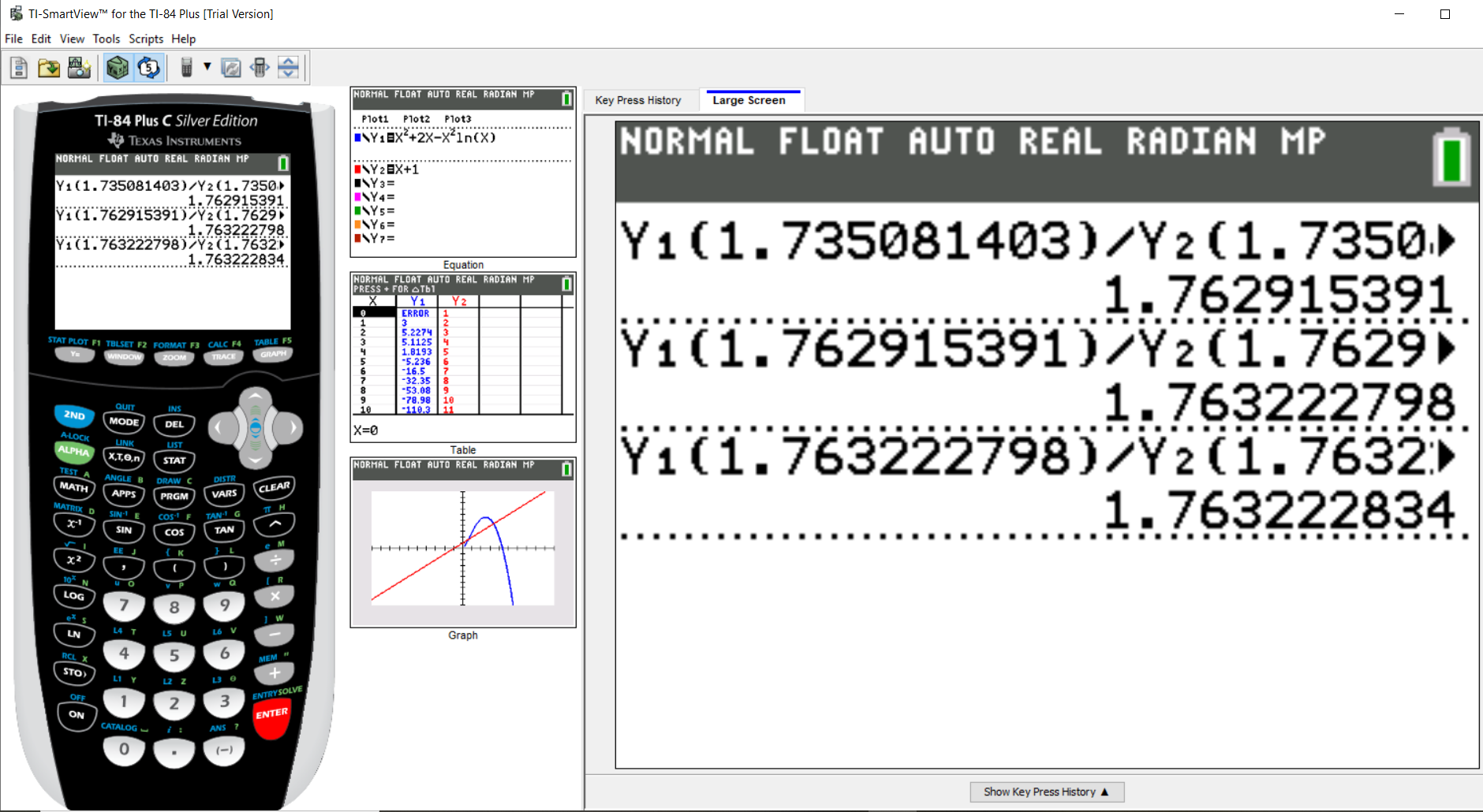
$ x_5 = 1.763222798 \\[3ex] x_6 = 1.763222834 \\[3ex] Because\;\;x_5 \approx x_6...STOP $
$ (a.) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = 7x^{-1} - 7\ln x \\[3ex] f'(x) = -7x^-2 - \left[7\left(\dfrac{1}{x}\right) + \ln x(0)\right] \\[5ex] f'(x) = -7x^{-2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] Simplify\;\;f(x)\;\;and\;\;f'(x) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = \dfrac{7 - 7x\ln x}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7 - 7x}{x^2} \\[5ex] \dfrac{f(x)}{f'(x)} \\[5ex] = f(x) \div f'(x) \\[3ex] = \dfrac{7 - 7x\ln x}{x} \div \dfrac{-7 - 7x}{x^2} \\[5ex] = \dfrac{7 - 7x\ln x}{x} * \dfrac{x^2}{-7 - 7x} \\[5ex] = \dfrac{7(1 - x\ln x)}{x} * \dfrac{x^2}{-7(1 + x)} \\[5ex] = \dfrac{x(1 - x\ln x)}{-(1 + x)} \\[5ex] = \dfrac{x - x^2\ln x}{-(1 + x)} \\[5ex] = -\dfrac{(x - x^2\ln x)}{1 + x} \\[5ex] = \dfrac{-x + x^2\ln x}{x + 1} \\[5ex] = \dfrac{x^2\ln x - x}{x + 1} \\[5ex] x - \dfrac{f(x)}{f'(x)} \\[5ex] = x - \dfrac{x^2\ln x - x}{x + 1} \\[5ex] = \dfrac{x(x + 1) - (x^2\ln x - x)}{x + 1} \\[5ex] = \dfrac{x^2 + x - x^2\ln x + x}{x + 1} \\[5ex] = \dfrac{x^2 + 2x - x^2\ln x}{x + 1} \\[5ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = \dfrac{x_n^2 + 2x_n - x_n^2\ln x_n}{x_n + 1} \\[5ex] x_1 = 1 \\[3ex] \implies \\[3ex] x_2 = \dfrac{x_1^2 + 2x_1 - x_1^2\ln x_1}{x_1 + 1} \\[5ex] x_2 = \dfrac{1^2 + 2(1) - 1^2 * \ln(1)}{1 + 1} \\[5ex] x_2 = \dfrac{1 + 2 - 1 * 0}{2} \\[5ex] x_2 = \dfrac{1 + 2 - 0}{2} \\[5ex] x_2 = \dfrac{3}{2} \\[7ex] x_3 = \dfrac{x_2^2 + 2x_2 - x_2^2\ln x_2}{x_2 + 1} \\[5ex] \underline{Numerator} \\[3ex] x_2^2 + 2x_2 - x_2^2\ln x_2 \\[3ex] = \left(\dfrac{3}{2}\right)^2 + 2 * \dfrac{3}{2} - \left(\dfrac{3}{2}\right)^2 * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{9}{4} + 3 - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] \underline{Denominator} \\[3ex] x_2 + 1 \\[3ex] = \dfrac{3}{2} + 1 \\[5ex] = \dfrac{3 + 2}{2} \\[5ex] = \dfrac{5}{2} \\[5ex] Numerator \div Denominator \\[3ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \div \dfrac{5}{2} \\[5ex] = \dfrac{1}{4}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] * \dfrac{2}{5} \\[5ex] = \dfrac{1}{10}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] \\[5ex] = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] \therefore x_3 = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] (b.) \\[3ex] x_3 = 2.1 - (0.9 * \ln(1.5)) \\[3ex] x_3 = 1.735081403 \\[3ex] $


$ x_4 = 1.762915391 \\[3ex] $

$ x_5 = 1.763222798 \\[3ex] x_6 = 1.763222834 \\[3ex] Because\;\;x_5 \approx x_6...STOP $
(30.) If $x f(x) = 3[f(x)]^2 + 2$, then $\displaystyle\int \dfrac{2x^2 - 12\cdot f(x) + f(x)}{[6f(x)
- x][x^2 -
f(x)]^2} dx$ is equal to
$ (A.)\;\; \dfrac{1}{x^2 - f(x)} + C \\[5ex] (B.)\;\; \dfrac{1}{x^2 + xf(x)} + C \\[5ex] (C.)\;\; \dfrac{1}{[x - f(x)]^2} + C \\[5ex] (D.)\;\; \dfrac{1}{[6f(x) - x]^2} + C \\[5ex] $
This is not a straightforward integration problem
So, we need to see what we can do to simplify the integrand
Let us begin with the function we were given
Let us differentiate that function.
$ x f(x) = 3[f(x)]^2 + 2 \\[3ex] \text{Differentiating the function implicitly, we have} \\[3ex] xf'(x) + f(x)(1) = 3[f(x)f'(x) + f(x)f'(x)] + [f(x)]^2(0) + 0 \\[3ex] xf'(x) + f(x) = 3[2f(x)f'(x)] \\[3ex] xf'(x) + f(x) = 6f(x)f'(x) \\[3ex] f(x) = 6f(x)f'(x) - xf'(x) \\[3ex] f(x) = f'(x)[6f(x) - x] ...eqn.(1) \\[3ex] $ We notice that this modified function is one of the denominators of the integrand.
So, we see some ray of hope in simplifying the integrand
Let us dive back to the numerator of the integrand
$ \underline{\text{Numerator of the integrand}} \\[3ex] 2x^2 - 12\cdot f(x) + f(x) \\[3ex] 2x[x - 6f(x)] + f(x) \\[3ex] \text{Rewrite the first term; Substitute for the 2nd term from eqn.(1)} \\[3ex] -2x[-x + 6f(x)] + f'(x)[6f(x) - x] \\[3ex] -2x[6f(x) - x] + f'(x)[6f(x) - x] \\[3ex] [6f(x) - x][-2x + f'(x)] \\[3ex] [6f(x) - x][f'(x) - 2x] \\[3ex] $ Okay, something can cancel out from the numerator and the denominator of the integrand
Let's continue
$ \displaystyle\int \dfrac{2x^2 - 12\cdot f(x) + f(x)}{[6f(x) - x][x^2 - f(x)]^2} dx \\[5ex] = \displaystyle\int \dfrac{[6f(x) - x][f'(x) - 2x]}{[6f(x) - x][x^2 - f(x)]^2} dx \\[5ex] = \displaystyle\int \dfrac{f'(x) - 2x}{[x^2 - f(x)]^2} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = x^2 - f(x) \\[3ex] \dfrac{dp}{dx} = 2x - f'(x) \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{2x - f'(x)} \\[5ex] dx = \dfrac{dp}{2x - f'(x)} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{f'(x) - 2x}{p^2} * \dfrac{dp}{2x - f'(x)} \\[5ex] = \displaystyle\int \dfrac{-[f'(x) - 2x] * dp}{-p^2 * [2x - f'(x)]} \\[5ex] = \displaystyle\int \dfrac{[2x - f'(x)] * dp}{-p^2 * [2x - f'(x)]} \\[5ex] = -\displaystyle\int \dfrac{dp}{p^2} \\[5ex] = -\displaystyle\int p^{-2} dp \\[3ex] = \dfrac{-p^{-1}}{-1} + C \\[5ex] = \dfrac{1}{p} + C \\[5ex] = \dfrac{1}{x^2 - f(x)} + C...\text{Option (A.)} $
$ (A.)\;\; \dfrac{1}{x^2 - f(x)} + C \\[5ex] (B.)\;\; \dfrac{1}{x^2 + xf(x)} + C \\[5ex] (C.)\;\; \dfrac{1}{[x - f(x)]^2} + C \\[5ex] (D.)\;\; \dfrac{1}{[6f(x) - x]^2} + C \\[5ex] $
This is not a straightforward integration problem
So, we need to see what we can do to simplify the integrand
Let us begin with the function we were given
Let us differentiate that function.
$ x f(x) = 3[f(x)]^2 + 2 \\[3ex] \text{Differentiating the function implicitly, we have} \\[3ex] xf'(x) + f(x)(1) = 3[f(x)f'(x) + f(x)f'(x)] + [f(x)]^2(0) + 0 \\[3ex] xf'(x) + f(x) = 3[2f(x)f'(x)] \\[3ex] xf'(x) + f(x) = 6f(x)f'(x) \\[3ex] f(x) = 6f(x)f'(x) - xf'(x) \\[3ex] f(x) = f'(x)[6f(x) - x] ...eqn.(1) \\[3ex] $ We notice that this modified function is one of the denominators of the integrand.
So, we see some ray of hope in simplifying the integrand
Let us dive back to the numerator of the integrand
$ \underline{\text{Numerator of the integrand}} \\[3ex] 2x^2 - 12\cdot f(x) + f(x) \\[3ex] 2x[x - 6f(x)] + f(x) \\[3ex] \text{Rewrite the first term; Substitute for the 2nd term from eqn.(1)} \\[3ex] -2x[-x + 6f(x)] + f'(x)[6f(x) - x] \\[3ex] -2x[6f(x) - x] + f'(x)[6f(x) - x] \\[3ex] [6f(x) - x][-2x + f'(x)] \\[3ex] [6f(x) - x][f'(x) - 2x] \\[3ex] $ Okay, something can cancel out from the numerator and the denominator of the integrand
Let's continue
$ \displaystyle\int \dfrac{2x^2 - 12\cdot f(x) + f(x)}{[6f(x) - x][x^2 - f(x)]^2} dx \\[5ex] = \displaystyle\int \dfrac{[6f(x) - x][f'(x) - 2x]}{[6f(x) - x][x^2 - f(x)]^2} dx \\[5ex] = \displaystyle\int \dfrac{f'(x) - 2x}{[x^2 - f(x)]^2} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } p = x^2 - f(x) \\[3ex] \dfrac{dp}{dx} = 2x - f'(x) \\[5ex] \dfrac{dx}{dp} = \dfrac{1}{2x - f'(x)} \\[5ex] dx = \dfrac{dp}{2x - f'(x)} \\[5ex] \implies \\[3ex] \displaystyle\int \dfrac{f'(x) - 2x}{p^2} * \dfrac{dp}{2x - f'(x)} \\[5ex] = \displaystyle\int \dfrac{-[f'(x) - 2x] * dp}{-p^2 * [2x - f'(x)]} \\[5ex] = \displaystyle\int \dfrac{[2x - f'(x)] * dp}{-p^2 * [2x - f'(x)]} \\[5ex] = -\displaystyle\int \dfrac{dp}{p^2} \\[5ex] = -\displaystyle\int p^{-2} dp \\[3ex] = \dfrac{-p^{-1}}{-1} + C \\[5ex] = \dfrac{1}{p} + C \\[5ex] = \dfrac{1}{x^2 - f(x)} + C...\text{Option (A.)} $
(31.)
(32.)
(33.)
(34.)
(35.) Show that $\displaystyle\int_{-1}^0 3\ln(2x + 3) dx = \dfrac{3}{2}(\ln 27 - 2)$
Show all work.
$ \underline{\text{From the LHS}} \\[3ex] \displaystyle\int_{-1}^0 3\ln(2x + 3) dx \\[3ex] \underline{\text{Integration by Parts}} \\[3ex] \displaystyle\int udv = uv - \displaystyle\int vdu \\[3ex] \text{Let } u = \ln(2x + 3) \hspace{4em} dv = 3dx \\[3ex] ................................................................ \\[3ex] u = \ln(2x + 3) \\[3ex] \underline{\text{Differentiation by Chain Rule}} \\[3ex] \text{Let }p = 3x + 3 \hspace{4em} u = \ln p \\[3ex] \dfrac{dp}{dx} = 2 \hspace{6em} \dfrac{du}{dp} = \dfrac{1}{p} \\[5ex] \dfrac{du}{dx} = \dfrac{du}{dp} * \dfrac{dp}{dx} ...\text{Chain Rule} \\[5ex] = 2 * \dfrac{1}{p} \\[5ex] = \dfrac{2}{p} \\[5ex] = \dfrac{2}{2x + 3} \\[5ex] ................................................................ \\[3ex] dv = 3dx \\[3ex] \displaystyle\int dv = \displaystyle\int 3dx \\[3ex] v = 3x \\[3ex] ................................................................ \\[3ex] \implies \\[3ex] \displaystyle\int 3\ln(2x + 3) dx \\[3ex] = 3x\ln(2x + 3) - \displaystyle\int 3x * \dfrac{2}{2x + 3} \\[5ex] = 3x\ln(2x + 3) - \displaystyle\int \dfrac{6x}{2x + 3} dx \\[5ex] ................................................................ \\[3ex] \displaystyle\int \dfrac{6x}{2x + 3} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } k = 2x + 3 \\[3ex] 2x = k - 3 \\[3ex] x = \dfrac{k - 3}{2} \\[5ex] Also: \\[3ex] \dfrac{dk}{dx} = 2 \\[5ex] dx = \dfrac{dk}{2} \\[5ex] ................................................................ \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{6x}{2x + 3} \\[5ex] = \displaystyle\int 6x * \dfrac{1}{2x + 3} dx \\[5ex] = \displaystyle\int 6\left(\dfrac{k - 3}{2}\right) * \dfrac{1}{k} * \dfrac{dk}{2} \\[5ex] = \displaystyle\int \dfrac{3(k - 3)}{2k} dk \\[5ex] = \displaystyle\int \left(\dfrac{3k - 9}{2k}\right) dk \\[5ex] = \displaystyle\int \dfrac{3k}{2k} dk - \displaystyle\int \dfrac{9}{2k} dk \\[5ex] = \dfrac{3}{2}\displaystyle\int dk - \dfrac{9}{2}\ln k \\[5ex] = \dfrac{3k}{2} - \dfrac{9\ln(2x + 3)}{2} \\[5ex] = \dfrac{3(2x + 3)}{2} - \dfrac{9\ln(2x + 3)}{2} \\[5ex] = \dfrac{6x}{2} + \dfrac{9}{2} - \dfrac{9\ln(2x + 3)}{2} \\[5ex] = 3x - \dfrac{9\ln(2x + 3)}{2} \\[5ex] \implies \\[3ex] \displaystyle\int 3\ln(2x + 3) dx \\[3ex] = 3x\ln(2x + 3) - \left[3x + \dfrac{9}{2} - \dfrac{9\ln(2x + 3)}{2}\right] + C \\[5ex] = 3x\ln(2x + 3) - 3x - \dfrac{9}{2} + \dfrac{9\ln(2x + 3)}{2} + C \\[5ex] = 3x\ln(2x + 3) - 3x + \dfrac{9\ln(2x + 3)}{2} - \dfrac{9}{2} + C \\[5ex] = 3x\ln(2x + 3) - 3x + \dfrac{9\ln(2x + 3)}{2} + C \\[5ex] \implies \\[3ex] \displaystyle\int_{-1}^0 3\ln(2x + 3) dx \\[3ex] = \left[3x\ln(2x + 3) - 3x + \dfrac{9\ln(2x + 3)}{2}\right]_{-1}^0 \\[5ex] = \left[3(0)\ln[2(0) + 3] - 3(0) + \dfrac{9\ln[2(0) + 3]}{2}\right] - \left[3(-1)\ln[2(-1) + 3] - 3(-1) + \dfrac{9\ln[2(-1) + 3]}{2}\right] \\[5ex] = \left(0 - 0 + \dfrac{9\ln 3}{2}\right) - \left[-3\ln 1 + 3 + \dfrac{9\ln 1}{2}\right] \\[5ex] = \dfrac{9\ln 3}{2} - \left[-3(0) + 3 + \dfrac{9(0)}{2}\right] \\[5ex] = \dfrac{9\ln 3}{2} - (0 + 3 + 0) \\[5ex] = \dfrac{9\ln 3}{2} - 3 \\[5ex] = \dfrac{3}{2}(3\ln 3 - 2) \\[5ex] = \dfrac{3}{2}(\ln 3^3 - 2) \\[5ex] = \dfrac{3}{2}(\ln 27 - 2) \\[5ex] = RHS $
Show all work.
$ \underline{\text{From the LHS}} \\[3ex] \displaystyle\int_{-1}^0 3\ln(2x + 3) dx \\[3ex] \underline{\text{Integration by Parts}} \\[3ex] \displaystyle\int udv = uv - \displaystyle\int vdu \\[3ex] \text{Let } u = \ln(2x + 3) \hspace{4em} dv = 3dx \\[3ex] ................................................................ \\[3ex] u = \ln(2x + 3) \\[3ex] \underline{\text{Differentiation by Chain Rule}} \\[3ex] \text{Let }p = 3x + 3 \hspace{4em} u = \ln p \\[3ex] \dfrac{dp}{dx} = 2 \hspace{6em} \dfrac{du}{dp} = \dfrac{1}{p} \\[5ex] \dfrac{du}{dx} = \dfrac{du}{dp} * \dfrac{dp}{dx} ...\text{Chain Rule} \\[5ex] = 2 * \dfrac{1}{p} \\[5ex] = \dfrac{2}{p} \\[5ex] = \dfrac{2}{2x + 3} \\[5ex] ................................................................ \\[3ex] dv = 3dx \\[3ex] \displaystyle\int dv = \displaystyle\int 3dx \\[3ex] v = 3x \\[3ex] ................................................................ \\[3ex] \implies \\[3ex] \displaystyle\int 3\ln(2x + 3) dx \\[3ex] = 3x\ln(2x + 3) - \displaystyle\int 3x * \dfrac{2}{2x + 3} \\[5ex] = 3x\ln(2x + 3) - \displaystyle\int \dfrac{6x}{2x + 3} dx \\[5ex] ................................................................ \\[3ex] \displaystyle\int \dfrac{6x}{2x + 3} dx \\[5ex] \underline{\text{Integration by Algebraic Substitution}} \\[3ex] \text{Let } k = 2x + 3 \\[3ex] 2x = k - 3 \\[3ex] x = \dfrac{k - 3}{2} \\[5ex] Also: \\[3ex] \dfrac{dk}{dx} = 2 \\[5ex] dx = \dfrac{dk}{2} \\[5ex] ................................................................ \\[3ex] \implies \\[3ex] \displaystyle\int \dfrac{6x}{2x + 3} \\[5ex] = \displaystyle\int 6x * \dfrac{1}{2x + 3} dx \\[5ex] = \displaystyle\int 6\left(\dfrac{k - 3}{2}\right) * \dfrac{1}{k} * \dfrac{dk}{2} \\[5ex] = \displaystyle\int \dfrac{3(k - 3)}{2k} dk \\[5ex] = \displaystyle\int \left(\dfrac{3k - 9}{2k}\right) dk \\[5ex] = \displaystyle\int \dfrac{3k}{2k} dk - \displaystyle\int \dfrac{9}{2k} dk \\[5ex] = \dfrac{3}{2}\displaystyle\int dk - \dfrac{9}{2}\ln k \\[5ex] = \dfrac{3k}{2} - \dfrac{9\ln(2x + 3)}{2} \\[5ex] = \dfrac{3(2x + 3)}{2} - \dfrac{9\ln(2x + 3)}{2} \\[5ex] = \dfrac{6x}{2} + \dfrac{9}{2} - \dfrac{9\ln(2x + 3)}{2} \\[5ex] = 3x - \dfrac{9\ln(2x + 3)}{2} \\[5ex] \implies \\[3ex] \displaystyle\int 3\ln(2x + 3) dx \\[3ex] = 3x\ln(2x + 3) - \left[3x + \dfrac{9}{2} - \dfrac{9\ln(2x + 3)}{2}\right] + C \\[5ex] = 3x\ln(2x + 3) - 3x - \dfrac{9}{2} + \dfrac{9\ln(2x + 3)}{2} + C \\[5ex] = 3x\ln(2x + 3) - 3x + \dfrac{9\ln(2x + 3)}{2} - \dfrac{9}{2} + C \\[5ex] = 3x\ln(2x + 3) - 3x + \dfrac{9\ln(2x + 3)}{2} + C \\[5ex] \implies \\[3ex] \displaystyle\int_{-1}^0 3\ln(2x + 3) dx \\[3ex] = \left[3x\ln(2x + 3) - 3x + \dfrac{9\ln(2x + 3)}{2}\right]_{-1}^0 \\[5ex] = \left[3(0)\ln[2(0) + 3] - 3(0) + \dfrac{9\ln[2(0) + 3]}{2}\right] - \left[3(-1)\ln[2(-1) + 3] - 3(-1) + \dfrac{9\ln[2(-1) + 3]}{2}\right] \\[5ex] = \left(0 - 0 + \dfrac{9\ln 3}{2}\right) - \left[-3\ln 1 + 3 + \dfrac{9\ln 1}{2}\right] \\[5ex] = \dfrac{9\ln 3}{2} - \left[-3(0) + 3 + \dfrac{9(0)}{2}\right] \\[5ex] = \dfrac{9\ln 3}{2} - (0 + 3 + 0) \\[5ex] = \dfrac{9\ln 3}{2} - 3 \\[5ex] = \dfrac{3}{2}(3\ln 3 - 2) \\[5ex] = \dfrac{3}{2}(\ln 3^3 - 2) \\[5ex] = \dfrac{3}{2}(\ln 27 - 2) \\[5ex] = RHS $
(36.)
(37.)
(38.)
(39.)
(40.)