Solved Examples: Applications of Integrals
(1.)
There are at least two appraches that we can use to solve the question: Derivatives and Vertex Formula
Derivatives: First Derivative Test
The maximum value is the $y-value$
The derivative is used to find the maximum value.
This is our first approach.
First, find the derivative.
Second, set it to zero and solve for $x$.
Third, substitute the value of $x$ in the function in order to find the $y$
Vertex Formula
The function is a quadratic function.
So, we can find the vertex of the parabola.
This is our second approach.
Use whichever approach you prefer: that you feel is fast and accurate.
$ \underline{\text{First Approach: Derivatives: First Derivative Test}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] \dfrac{dy}{dx} = -2 - 6x \\[5ex] Set\:\:\dfrac{dy}{dx} = 0 \\[5ex] -2 - 6x = 0 \\[3ex] -2 = 6x \\[3ex] 6x = -2 \\[3ex] x = -\dfrac{2}{6} \\[5ex] x = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} \\[5ex] \underline{\text{Second Approach: Vertex Formula}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] y = -3x^2 - 2x + 1 \\[3ex] y = ax^2 + bx + c \\[3ex] \text{Compare} \\[3ex] a = -3 \\[3ex] b = -2 \\[3ex] Vertex = \left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right) \\[5ex] x = -\dfrac{b}{2a} = \dfrac{-(-2)}{2(-3)} = \dfrac{2}{-6} = -\dfrac{2}{6} = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} $
There are at least two appraches that we can use to solve the question: Derivatives and Vertex Formula
Derivatives: First Derivative Test
The maximum value is the $y-value$
The derivative is used to find the maximum value.
This is our first approach.
First, find the derivative.
Second, set it to zero and solve for $x$.
Third, substitute the value of $x$ in the function in order to find the $y$
Vertex Formula
The function is a quadratic function.
So, we can find the vertex of the parabola.
This is our second approach.
Use whichever approach you prefer: that you feel is fast and accurate.
$ \underline{\text{First Approach: Derivatives: First Derivative Test}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] \dfrac{dy}{dx} = -2 - 6x \\[5ex] Set\:\:\dfrac{dy}{dx} = 0 \\[5ex] -2 - 6x = 0 \\[3ex] -2 = 6x \\[3ex] 6x = -2 \\[3ex] x = -\dfrac{2}{6} \\[5ex] x = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} \\[5ex] \underline{\text{Second Approach: Vertex Formula}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] y = -3x^2 - 2x + 1 \\[3ex] y = ax^2 + bx + c \\[3ex] \text{Compare} \\[3ex] a = -3 \\[3ex] b = -2 \\[3ex] Vertex = \left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right) \\[5ex] x = -\dfrac{b}{2a} = \dfrac{-(-2)}{2(-3)} = \dfrac{2}{-6} = -\dfrac{2}{6} = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} $
(2.)
The gradient(slope) of the tangent line is the derivative
$ y = 2kx^2 + x + 1 \:\:at\:\:x = 1 \\[3ex] \dfrac{dy}{dx} = 4kx + 1 \\[5ex] At\:\: x = 1, \:\:\dfrac{dy}{dx} = 9 \\[5ex] \dfrac{dy}{dx}\Big|_{x = 1} = 4 * k * 1 + 1 = 9 \\[5ex] 4k + 1 = 9 \\[3ex] 4k = 9 - 1 \\[3ex] 4k = 8 \\[3ex] k = \dfrac{8}{4} \\[5ex] k = 2 $
The gradient(slope) of the tangent line is the derivative
$ y = 2kx^2 + x + 1 \:\:at\:\:x = 1 \\[3ex] \dfrac{dy}{dx} = 4kx + 1 \\[5ex] At\:\: x = 1, \:\:\dfrac{dy}{dx} = 9 \\[5ex] \dfrac{dy}{dx}\Big|_{x = 1} = 4 * k * 1 + 1 = 9 \\[5ex] 4k + 1 = 9 \\[3ex] 4k = 9 - 1 \\[3ex] 4k = 8 \\[3ex] k = \dfrac{8}{4} \\[5ex] k = 2 $
(3.)
The slope is the derivative
Power Rule
$ y = 2x^2 + 5x - 3 \\[3ex] y' = 4x + 5 \\[3ex] (1, 4) \rightarrow x = 1, y = 4 \\[3ex] y' = 4(1) + 5 \\[3ex] y' = 4 + 5 \\[3ex] y' = 9 $
The slope is the derivative
Power Rule
$ y = 2x^2 + 5x - 3 \\[3ex] y' = 4x + 5 \\[3ex] (1, 4) \rightarrow x = 1, y = 4 \\[3ex] y' = 4(1) + 5 \\[3ex] y' = 4 + 5 \\[3ex] y' = 9 $
(4.)
$ y = 3x^2 - x + 1 \\[3ex] y' = 6x - 1 \\[3ex] \text{gradient} = y'\;\;@\;\;x = -1 \\[3ex] = 6(-1) - 1 \\[3ex] = -6 - 1 \\[3ex] = -7 $
$ y = 3x^2 - x + 1 \\[3ex] y' = 6x - 1 \\[3ex] \text{gradient} = y'\;\;@\;\;x = -1 \\[3ex] = 6(-1) - 1 \\[3ex] = -6 - 1 \\[3ex] = -7 $
(5.)
1st: We shall find the slope of the tangent to the curve at at x = 2.
This is the derivative of the function at x = 2.
2nd: We shall determine the slope of the normal to the curve
The normal to the curve is perpendicular to the tangent to the curve
Hence, the product of the two slopes (product of the slope of the tangent and the slope of the normal) is −1
3rd: We shall determine the point (x1, y1) on the curve
We already know the x-coordinate, but we shall find the y-coordinate
4th: We shall use the Point-Slope Form to determine the equation of the normal to the curve.
$ y = 7x - 5x^2 \\[3ex] \underline{\text{Slope of the tangent to the curve}}, m_T \\[3ex] \dfrac{dy}{dx} = 7 - 10x \\[3ex] @\;x = 2 \\[3ex] m_T = \left.\dfrac{dy}{dx}\right|_{x = 2} \\[5ex] = 7 - 10(2) \\[3ex] = 7 - 20 \\[3ex] = -13 \\[5ex] \underline{\text{Slope of the normal to the curve}}, m_N \\[3ex] m_N * m_T = -1 \\[3ex] m_N * 13 = -1 \\[3ex] m_N = \dfrac{-1}{-13} \\[5ex] m_N = \dfrac{1}{13} \\[5ex] \underline{\text{Point on the curve}}, (x_1, y_1) \\[3ex] y = 7x - 5x^2 \\[3ex] @\;x = 2 \\[3ex] y = 7(2) - 5(2)^2 \\[3ex] = 14 - 5(4) \\[3ex] = 14 - 20 \\[3ex] = -6 \\[3ex] (x_1, y_1) = (2, -6) \\[5ex] \underline{\text{Equation of the normal to the curve}} \\[3ex] \text{Point – Slope Form} \\[3ex] y - y_1 = m_N(x - x_1) \\[4ex] y - -6 = \dfrac{1}{13}(x - 2) \\[5ex] y + 6 = \dfrac{1}{13}x - \dfrac{2}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - 6 \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - \dfrac{78}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{80}{13} \\[5ex] LCD = 13 \\[3ex] \text{Multiply each term by 13} \\[3ex] 13y = 13\left(\dfrac{1}{13}x\right) - 13\left(\dfrac{80}{13}\right) \\[5ex] 13y = x - 80 \\[3ex] 13y - x + 80 = 0 $
1st: We shall find the slope of the tangent to the curve at at x = 2.
This is the derivative of the function at x = 2.
2nd: We shall determine the slope of the normal to the curve
The normal to the curve is perpendicular to the tangent to the curve
Hence, the product of the two slopes (product of the slope of the tangent and the slope of the normal) is −1
3rd: We shall determine the point (x1, y1) on the curve
We already know the x-coordinate, but we shall find the y-coordinate
4th: We shall use the Point-Slope Form to determine the equation of the normal to the curve.
$ y = 7x - 5x^2 \\[3ex] \underline{\text{Slope of the tangent to the curve}}, m_T \\[3ex] \dfrac{dy}{dx} = 7 - 10x \\[3ex] @\;x = 2 \\[3ex] m_T = \left.\dfrac{dy}{dx}\right|_{x = 2} \\[5ex] = 7 - 10(2) \\[3ex] = 7 - 20 \\[3ex] = -13 \\[5ex] \underline{\text{Slope of the normal to the curve}}, m_N \\[3ex] m_N * m_T = -1 \\[3ex] m_N * 13 = -1 \\[3ex] m_N = \dfrac{-1}{-13} \\[5ex] m_N = \dfrac{1}{13} \\[5ex] \underline{\text{Point on the curve}}, (x_1, y_1) \\[3ex] y = 7x - 5x^2 \\[3ex] @\;x = 2 \\[3ex] y = 7(2) - 5(2)^2 \\[3ex] = 14 - 5(4) \\[3ex] = 14 - 20 \\[3ex] = -6 \\[3ex] (x_1, y_1) = (2, -6) \\[5ex] \underline{\text{Equation of the normal to the curve}} \\[3ex] \text{Point – Slope Form} \\[3ex] y - y_1 = m_N(x - x_1) \\[4ex] y - -6 = \dfrac{1}{13}(x - 2) \\[5ex] y + 6 = \dfrac{1}{13}x - \dfrac{2}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - 6 \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - \dfrac{78}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{80}{13} \\[5ex] LCD = 13 \\[3ex] \text{Multiply each term by 13} \\[3ex] 13y = 13\left(\dfrac{1}{13}x\right) - 13\left(\dfrac{80}{13}\right) \\[5ex] 13y = x - 80 \\[3ex] 13y - x + 80 = 0 $
(6.)
$ f(\theta) = \dfrac{4}{6 + 2\cos\theta} \\[5ex] u = 4 \\[3ex] \dfrac{du}{d\theta} = 0 \\[5ex] v = 6 + 2\cos\theta \\[3ex] \dfrac{dv}{d\theta} = 2 * -\sin\theta + \cos\theta * 0 = -2\sin\theta + 0 = -2\sin\theta \\[5ex] f'(\theta) = \dfrac{v\dfrac{du}{d\theta} - u\dfrac{du}{d\theta}}{v^2} \\[5ex] f'(\theta) = \dfrac{(6 + 2\cos\theta)(0) - 4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] f'(\theta) = \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] Set\:\:f'(\theta) = 0 \\[3ex] \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} = 0 \\[5ex] -4(-2\sin\theta) = 0((6 + 2\cos\theta)^2) \\[3ex] 8\sin\theta = 0 \\[3ex] \sin\theta = \dfrac{0}{8} \\[5ex] \sin\theta = 0 \\[3ex] \theta = 0, \pi, 2\pi ...Unit\:\:Circle\:\:Trigonometry \\[3ex] But\:\:\dfrac{\pi}{2} \lt \theta \lt 2\pi...Question \\[3ex] \therefore \theta = \pi = 180^\circ \\[3ex] Substitute\:\:for\:\:\theta\:\:in\:\:the\:\:main\:\:equation \\[3ex] f(\theta) = \dfrac{4}{6 + 2\cos180^\circ} \\[5ex] \cos180^\circ = -1 \\[3ex] f(\theta) = \dfrac{4}{6 + 2(-1)} \\[5ex] f(\theta) = \dfrac{4}{6 - 2} \\[5ex] f(\theta) = \dfrac{4}{4} \\[5ex] f(\theta) = 1 $
$ f(\theta) = \dfrac{4}{6 + 2\cos\theta} \\[5ex] u = 4 \\[3ex] \dfrac{du}{d\theta} = 0 \\[5ex] v = 6 + 2\cos\theta \\[3ex] \dfrac{dv}{d\theta} = 2 * -\sin\theta + \cos\theta * 0 = -2\sin\theta + 0 = -2\sin\theta \\[5ex] f'(\theta) = \dfrac{v\dfrac{du}{d\theta} - u\dfrac{du}{d\theta}}{v^2} \\[5ex] f'(\theta) = \dfrac{(6 + 2\cos\theta)(0) - 4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] f'(\theta) = \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] Set\:\:f'(\theta) = 0 \\[3ex] \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} = 0 \\[5ex] -4(-2\sin\theta) = 0((6 + 2\cos\theta)^2) \\[3ex] 8\sin\theta = 0 \\[3ex] \sin\theta = \dfrac{0}{8} \\[5ex] \sin\theta = 0 \\[3ex] \theta = 0, \pi, 2\pi ...Unit\:\:Circle\:\:Trigonometry \\[3ex] But\:\:\dfrac{\pi}{2} \lt \theta \lt 2\pi...Question \\[3ex] \therefore \theta = \pi = 180^\circ \\[3ex] Substitute\:\:for\:\:\theta\:\:in\:\:the\:\:main\:\:equation \\[3ex] f(\theta) = \dfrac{4}{6 + 2\cos180^\circ} \\[5ex] \cos180^\circ = -1 \\[3ex] f(\theta) = \dfrac{4}{6 + 2(-1)} \\[5ex] f(\theta) = \dfrac{4}{6 - 2} \\[5ex] f(\theta) = \dfrac{4}{4} \\[5ex] f(\theta) = 1 $
(7.)
(8.)
(9.)
(10.)
$ (a.) \\[3ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] = 8x + \dfrac{27}{2} * \dfrac{1}{x^2} \\[5ex] = 8x^1 + \dfrac{27}{2} * x^{-2} \\[5ex] \dfrac{dy}{dx} = 1 * 8x^{1 - 1} + -2 * \dfrac{27}{2} * x^{-2 - 1} \\[5ex] = 8x^0 + -27x^{-3} \\[3ex] = 8(1) - \dfrac{27}{x^3} \\[5ex] = 8 - \dfrac{27}{x^3} \\[5ex] (b.) \\[3ex] \dfrac{dy}{dx} = 0 \\[5ex] 8 - \dfrac{27}{x^3} = 0 \\[5ex] 8 = \dfrac{27}{x^3} \\[5ex] 8x^3 = 27 \\[3ex] x^3 = \dfrac{27}{8} \\[5ex] x = \sqrt[3]{\dfrac{27}{8}} \\[5ex] x = \dfrac{3}{2} \\[5ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] y = 8x + 27 \div 2x^2 \\[5ex] @\; x = \dfrac{3}{2} \\[5ex] y = 8\left(\dfrac{3}{2}\right) + 27 \div 2\left(\dfrac{3}{2}\right)^2 \\[5ex] = 4(3) + 27 \div \dfrac{3^2}{2} \\[5ex] = 12 + 27 \div \dfrac{9}{2} \\[5ex] = 12 + 27 * \dfrac{2}{9} \\[5ex] = 12 + 6 \\[3ex] = 18 \\[3ex] \text{Stationary Point} = (x, y) = \left(\dfrac{3}{2}, 18\right) \\[5ex] $ To determine the nature of the stationary point, let us use the Second Derivative Test
If the second derivative is positive at the stationary point, the graph of the function is concave upward, and the point is a local minimum.
If the second derivative is negative, the graph of the function is concave downward, and the point is a local maximum.
$ \underline{\text{Nature of the Stationary Point: 2nd Derivative Test}} \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] \dfrac{dy}{dx} = 8 - 27x^{-3} \\[5ex] \dfrac{d^2y}{dx^2} = -3 * -27 * x^{-3 - 1} \\[5ex] = 81 * x^{-4} \\[3ex] = \dfrac{81}{x^4} \\[5ex] = 81 \div x^4 \\[3ex] @\; x = \dfrac{3}{2} \\[5ex] \dfrac{d^2y}{dx^2} = 81 \div \left(\dfrac{3}{2}\right)^4 \\[5ex] = 81 \div \dfrac{3^4}{2^4} \\[5ex] = 81 \div \dfrac{81}{16} \\[5ex] = 81 * \dfrac{16}{81} \\[5ex] = 16 \\[3ex] 16 \gt 0 \\[3ex] \therefore \left(\dfrac{3}{2}, 18\right) \text{is a minimum point} \\[5ex] $ Let:
m1 = slope of the tangent to the curve = derivative
m2 = slope of the normal to the curve
The product of the two slopes is −1 because the normal to the curve is perpendicular to the tangent to the curve
$ (c.) \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] @\; (2, 2) \\[3ex] m_1 = \left.\dfrac{dy}{dx}\right|_{x = 2} = 8 - \dfrac{27}{2^3} \\[5ex] = 8 - \dfrac{27}{8} \\[5ex] = \dfrac{64}{8} - \dfrac{27}{8} \\[5ex] = \dfrac{64 - 27}{8} \\[5ex] = \dfrac{37}{8} \\[5ex] m_1 * m_2 = -1 \\[3ex] m_2 = -\dfrac{1}{m_1} \\[5ex] = -1 \div m_1 \\[3ex] = -1 \div \dfrac{37}{8} \\[5ex] = -1 * \dfrac{8}{37} \\[5ex] = -\dfrac{8}{27} \\[5ex] For\;\;(2, 2) \\[3ex] (x_1, y_1) = (2, 2) \\[3ex] x_1 = 2 \\[3ex] y_1 = 2 \\[5ex] \underline{\text{Point — Slope Form}} \\[3ex] y - y_1 = m_2(x - x_1) \\[3ex] y - 2 = -\dfrac{8}{27}(x - 2) \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + 2 \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + \dfrac{74}{37} \\[5ex] y = \dfrac{-8x}{37} + \dfrac{90}{37} \\[5ex] LCD = 37 \\[3ex] 37y = 37\left(\dfrac{-8x}{37}\right) + 37\left(\dfrac{90}{37}\right) \\[5ex] 37y = -8x + 90 \\[3ex] 37y + 8x - 90 = 0 $
$ (a.) \\[3ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] = 8x + \dfrac{27}{2} * \dfrac{1}{x^2} \\[5ex] = 8x^1 + \dfrac{27}{2} * x^{-2} \\[5ex] \dfrac{dy}{dx} = 1 * 8x^{1 - 1} + -2 * \dfrac{27}{2} * x^{-2 - 1} \\[5ex] = 8x^0 + -27x^{-3} \\[3ex] = 8(1) - \dfrac{27}{x^3} \\[5ex] = 8 - \dfrac{27}{x^3} \\[5ex] (b.) \\[3ex] \dfrac{dy}{dx} = 0 \\[5ex] 8 - \dfrac{27}{x^3} = 0 \\[5ex] 8 = \dfrac{27}{x^3} \\[5ex] 8x^3 = 27 \\[3ex] x^3 = \dfrac{27}{8} \\[5ex] x = \sqrt[3]{\dfrac{27}{8}} \\[5ex] x = \dfrac{3}{2} \\[5ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] y = 8x + 27 \div 2x^2 \\[5ex] @\; x = \dfrac{3}{2} \\[5ex] y = 8\left(\dfrac{3}{2}\right) + 27 \div 2\left(\dfrac{3}{2}\right)^2 \\[5ex] = 4(3) + 27 \div \dfrac{3^2}{2} \\[5ex] = 12 + 27 \div \dfrac{9}{2} \\[5ex] = 12 + 27 * \dfrac{2}{9} \\[5ex] = 12 + 6 \\[3ex] = 18 \\[3ex] \text{Stationary Point} = (x, y) = \left(\dfrac{3}{2}, 18\right) \\[5ex] $ To determine the nature of the stationary point, let us use the Second Derivative Test
If the second derivative is positive at the stationary point, the graph of the function is concave upward, and the point is a local minimum.
If the second derivative is negative, the graph of the function is concave downward, and the point is a local maximum.
$ \underline{\text{Nature of the Stationary Point: 2nd Derivative Test}} \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] \dfrac{dy}{dx} = 8 - 27x^{-3} \\[5ex] \dfrac{d^2y}{dx^2} = -3 * -27 * x^{-3 - 1} \\[5ex] = 81 * x^{-4} \\[3ex] = \dfrac{81}{x^4} \\[5ex] = 81 \div x^4 \\[3ex] @\; x = \dfrac{3}{2} \\[5ex] \dfrac{d^2y}{dx^2} = 81 \div \left(\dfrac{3}{2}\right)^4 \\[5ex] = 81 \div \dfrac{3^4}{2^4} \\[5ex] = 81 \div \dfrac{81}{16} \\[5ex] = 81 * \dfrac{16}{81} \\[5ex] = 16 \\[3ex] 16 \gt 0 \\[3ex] \therefore \left(\dfrac{3}{2}, 18\right) \text{is a minimum point} \\[5ex] $ Let:
m1 = slope of the tangent to the curve = derivative
m2 = slope of the normal to the curve
The product of the two slopes is −1 because the normal to the curve is perpendicular to the tangent to the curve
$ (c.) \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] @\; (2, 2) \\[3ex] m_1 = \left.\dfrac{dy}{dx}\right|_{x = 2} = 8 - \dfrac{27}{2^3} \\[5ex] = 8 - \dfrac{27}{8} \\[5ex] = \dfrac{64}{8} - \dfrac{27}{8} \\[5ex] = \dfrac{64 - 27}{8} \\[5ex] = \dfrac{37}{8} \\[5ex] m_1 * m_2 = -1 \\[3ex] m_2 = -\dfrac{1}{m_1} \\[5ex] = -1 \div m_1 \\[3ex] = -1 \div \dfrac{37}{8} \\[5ex] = -1 * \dfrac{8}{37} \\[5ex] = -\dfrac{8}{27} \\[5ex] For\;\;(2, 2) \\[3ex] (x_1, y_1) = (2, 2) \\[3ex] x_1 = 2 \\[3ex] y_1 = 2 \\[5ex] \underline{\text{Point — Slope Form}} \\[3ex] y - y_1 = m_2(x - x_1) \\[3ex] y - 2 = -\dfrac{8}{27}(x - 2) \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + 2 \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + \dfrac{74}{37} \\[5ex] y = \dfrac{-8x}{37} + \dfrac{90}{37} \\[5ex] LCD = 37 \\[3ex] 37y = 37\left(\dfrac{-8x}{37}\right) + 37\left(\dfrac{90}{37}\right) \\[5ex] 37y = -8x + 90 \\[3ex] 37y + 8x - 90 = 0 $
(11.)
(12.)
(13.) WASSCE:FM Find the area enclosed by the curves $y = x^2 - 3x + 2$ and $y = -x^2 + 3x +
2$
$ Points\;\;of\;\;intersection\;\;of\;\;the\;\;two\;\;curves \\[3ex] y = y \\[3ex] \implies \\[3ex] x^2 - 3x + 2 = -x^2 + 3x + 2 \\[3ex] x^2 + x^2 - 3x - 3x + 2 - 2 = 0 \\[3ex] 2x^2 - 6x = 0 \\[3ex] 2x(x - 3) = 0 \\[3ex] 2x = 0 \;\;\;OR\;\;\; x - 3 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 3 \\[3ex] \therefore limits\;\;of\;\;integration\;\;are:\;\; x = 0 \;\;\;AND\;\;\; x = 3 \\[3ex] first\;\;function:\;\; y = x^2 - 3x + 2 \\[3ex] second\;\;function:\;\; y = -x^2 + 3x + 2 \\[3ex] first\;\;function - second\;\;function \\[3ex] = x^2 - 3x + 2 - (-x^2 + 3x + 2) \\[3ex] = x^2 - 3x + 2 + x^2 - 3x - 2 \\[3ex] = 2x^2 - 6x \\[3ex] Area = \displaystyle\int_{lower\;\;limit}^{upper\;\;limit} (first\;\;function - second\;\;function) dx \\[5ex] = \displaystyle\int_{0}^{3} (2x^2 - 6x) dx \\[5ex] = \left[\dfrac{2x^3}{3} - \dfrac{6x^2}{2}\right]_0^3 \\[5ex] = \left[\dfrac{2x^3}{3} - 3x^2\right]_0^3 \\[5ex] x = 3 \\[3ex] \dfrac{2(3)^3}{3} - 3(3)^2 \\[5ex] 18 - 27 \\[3ex] -9 \\[3ex] x = 0 \\[3ex] \dfrac{2(0)^3}{3} - 3(0)^2 \\[5ex] 0 - 0 \\[3ex] 0 \\[3ex] \implies \\[3ex] Area = -9 - 0 \\[3ex] Area = -9 \\[3ex] But:\;\;Area\;\;cannot\;\;be\;\;negative \\[3ex] \therefore Area = 9\;square\;\;units $
$ Points\;\;of\;\;intersection\;\;of\;\;the\;\;two\;\;curves \\[3ex] y = y \\[3ex] \implies \\[3ex] x^2 - 3x + 2 = -x^2 + 3x + 2 \\[3ex] x^2 + x^2 - 3x - 3x + 2 - 2 = 0 \\[3ex] 2x^2 - 6x = 0 \\[3ex] 2x(x - 3) = 0 \\[3ex] 2x = 0 \;\;\;OR\;\;\; x - 3 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 3 \\[3ex] \therefore limits\;\;of\;\;integration\;\;are:\;\; x = 0 \;\;\;AND\;\;\; x = 3 \\[3ex] first\;\;function:\;\; y = x^2 - 3x + 2 \\[3ex] second\;\;function:\;\; y = -x^2 + 3x + 2 \\[3ex] first\;\;function - second\;\;function \\[3ex] = x^2 - 3x + 2 - (-x^2 + 3x + 2) \\[3ex] = x^2 - 3x + 2 + x^2 - 3x - 2 \\[3ex] = 2x^2 - 6x \\[3ex] Area = \displaystyle\int_{lower\;\;limit}^{upper\;\;limit} (first\;\;function - second\;\;function) dx \\[5ex] = \displaystyle\int_{0}^{3} (2x^2 - 6x) dx \\[5ex] = \left[\dfrac{2x^3}{3} - \dfrac{6x^2}{2}\right]_0^3 \\[5ex] = \left[\dfrac{2x^3}{3} - 3x^2\right]_0^3 \\[5ex] x = 3 \\[3ex] \dfrac{2(3)^3}{3} - 3(3)^2 \\[5ex] 18 - 27 \\[3ex] -9 \\[3ex] x = 0 \\[3ex] \dfrac{2(0)^3}{3} - 3(0)^2 \\[5ex] 0 - 0 \\[3ex] 0 \\[3ex] \implies \\[3ex] Area = -9 - 0 \\[3ex] Area = -9 \\[3ex] But:\;\;Area\;\;cannot\;\;be\;\;negative \\[3ex] \therefore Area = 9\;square\;\;units $
(14.) NSC Determine the following integrals:
$ (14.1) \;\;\; \displaystyle\int x(x^2 + 6x)dx \\[3ex] (14.2) \;\;\; \displaystyle\int \left(3^x + \dfrac{1}{x}\right)dx \\[5ex] $ (14.3) The sketch below represents the area bounded by the function g defined by $g(x) = 3x^2$ and the points where x = k and x = 4
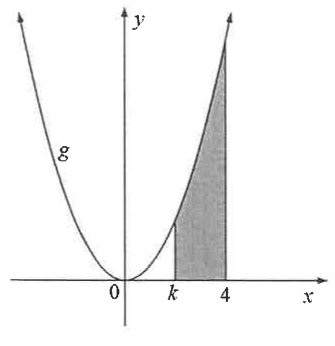
$ (14.1) \\[3ex] \boldsymbol{{Power\;\;Rule}} \\[3ex] \displaystyle\int x(x^2 + 6x)dx \\[3ex] = \displaystyle\int (x^3 + 6x^2)dx \\[3ex] = \dfrac{x^4}{4} + \dfrac{6x^3}{3} + C \\[5ex] = \dfrac{x^4}{4} + 2x^3 + C \\[5ex] (14.2) \\[3ex] \boldsymbol{{Special\;\;Integrals}} \\[3ex] \displaystyle\int a^x dx = \dfrac{a^x}{\ln a} + C \\[5ex] \displaystyle\int 3^x dx + \displaystyle\int \dfrac{1}{x} dx \\[5ex] = \dfrac{3^x}{\ln 3} + \ln x + C \\[5ex] (14.3) \\[3ex] Area = \displaystyle\int_{x_1}^{x_2} g(x) dx \\[3ex] 56 = \displaystyle\int_{k}^{4} 3x^2 dx \\[3ex] 56 = \displaystyle\int_{k}^{4} 3x^2 dx \\[3ex] 56 = \left[\dfrac{3x^3}{3}\right]_k^4 \\[5ex] 56 = [x^3]_k^4 \\[3ex] 56 = 4^3 - k^3 \\[3ex] k^3 = 4^3 - 56 \\[3ex] k^3 = 64 - 56 \\[3ex] k^3 = 8 \\[3ex] k = \sqrt[3]{8} \\[3ex] k = 2 $
$ (14.1) \;\;\; \displaystyle\int x(x^2 + 6x)dx \\[3ex] (14.2) \;\;\; \displaystyle\int \left(3^x + \dfrac{1}{x}\right)dx \\[5ex] $ (14.3) The sketch below represents the area bounded by the function g defined by $g(x) = 3x^2$ and the points where x = k and x = 4

$ (14.1) \\[3ex] \boldsymbol{{Power\;\;Rule}} \\[3ex] \displaystyle\int x(x^2 + 6x)dx \\[3ex] = \displaystyle\int (x^3 + 6x^2)dx \\[3ex] = \dfrac{x^4}{4} + \dfrac{6x^3}{3} + C \\[5ex] = \dfrac{x^4}{4} + 2x^3 + C \\[5ex] (14.2) \\[3ex] \boldsymbol{{Special\;\;Integrals}} \\[3ex] \displaystyle\int a^x dx = \dfrac{a^x}{\ln a} + C \\[5ex] \displaystyle\int 3^x dx + \displaystyle\int \dfrac{1}{x} dx \\[5ex] = \dfrac{3^x}{\ln 3} + \ln x + C \\[5ex] (14.3) \\[3ex] Area = \displaystyle\int_{x_1}^{x_2} g(x) dx \\[3ex] 56 = \displaystyle\int_{k}^{4} 3x^2 dx \\[3ex] 56 = \displaystyle\int_{k}^{4} 3x^2 dx \\[3ex] 56 = \left[\dfrac{3x^3}{3}\right]_k^4 \\[5ex] 56 = [x^3]_k^4 \\[3ex] 56 = 4^3 - k^3 \\[3ex] k^3 = 4^3 - 56 \\[3ex] k^3 = 64 - 56 \\[3ex] k^3 = 8 \\[3ex] k = \sqrt[3]{8} \\[3ex] k = 2 $
(15.) MEHA The gradient function of the curve f(x) is given by $f'(x) = x(3x -
2)$
Find the equation of the curve given that the x-intercept of f(x) is 2
$ f'(x) = x(3x - 2) \\[3ex] f(x) = \displaystyle \int f'(x) dx \\[5ex] f(x) = \displaystyle\int x(3x - 2) dx \\[5ex] f(x) = \displaystyle\int (3x^2 - 2x)dx \\[5ex] f(x) = \dfrac{3x^3}{3} - \dfrac{2x^2}{2} + C \\[5ex] f(x) = x^3 - x^2 + C \\[3ex] y = x^3 - x^2 + C \\[3ex]...y = f(x) \\[3ex] Point = x-intercept = (x, 0) = (2, 0) \\[3ex] \implies x = 2,\;\;y = 0 \\[3ex] 0 = 2^3 - 2^2 + C \\[3ex] 0 = 8 - 4 + C \\[3ex] 0 = 4 + C \\[3ex] 4 + C = 0 \\[3ex] C = -4 \\[3ex] y = x^3 - x^2 - 4 \\[3ex] \therefore f(x) = x^3 - x^2 - 4 $
Find the equation of the curve given that the x-intercept of f(x) is 2
$ f'(x) = x(3x - 2) \\[3ex] f(x) = \displaystyle \int f'(x) dx \\[5ex] f(x) = \displaystyle\int x(3x - 2) dx \\[5ex] f(x) = \displaystyle\int (3x^2 - 2x)dx \\[5ex] f(x) = \dfrac{3x^3}{3} - \dfrac{2x^2}{2} + C \\[5ex] f(x) = x^3 - x^2 + C \\[3ex] y = x^3 - x^2 + C \\[3ex]...y = f(x) \\[3ex] Point = x-intercept = (x, 0) = (2, 0) \\[3ex] \implies x = 2,\;\;y = 0 \\[3ex] 0 = 2^3 - 2^2 + C \\[3ex] 0 = 8 - 4 + C \\[3ex] 0 = 4 + C \\[3ex] 4 + C = 0 \\[3ex] C = -4 \\[3ex] y = x^3 - x^2 - 4 \\[3ex] \therefore f(x) = x^3 - x^2 - 4 $
(16.) KCSE Find the area enclosed by the curve $y = x^2 + 2x$ the straight lines x =
1, x = 3, and the x-axis.
$ x^2 + 2x = 0 \\[3ex] x(x + 2) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x + 2 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = -2 \\[3ex] $ The zeros of the function...where the graph include areas above or below the x-axis are x = 0 and x = -2
But we are asked to calculate the area between x = 1 and x = 3
Because 0 and -2 are not included in that range, we skip those areas and only focus on the area between x = 1 and x = 3
$ Area = \displaystyle\int_1^3 (x^2 + 2x) dx \\[5ex] Area = \left[\dfrac{x^3}{3} + \dfrac{2x^2}{2}\right]_1^3 \\[5ex] Area = \left[\dfrac{x^3}{3} + x^2\right]_1^3 \\[5ex] x = 3 \\[3ex] \dfrac{3^3}{3} + 3^2 \\[5ex] 9 + 9 \\[3ex] 18 \\[3ex] x = 1 \\[3ex] \dfrac{1^3}{3} + 1^2 \\[5ex] \dfrac{1}{3} + 1 \\[5ex] \dfrac{1 + 3}{3} \\[5ex] \dfrac{4}{3} \\[5ex] Area = 18 - \dfrac{4}{3} \\[5ex] Area = \dfrac{54 - 4}{3} \\[5ex] Area = \dfrac{50}{3}\;square\;\;units $
$ x^2 + 2x = 0 \\[3ex] x(x + 2) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x + 2 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = -2 \\[3ex] $ The zeros of the function...where the graph include areas above or below the x-axis are x = 0 and x = -2
But we are asked to calculate the area between x = 1 and x = 3
Because 0 and -2 are not included in that range, we skip those areas and only focus on the area between x = 1 and x = 3
$ Area = \displaystyle\int_1^3 (x^2 + 2x) dx \\[5ex] Area = \left[\dfrac{x^3}{3} + \dfrac{2x^2}{2}\right]_1^3 \\[5ex] Area = \left[\dfrac{x^3}{3} + x^2\right]_1^3 \\[5ex] x = 3 \\[3ex] \dfrac{3^3}{3} + 3^2 \\[5ex] 9 + 9 \\[3ex] 18 \\[3ex] x = 1 \\[3ex] \dfrac{1^3}{3} + 1^2 \\[5ex] \dfrac{1}{3} + 1 \\[5ex] \dfrac{1 + 3}{3} \\[5ex] \dfrac{4}{3} \\[5ex] Area = 18 - \dfrac{4}{3} \\[5ex] Area = \dfrac{54 - 4}{3} \\[5ex] Area = \dfrac{50}{3}\;square\;\;units $
(17.) MEHA Consider the function $g(x) = \dfrac{1}{2}x^3 + x^2 + 1$ and the shaded region
shown below.
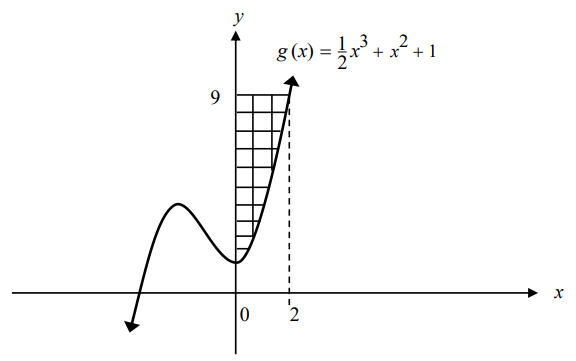
Calculate the area of the shaded region.
The shaded region is the area of the rectangle minus the area enclosed by the curve
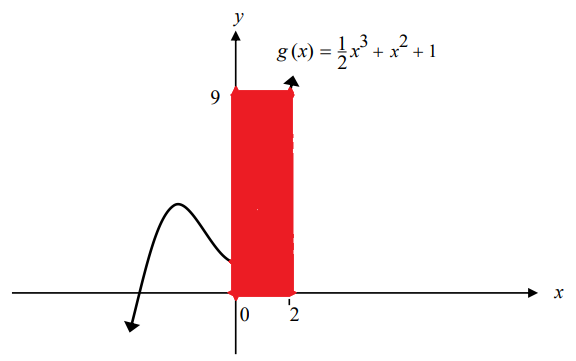
–
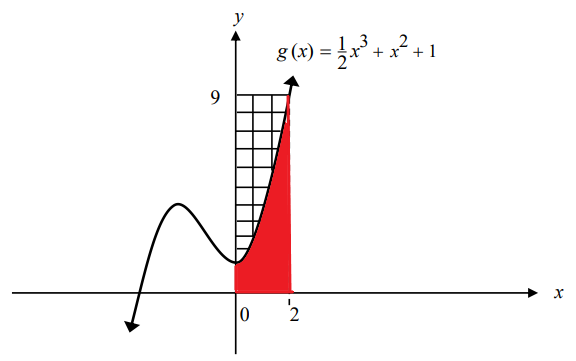
=
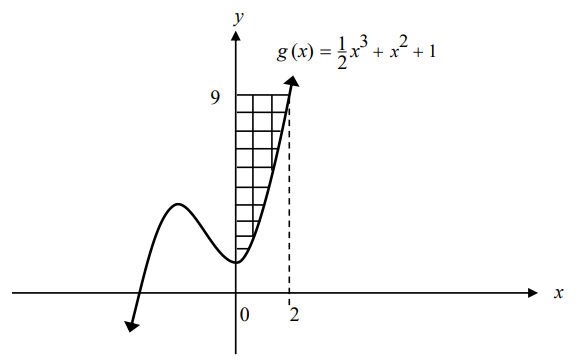
$ 1st:\;\;Area\;\;of\;\;the\;\;rectangle = 9 * 2 = 18\;square\;\;units \\[3ex] 2nd:\;\;Area\;\;enclosed\;\;by\;\;the\;\;curve \\[3ex] = \displaystyle\int_0^2 g(x) dx \\[3ex] = \displaystyle\int_0^2 \left(\dfrac{1}{2}x^3 + x^2 + 1\right) dx \\[5ex] = \left[\dfrac{1}{2} * \dfrac{x^4}{4} + \dfrac{x^3}{3} + x\right]_0^2 \\[5ex] = \left[\dfrac{x^4}{8} + \dfrac{x^3}{3} + x\right]_0^2 \\[5ex] = \left[\dfrac{2^4}{8} + \dfrac{2^3}{3} + 2\right] - \left[\dfrac{0^4}{8} + \dfrac{0^3}{3} + 0\right] \\[5ex] = \dfrac{16}{8} + \dfrac{8}{3} + \dfrac{2}{1} - 0 \\[5ex] = \dfrac{2}{1} + \dfrac{8}{3} + \dfrac{2}{1} \\[5ex] = \dfrac{6 + 8 + 6}{3} \\[5ex] = \dfrac{20}{3}\;square\;\;units \\[5ex] 3rd:\;\;Area\;\;of\;\;the\;\;shaded\;\;region \\[3ex] = 18 - \dfrac{20}{3} \\[5ex] = \dfrac{54 - 20}{3} \\[5ex] = \dfrac{34}{3}\;square\;\;units $

Calculate the area of the shaded region.
The shaded region is the area of the rectangle minus the area enclosed by the curve

–

=

$ 1st:\;\;Area\;\;of\;\;the\;\;rectangle = 9 * 2 = 18\;square\;\;units \\[3ex] 2nd:\;\;Area\;\;enclosed\;\;by\;\;the\;\;curve \\[3ex] = \displaystyle\int_0^2 g(x) dx \\[3ex] = \displaystyle\int_0^2 \left(\dfrac{1}{2}x^3 + x^2 + 1\right) dx \\[5ex] = \left[\dfrac{1}{2} * \dfrac{x^4}{4} + \dfrac{x^3}{3} + x\right]_0^2 \\[5ex] = \left[\dfrac{x^4}{8} + \dfrac{x^3}{3} + x\right]_0^2 \\[5ex] = \left[\dfrac{2^4}{8} + \dfrac{2^3}{3} + 2\right] - \left[\dfrac{0^4}{8} + \dfrac{0^3}{3} + 0\right] \\[5ex] = \dfrac{16}{8} + \dfrac{8}{3} + \dfrac{2}{1} - 0 \\[5ex] = \dfrac{2}{1} + \dfrac{8}{3} + \dfrac{2}{1} \\[5ex] = \dfrac{6 + 8 + 6}{3} \\[5ex] = \dfrac{20}{3}\;square\;\;units \\[5ex] 3rd:\;\;Area\;\;of\;\;the\;\;shaded\;\;region \\[3ex] = 18 - \dfrac{20}{3} \\[5ex] = \dfrac{54 - 20}{3} \\[5ex] = \dfrac{34}{3}\;square\;\;units $
(18.) (a.) Graph $f(x) = 5 - x^2$ and $g(x) = x^2 - 3$, shading the area enclosed.
(b.) Find the area of the shaded region.
$ f(x) \text{ and } g(x) \text{ are quadratic functions} \\[3ex] y = ax^2 + bx + c ...\text{Standard Form of a Quadratic Function} \\[3ex] (a.) \\[3ex] \underline{\text{Function}} \\[3ex] f(x) = 5 - x^2 \\[3ex] \underline{\text{Vertex}} \\[3ex] f(x) = -x^2 + 0x + 5 \\[3ex] a = -1 \\[3ex] b = 0 \\[3ex] c = 5 \\[3ex] x-\text{coordinate of Vertex} = -\dfrac{b}{2a} = -\dfrac{0}{2(-1)} = 0 \\[5ex] y-\text{coordinate of Vertex} = f(0) = 5 - 0^2 = 5 \\[3ex] Vertex = (0, 5) \\[5ex] \underline{\text{Intercepts}} \\[3ex] 0 = 5 - x^2 \\[3ex] x^2 = 5 \\[3ex] x = \pm\sqrt{5} \\[3ex] x-intercepts = (-\sqrt{5}, 0) \text{ and } (\sqrt{5}, 0) \\[5ex] f(0) = 5 \\[3ex] y-intercept = (0, 5) \\[5ex] \underline{\text{Function}} \\[3ex] g(x) = x^2 - 3 \\[3ex] \underline{\text{Vertex}} \\[3ex] g(x) = x^2 + 0x - 3 \\[3ex] a = 1 \\[3ex] b = 0 \\[3ex] c = -3 \\[3ex] x-\text{coordinate of Vertex} = -\dfrac{b}{2a} = -\dfrac{0}{2(1)} = 0 \\[5ex] y-\text{coordinate of Vertex} = g(0) = 0^2 - 3 = -3 \\[3ex] Vertex = (0, -3) \\[5ex] \underline{\text{Intercepts}} \\[3ex] 0 = x^2 - 3 \\[3ex] x^2 = 3 \\[3ex] x = \pm\sqrt{3} \\[3ex] x-intercepts = (-\sqrt{3}, 0) \text{ and } (\sqrt{3}, 0) \\[5ex] g(0) = -3 \\[3ex] y-intercept = (0, -3) \\[5ex] \underline{\text{Intersection of the Functions}} \\[3ex] f(x) = g(x) \\[3ex] 5 - x^2 = x^2 - 3 \\[3ex] 5 + 3 = x^2 + x^2 \\[3ex] 2x^2 = 8 \\[3ex] x^2 = \dfrac{8}{2} \\[5ex] x^2 = 4 \\[3ex] x = \pm\sqrt{4} \\[3ex] x = \pm 2 \\[3ex] f(-2) = 5 - (-2)^2 \\[3ex] f(-2) = 5 - 4 \\[3ex] f(-2) = 1 \\[3ex] f(2) = 5 - 2^2 \\[3ex] f(2) = 5 - 4 \\[3ex] f(2) = 1 \\[3ex] f(-2) = f(2) = g(-2) = g(2) = 1...\text{Graphs intersect at } -2 \text{ and } 2 \\[3ex] \text{Points of Intersection are: } (-2, 1) \text{ and } (2, 1) \\[3ex] $ The graphs of the functions are shown below:
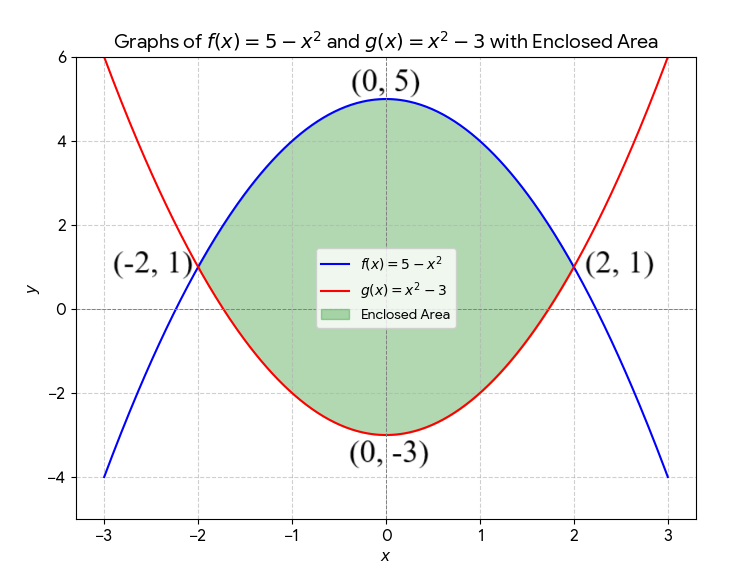
To find the area of the shaded region in the graphs, let us find the function that is above the other function within the points of intersection of the two graphs.
In the interval of the points of intersection, $[-2, 2]$, we can select 0 because $-2 \le 0 \le 2$
$ f(0) = 5 \\[3ex] g(0) = -3 \\[3ex] \implies f(x) \gt g(x)...\text{in the interval } [-2, 2] \\[3ex] \text{In the interval } [-2, 2]: \\[3ex] f(x) = \text{upper function} \\[3ex] g(x) = \text{lower function} \\[3ex] 2 = \text{upper limit of integration} \\[3ex] -2 = \text{lower limit of integration} \\[3ex] \underline{\text{Area of the shaded region}} \\[3ex] = \displaystyle\int_{-2}^2 [f(x) - g(x)] dx \\[3ex] = \displaystyle\int_{-2}^2 [(5 - x^2) - (x^2 - 3)] dx \\[3ex] = \displaystyle\int_{-2}^2 [5 - x^2 - x^2 + 3] dx \\[3ex] = \displaystyle\int_{-2}^2 (-2x^2 + 8) dx \\[3ex] = \left[-\dfrac{2x^3}{3} + 8x\right]_{-2}^2 \\[5ex] = \left[-\dfrac{2(2)^3}{3} + 8(2)\right] - \left[-\dfrac{2(-2)^3}{3} + 8(-2)\right] \\[5ex] = \left[-\dfrac{16}{3} + 16\right] - \left[-\dfrac{-16}{3} - 16\right] \\[5ex] = \left[\dfrac{-16}{3} + \dfrac{48}{3}\right] - \left[\dfrac{16}{3} - \dfrac{48}{3}\right] \\[5ex] = \dfrac{32}{3} - -\dfrac{32}{3} \\[5ex] = \dfrac{32}{3} + \dfrac{32}{3} \\[5ex] = \dfrac{64}{3}\text{ square units.} $
(b.) Find the area of the shaded region.
$ f(x) \text{ and } g(x) \text{ are quadratic functions} \\[3ex] y = ax^2 + bx + c ...\text{Standard Form of a Quadratic Function} \\[3ex] (a.) \\[3ex] \underline{\text{Function}} \\[3ex] f(x) = 5 - x^2 \\[3ex] \underline{\text{Vertex}} \\[3ex] f(x) = -x^2 + 0x + 5 \\[3ex] a = -1 \\[3ex] b = 0 \\[3ex] c = 5 \\[3ex] x-\text{coordinate of Vertex} = -\dfrac{b}{2a} = -\dfrac{0}{2(-1)} = 0 \\[5ex] y-\text{coordinate of Vertex} = f(0) = 5 - 0^2 = 5 \\[3ex] Vertex = (0, 5) \\[5ex] \underline{\text{Intercepts}} \\[3ex] 0 = 5 - x^2 \\[3ex] x^2 = 5 \\[3ex] x = \pm\sqrt{5} \\[3ex] x-intercepts = (-\sqrt{5}, 0) \text{ and } (\sqrt{5}, 0) \\[5ex] f(0) = 5 \\[3ex] y-intercept = (0, 5) \\[5ex] \underline{\text{Function}} \\[3ex] g(x) = x^2 - 3 \\[3ex] \underline{\text{Vertex}} \\[3ex] g(x) = x^2 + 0x - 3 \\[3ex] a = 1 \\[3ex] b = 0 \\[3ex] c = -3 \\[3ex] x-\text{coordinate of Vertex} = -\dfrac{b}{2a} = -\dfrac{0}{2(1)} = 0 \\[5ex] y-\text{coordinate of Vertex} = g(0) = 0^2 - 3 = -3 \\[3ex] Vertex = (0, -3) \\[5ex] \underline{\text{Intercepts}} \\[3ex] 0 = x^2 - 3 \\[3ex] x^2 = 3 \\[3ex] x = \pm\sqrt{3} \\[3ex] x-intercepts = (-\sqrt{3}, 0) \text{ and } (\sqrt{3}, 0) \\[5ex] g(0) = -3 \\[3ex] y-intercept = (0, -3) \\[5ex] \underline{\text{Intersection of the Functions}} \\[3ex] f(x) = g(x) \\[3ex] 5 - x^2 = x^2 - 3 \\[3ex] 5 + 3 = x^2 + x^2 \\[3ex] 2x^2 = 8 \\[3ex] x^2 = \dfrac{8}{2} \\[5ex] x^2 = 4 \\[3ex] x = \pm\sqrt{4} \\[3ex] x = \pm 2 \\[3ex] f(-2) = 5 - (-2)^2 \\[3ex] f(-2) = 5 - 4 \\[3ex] f(-2) = 1 \\[3ex] f(2) = 5 - 2^2 \\[3ex] f(2) = 5 - 4 \\[3ex] f(2) = 1 \\[3ex] f(-2) = f(2) = g(-2) = g(2) = 1...\text{Graphs intersect at } -2 \text{ and } 2 \\[3ex] \text{Points of Intersection are: } (-2, 1) \text{ and } (2, 1) \\[3ex] $ The graphs of the functions are shown below:

To find the area of the shaded region in the graphs, let us find the function that is above the other function within the points of intersection of the two graphs.
In the interval of the points of intersection, $[-2, 2]$, we can select 0 because $-2 \le 0 \le 2$
$ f(0) = 5 \\[3ex] g(0) = -3 \\[3ex] \implies f(x) \gt g(x)...\text{in the interval } [-2, 2] \\[3ex] \text{In the interval } [-2, 2]: \\[3ex] f(x) = \text{upper function} \\[3ex] g(x) = \text{lower function} \\[3ex] 2 = \text{upper limit of integration} \\[3ex] -2 = \text{lower limit of integration} \\[3ex] \underline{\text{Area of the shaded region}} \\[3ex] = \displaystyle\int_{-2}^2 [f(x) - g(x)] dx \\[3ex] = \displaystyle\int_{-2}^2 [(5 - x^2) - (x^2 - 3)] dx \\[3ex] = \displaystyle\int_{-2}^2 [5 - x^2 - x^2 + 3] dx \\[3ex] = \displaystyle\int_{-2}^2 (-2x^2 + 8) dx \\[3ex] = \left[-\dfrac{2x^3}{3} + 8x\right]_{-2}^2 \\[5ex] = \left[-\dfrac{2(2)^3}{3} + 8(2)\right] - \left[-\dfrac{2(-2)^3}{3} + 8(-2)\right] \\[5ex] = \left[-\dfrac{16}{3} + 16\right] - \left[-\dfrac{-16}{3} - 16\right] \\[5ex] = \left[\dfrac{-16}{3} + \dfrac{48}{3}\right] - \left[\dfrac{16}{3} - \dfrac{48}{3}\right] \\[5ex] = \dfrac{32}{3} - -\dfrac{32}{3} \\[5ex] = \dfrac{32}{3} + \dfrac{32}{3} \\[5ex] = \dfrac{64}{3}\text{ square units.} $
(19.) Consider a function $y = 3x^2 + 2x - 7$
Calculate the area enclosed by the function, the function, the x-axis and the vertical lines $a = 2$ and $b = 8$
Because $a = 2$ and $b = 8$ are vertical lines, we can say that $x = 2$ and $x = 8$
1st: Let us calculate the roots of the function to determine their position relative to the bounds, $x = 2$ and $x = 8$
$ y = 3x^2 + 2x - 7 \\[3ex] \text{Compare to the standard form: } y = ax^2 + bx + c \\[3ex] a = 3 \\[3ex] b = 2 \\[3ex] c = -7 \\[3ex] x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} ...\text{Quadratic Formula} \\[5ex] x = \dfrac{-2 \pm \sqrt{2^2 - 4(3)(-7)}}{2(3)} \\[5ex] x = \dfrac{-2 \pm \sqrt{4 + 84}}{6} \\[5ex] x = \dfrac{-2 \pm 9.38083152}{6} \\[5ex] x = \dfrac{7.38083152}{6} \hspace{1em}or\hspace{1em} x = -\dfrac{11.38083152}{2} \\[5ex] x = 1.230138587 \hspace{1em}or\hspace{1em} x = -1.896805253 \\[3ex] 1.230138587 \lt 2 \\[3ex] -1.896805253 \lt 2 \\[3ex] $ So, the interval [2, 8] lies to the right of the 1.230138587
2nd: Let us find the sign of y on the interval [2, 8]
$a = 3$ is positive (greater than zero)
This implies that the parabola opens upwards.
Because the interval lies to the right of both roots and $a \gt 0$, this implies that $y \gt 0$ throughout [2, 8]
But, if you still want to check, we can
When $x = 2$, $y = 3(2)^2 + 2(2) - 7$
$y \gt 0$
When $x = 8$, $y = 3(8)^2 + 2(8) - 7$
$y \gt 0$
Would you like to see it graphically?
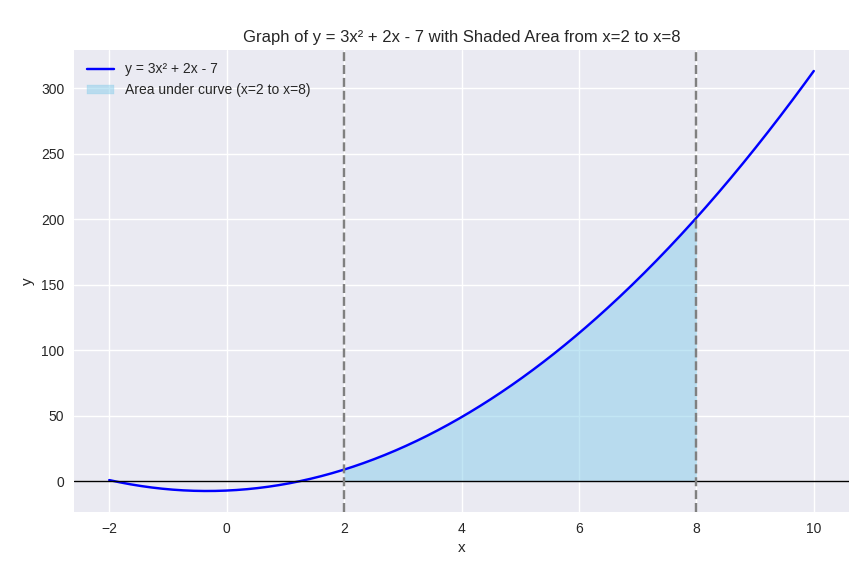
Source: copilot.com
3rd: We see that the area enclosed by the function, the function, the x-axis and the vertical lines $x = 2$ and $x = 8$ is the integral of the function at the bounds: lower limit of integration at 2 and the upper limit of integration at 8.
$ \displaystyle\int (3x^2 + 2x - 7) dx \\[5ex] = \dfrac{3x^3}{3} + \dfrac{2x^2}{2} - 7x + C \\[5ex] = x^3 + x^2 - 7x + C \\[5ex] \left[x^3 + x^2 - 7x\right]_2^8 \\[5ex] = [8^3 + 8^2 - 7(8)] - [2^3 + 2^2 - 7(2)] \\[3ex] = 520 - (-2) \\[3ex] = 522\text{ square units.} $
Calculate the area enclosed by the function, the function, the x-axis and the vertical lines $a = 2$ and $b = 8$
Because $a = 2$ and $b = 8$ are vertical lines, we can say that $x = 2$ and $x = 8$
1st: Let us calculate the roots of the function to determine their position relative to the bounds, $x = 2$ and $x = 8$
$ y = 3x^2 + 2x - 7 \\[3ex] \text{Compare to the standard form: } y = ax^2 + bx + c \\[3ex] a = 3 \\[3ex] b = 2 \\[3ex] c = -7 \\[3ex] x = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} ...\text{Quadratic Formula} \\[5ex] x = \dfrac{-2 \pm \sqrt{2^2 - 4(3)(-7)}}{2(3)} \\[5ex] x = \dfrac{-2 \pm \sqrt{4 + 84}}{6} \\[5ex] x = \dfrac{-2 \pm 9.38083152}{6} \\[5ex] x = \dfrac{7.38083152}{6} \hspace{1em}or\hspace{1em} x = -\dfrac{11.38083152}{2} \\[5ex] x = 1.230138587 \hspace{1em}or\hspace{1em} x = -1.896805253 \\[3ex] 1.230138587 \lt 2 \\[3ex] -1.896805253 \lt 2 \\[3ex] $ So, the interval [2, 8] lies to the right of the 1.230138587
2nd: Let us find the sign of y on the interval [2, 8]
$a = 3$ is positive (greater than zero)
This implies that the parabola opens upwards.
Because the interval lies to the right of both roots and $a \gt 0$, this implies that $y \gt 0$ throughout [2, 8]
But, if you still want to check, we can
When $x = 2$, $y = 3(2)^2 + 2(2) - 7$
$y \gt 0$
When $x = 8$, $y = 3(8)^2 + 2(8) - 7$
$y \gt 0$
Would you like to see it graphically?

Source: copilot.com
3rd: We see that the area enclosed by the function, the function, the x-axis and the vertical lines $x = 2$ and $x = 8$ is the integral of the function at the bounds: lower limit of integration at 2 and the upper limit of integration at 8.
$ \displaystyle\int (3x^2 + 2x - 7) dx \\[5ex] = \dfrac{3x^3}{3} + \dfrac{2x^2}{2} - 7x + C \\[5ex] = x^3 + x^2 - 7x + C \\[5ex] \left[x^3 + x^2 - 7x\right]_2^8 \\[5ex] = [8^3 + 8^2 - 7(8)] - [2^3 + 2^2 - 7(2)] \\[3ex] = 520 - (-2) \\[3ex] = 522\text{ square units.} $
(20.) WASSCE:FM Using the Trapezium Rule with seven ordinates, evaluate, correct to
three decimal places,
$
\displaystyle\int_{2.4}^{3.6} \dfrac{1}{\sqrt{x^2 - 2}} dx \\[5ex]
$
Because we are asked to round the final answer to three decimal places, it is okay to round intermediate values to at least six decimal places.
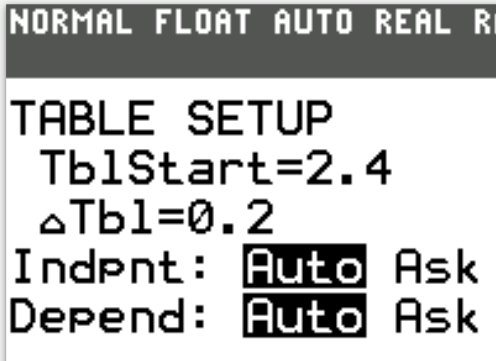
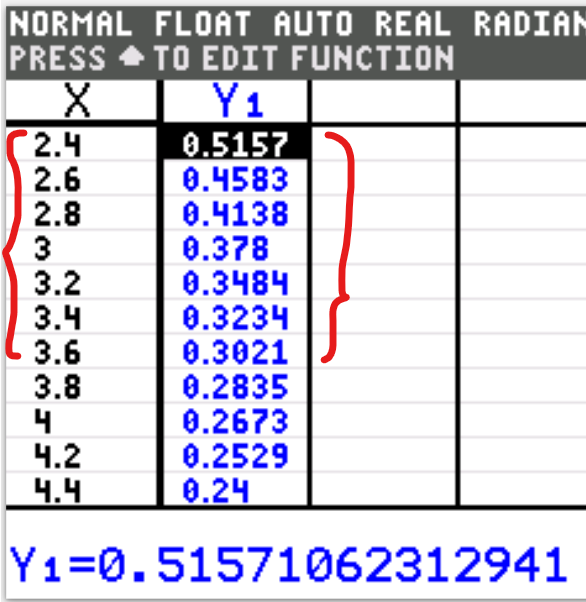
$ \dfrac{1}{\sqrt{x^2 - 2}} \\[5ex] r = \text{number of ordinates (nodes)} = 7 \\[3ex] n = \text{number of intervals} = 7 - 1 = 6 \\[5ex] \underline{\text{Interval Width}} \\[3ex] \Delta x = \dfrac{d - c}{n} \\[5ex] where: \\[3ex] c = \text{lower limit of integration} = 2.4 \\[3ex] d = \text{upper limit of integration} = 3.6 \\[3ex] \Delta x = \text{width of the interval} \\[3ex] \Delta x = \dfrac{3.6 - 2.4}{6} \\[5ex] = \dfrac{1.2}{6} \\[5ex] = 0.2 \\[5ex] \underline{\text{Nodes (Ordinates)}} \\[3ex] \text{The nodes are:} \\[3ex] x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7 \\[3ex] = 2.4, 2.4 + 0.2, 2.4 + 2(0.2), 2.4 + 3(0.2), 2.4 + 4(0.2), 2.4 + 5(0.2), 2.4 + 6(0.2) \\[3ex] = 2.4, 2.6, 2.8, 3, 3.2, 3.4, 3.6 \\[5ex] \underline{\text{Function Values}} \\[3ex] f(x_0), f(x_1), f(x_2), f(x_3), f(x_4), f(x_5), f(x_6), f(x_7) \\[3ex] f(2.4) = \dfrac{1}{\sqrt{(2.4)^2 - 2}} \approx 0.515711 \\[5ex] f(2.6) = \dfrac{1}{\sqrt{(2.6)^2 - 2}} \approx 0.458349 \\[5ex] f(2.8) = \dfrac{1}{\sqrt{(2.8)^2 - 2}} \approx 0.413803 \\[5ex] f(3) = \dfrac{1}{\sqrt{(3)^2 - 2}} \approx 0.377964 \\[5ex] f(3.2) = \dfrac{1}{\sqrt{(3.2)^2 - 2}} \approx 0.348367 \\[5ex] f(3.4) = \dfrac{1}{\sqrt{(3.4)^2 - 2}} \approx 0.323423 \\[5ex] f(3.6) = \dfrac{1}{\sqrt{(3.6)^2 - 2}} \approx 0.302061 \\[7ex] \underline{\text{Trapezium Rule}} \\[3ex] \text{Definite Integral} = \dfrac{\Delta x}{2} [f(x_0) + f(x_n) + 2(f(x_1) + f(x_2) + f(x_3) + ... + f(x_{n - 1}))] \\[5ex] = \dfrac{0.2}{2} [0.515711 + 0.302031 + 2(0.458349 + 0.413803 + 0.377964 + 0.348367 + 0.323423)] \\[5ex] = 0.1(4.661554) \\[3ex] = 0.4661554 \\[3ex] \approx 0.466 ...\text{to 3 decimal places} $
Directly (by Calculator): This is the exact answer.
Trapezium Rule gives an approximate.

Intermediate Steps:
Because we are asked to round the final answer to three decimal places, it is okay to round intermediate values to at least six decimal places.
$ \dfrac{1}{\sqrt{x^2 - 2}} \\[5ex] r = \text{number of ordinates (nodes)} = 7 \\[3ex] n = \text{number of intervals} = 7 - 1 = 6 \\[5ex] \underline{\text{Interval Width}} \\[3ex] \Delta x = \dfrac{d - c}{n} \\[5ex] where: \\[3ex] c = \text{lower limit of integration} = 2.4 \\[3ex] d = \text{upper limit of integration} = 3.6 \\[3ex] \Delta x = \text{width of the interval} \\[3ex] \Delta x = \dfrac{3.6 - 2.4}{6} \\[5ex] = \dfrac{1.2}{6} \\[5ex] = 0.2 \\[5ex] \underline{\text{Nodes (Ordinates)}} \\[3ex] \text{The nodes are:} \\[3ex] x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7 \\[3ex] = 2.4, 2.4 + 0.2, 2.4 + 2(0.2), 2.4 + 3(0.2), 2.4 + 4(0.2), 2.4 + 5(0.2), 2.4 + 6(0.2) \\[3ex] = 2.4, 2.6, 2.8, 3, 3.2, 3.4, 3.6 \\[5ex] \underline{\text{Function Values}} \\[3ex] f(x_0), f(x_1), f(x_2), f(x_3), f(x_4), f(x_5), f(x_6), f(x_7) \\[3ex] f(2.4) = \dfrac{1}{\sqrt{(2.4)^2 - 2}} \approx 0.515711 \\[5ex] f(2.6) = \dfrac{1}{\sqrt{(2.6)^2 - 2}} \approx 0.458349 \\[5ex] f(2.8) = \dfrac{1}{\sqrt{(2.8)^2 - 2}} \approx 0.413803 \\[5ex] f(3) = \dfrac{1}{\sqrt{(3)^2 - 2}} \approx 0.377964 \\[5ex] f(3.2) = \dfrac{1}{\sqrt{(3.2)^2 - 2}} \approx 0.348367 \\[5ex] f(3.4) = \dfrac{1}{\sqrt{(3.4)^2 - 2}} \approx 0.323423 \\[5ex] f(3.6) = \dfrac{1}{\sqrt{(3.6)^2 - 2}} \approx 0.302061 \\[7ex] \underline{\text{Trapezium Rule}} \\[3ex] \text{Definite Integral} = \dfrac{\Delta x}{2} [f(x_0) + f(x_n) + 2(f(x_1) + f(x_2) + f(x_3) + ... + f(x_{n - 1}))] \\[5ex] = \dfrac{0.2}{2} [0.515711 + 0.302031 + 2(0.458349 + 0.413803 + 0.377964 + 0.348367 + 0.323423)] \\[5ex] = 0.1(4.661554) \\[3ex] = 0.4661554 \\[3ex] \approx 0.466 ...\text{to 3 decimal places} $
Directly (by Calculator): This is the exact answer.
Trapezium Rule gives an approximate.

Intermediate Steps:



(21.) HSC (a) Determine the area between the parabola $y = x^2 - x + 3$ and the straight line
$y = x + 3$
(b) The area between the parabola $y = x^2 - x - 2$ and the straight line $y = x - 2$ is the same as the area determined in part (a).
Explain why this is the case.
$ (a) \\[3ex] \underline{Points\;\;of\;\;Intersection} \\[3ex] Parabola:\;\;y = x^2 - x + 3 \\[3ex] Straight\;\;Line:\;\; y = x + 3 \\[3ex] y = y \\[3ex] \implies \\[3ex] x^2 - x + 3 = x + 3 \\[3ex] x^2 - x + 3 - x - 3 = 0 \\[3ex] x^2 - 2x = 0 \\[3ex] x(x - 2) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x - 2 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 2 \\[3ex] \therefore limits\;\;of\;\;integration\;\;are:\;\; x = 0 \;\;\;AND\;\;\; x = 2 \\[3ex] \underline{Area\;\;enclosed\;\;by\;\;the\;\;Parabola\;\;and\;\;the\;\;Straight\;\;Line} \\[3ex] first\;\;function:\;\; y = x^2 - x + 3 \\[3ex] second\;\;function:\;\; y = x + 3 \\[3ex] first\;\;function - second\;\;function \\[3ex] = x^2 - x + 3 - (x + 3) \\[3ex] = x^2 - x + 3 - x - 3 \\[3ex] = x^2 - 2x \\[3ex] Area = \displaystyle\int_{lower\;\;limit}^{upper\;\;limit} (first\;\;function - second\;\;function) dx \\[5ex] = \displaystyle\int_{0}^{2} (x^2 - 2x) dx \\[5ex] = \left[\dfrac{x^3}{3} - \dfrac{2x^2}{2}\right]_0^2 \\[5ex] = \left[\dfrac{x^3}{3} - x^2\right]_0^2 \\[5ex] = \left[\dfrac{2^3}{3} - 2^2\right] - \left[\dfrac{0^3}{3} - 0^2\right] \\[5ex] = \left[\dfrac{8}{3} - \dfrac{4}{1}\right] - [0 - 0] \\[5ex] = \dfrac{8 - 12}{3} \\[5ex] = -\dfrac{4}{3} \\[5ex] But:\;\;Area\;\;cannot\;\;be\;\;negative \\[3ex] \therefore Area = \dfrac{4}{3}\;square\;\;units \\[5ex] (b) \\[3ex] \underline{Points\;\;of\;\;Intersection} \\[3ex] Parabola:\;\;y = x^2 - x - 2 \\[3ex] Straight\;\;Line:\;\; y = x - 2 \\[3ex] y = y \\[3ex] \implies \\[3ex] x^2 - x - 2 = x - 2 \\[3ex] x^2 - x - 2 - x + 2 = 0 \\[3ex] x^2 - 2x = 0 \\[3ex] x(x - 2) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x - 2 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 2 \\[3ex] $ These are the same points of intersection as part (a)
Also:
$ \underline{Area\;\;enclosed\;\;by\;\;the\;\;Parabola\;\;and\;\;the\;\;Straight\;\;Line} \\[3ex] first\;\;function:\;\; y = x^2 - x - 2 \\[3ex] second\;\;function:\;\; y = x - 2 \\[3ex] first\;\;function - second\;\;function \\[3ex] = x^2 - x - 2 - (x - 2) \\[3ex] = x^2 - x - 2 - x + 2 \\[3ex] = x^2 - 2x \\[3ex] $ The area enclosed is the same as part (a)
Because of the same points of intersection and the same areas enclosed, the area between the parabola and the straight line respectively for parts (a) and (b) are the same.
(b) The area between the parabola $y = x^2 - x - 2$ and the straight line $y = x - 2$ is the same as the area determined in part (a).
Explain why this is the case.
$ (a) \\[3ex] \underline{Points\;\;of\;\;Intersection} \\[3ex] Parabola:\;\;y = x^2 - x + 3 \\[3ex] Straight\;\;Line:\;\; y = x + 3 \\[3ex] y = y \\[3ex] \implies \\[3ex] x^2 - x + 3 = x + 3 \\[3ex] x^2 - x + 3 - x - 3 = 0 \\[3ex] x^2 - 2x = 0 \\[3ex] x(x - 2) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x - 2 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 2 \\[3ex] \therefore limits\;\;of\;\;integration\;\;are:\;\; x = 0 \;\;\;AND\;\;\; x = 2 \\[3ex] \underline{Area\;\;enclosed\;\;by\;\;the\;\;Parabola\;\;and\;\;the\;\;Straight\;\;Line} \\[3ex] first\;\;function:\;\; y = x^2 - x + 3 \\[3ex] second\;\;function:\;\; y = x + 3 \\[3ex] first\;\;function - second\;\;function \\[3ex] = x^2 - x + 3 - (x + 3) \\[3ex] = x^2 - x + 3 - x - 3 \\[3ex] = x^2 - 2x \\[3ex] Area = \displaystyle\int_{lower\;\;limit}^{upper\;\;limit} (first\;\;function - second\;\;function) dx \\[5ex] = \displaystyle\int_{0}^{2} (x^2 - 2x) dx \\[5ex] = \left[\dfrac{x^3}{3} - \dfrac{2x^2}{2}\right]_0^2 \\[5ex] = \left[\dfrac{x^3}{3} - x^2\right]_0^2 \\[5ex] = \left[\dfrac{2^3}{3} - 2^2\right] - \left[\dfrac{0^3}{3} - 0^2\right] \\[5ex] = \left[\dfrac{8}{3} - \dfrac{4}{1}\right] - [0 - 0] \\[5ex] = \dfrac{8 - 12}{3} \\[5ex] = -\dfrac{4}{3} \\[5ex] But:\;\;Area\;\;cannot\;\;be\;\;negative \\[3ex] \therefore Area = \dfrac{4}{3}\;square\;\;units \\[5ex] (b) \\[3ex] \underline{Points\;\;of\;\;Intersection} \\[3ex] Parabola:\;\;y = x^2 - x - 2 \\[3ex] Straight\;\;Line:\;\; y = x - 2 \\[3ex] y = y \\[3ex] \implies \\[3ex] x^2 - x - 2 = x - 2 \\[3ex] x^2 - x - 2 - x + 2 = 0 \\[3ex] x^2 - 2x = 0 \\[3ex] x(x - 2) = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x - 2 = 0 \\[3ex] x = 0 \;\;\;OR\;\;\; x = 2 \\[3ex] $ These are the same points of intersection as part (a)
Also:
$ \underline{Area\;\;enclosed\;\;by\;\;the\;\;Parabola\;\;and\;\;the\;\;Straight\;\;Line} \\[3ex] first\;\;function:\;\; y = x^2 - x - 2 \\[3ex] second\;\;function:\;\; y = x - 2 \\[3ex] first\;\;function - second\;\;function \\[3ex] = x^2 - x - 2 - (x - 2) \\[3ex] = x^2 - x - 2 - x + 2 \\[3ex] = x^2 - 2x \\[3ex] $ The area enclosed is the same as part (a)
Because of the same points of intersection and the same areas enclosed, the area between the parabola and the straight line respectively for parts (a) and (b) are the same.
(22.)
$ y = \dfrac{2x}{x^2 + 1} = \dfrac{p}{k} \\[5ex] p = 2x \\[3ex] p' = 2 \\[3ex] k = x^2 + 1 \\[3ex] k' = 2x \\[3ex] y' = \dfrac{kp' - pk'}{k^2} \\[5ex] y' = \dfrac{(x^2 + 1)(2) - 2x(2x)}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2x^2 + 2 - 4x^2}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2 - 2x^2}{(x^2 + 1)^2} \\[5ex] \text{Stationary Points} \\[3ex] y' = 0 \\[3ex] \implies \\[3ex] \dfrac{2 - 2x^2}{(x^2 + 1)^2} = 0 \\[5ex] 2 - 2x^2 = 0 \\[3ex] 2 = 2x^2 \\[3ex] 2x^2 = 2 \\[3ex] x^2 = \dfrac{2}{2} \\[5ex] x^2 = 1 \\[3ex] x = \pm \sqrt{1} \\[3ex] x = \pm 1 \\[3ex] y = \dfrac{2x}{x^2 + 1} \\[5ex] when\;\; x = 1 \\[3ex] y = \dfrac{2(1)}{1^2 + 1} \\[5ex] y = \dfrac{2}{1 + 1} \\[5ex] y = \dfrac{2}{2} \\[5ex] y = 1 \\[3ex] (x, y) \rightarrow (1, 1) \\[3ex] when\;\; x = -1 \\[3ex] y = \dfrac{2(-1)}{(-1)^2 + 1} \\[5ex] y = \dfrac{-2}{1 + 1} \\[5ex] y = \dfrac{-2}{2} \\[5ex] y = -1 \\[3ex] (x, y) \rightarrow (-1, -1) \\[3ex] $ The stationary points are: (1, 1) and (−1, −1)
$ y = \dfrac{2x}{x^2 + 1} = \dfrac{p}{k} \\[5ex] p = 2x \\[3ex] p' = 2 \\[3ex] k = x^2 + 1 \\[3ex] k' = 2x \\[3ex] y' = \dfrac{kp' - pk'}{k^2} \\[5ex] y' = \dfrac{(x^2 + 1)(2) - 2x(2x)}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2x^2 + 2 - 4x^2}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2 - 2x^2}{(x^2 + 1)^2} \\[5ex] \text{Stationary Points} \\[3ex] y' = 0 \\[3ex] \implies \\[3ex] \dfrac{2 - 2x^2}{(x^2 + 1)^2} = 0 \\[5ex] 2 - 2x^2 = 0 \\[3ex] 2 = 2x^2 \\[3ex] 2x^2 = 2 \\[3ex] x^2 = \dfrac{2}{2} \\[5ex] x^2 = 1 \\[3ex] x = \pm \sqrt{1} \\[3ex] x = \pm 1 \\[3ex] y = \dfrac{2x}{x^2 + 1} \\[5ex] when\;\; x = 1 \\[3ex] y = \dfrac{2(1)}{1^2 + 1} \\[5ex] y = \dfrac{2}{1 + 1} \\[5ex] y = \dfrac{2}{2} \\[5ex] y = 1 \\[3ex] (x, y) \rightarrow (1, 1) \\[3ex] when\;\; x = -1 \\[3ex] y = \dfrac{2(-1)}{(-1)^2 + 1} \\[5ex] y = \dfrac{-2}{1 + 1} \\[5ex] y = \dfrac{-2}{2} \\[5ex] y = -1 \\[3ex] (x, y) \rightarrow (-1, -1) \\[3ex] $ The stationary points are: (1, 1) and (−1, −1)
(23.)
(24.)
(25.)
$ (25.1) \\[3ex] Function:\;\;h(x) = ax^3 + bx^2 \\[3ex] For\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] y = h(x) = 32 \\[3ex] \implies \\[3ex] 32 = a(4)^3 + b(4)^2 \\[3ex] 32 = 64a + 16b \\[3ex] 64a + 16b = 32 \\[3ex] \implies \\[3ex] 4a + b = 2 ...eqn.(1) \\[3ex] Also: \\[3ex] h(x) = ax^3 + bx^2 \\[3ex] h'(x) = 3ax^2 + 2bx \\[3ex] At\;\;turning\;\;point,\;\;h'(x) = 0 \\[3ex] For\;\;Turning\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] \implies \\[3ex] h'(4) = 0 \\[3ex] h'(4) = 3a(4)^2 + 2b(4) = 0 \\[3ex] 48a + 8b = 0 \\[3ex] \implies \\[3ex] 6a + b = 0 ...eqn.(2) \\[3ex] eqn.(2) - eqn.(1) \\[3ex] 6a - 4a = 0 - 2 \\[3ex] 2a = -2 \\[3ex] a = -\dfrac{2}{2} \\[5ex] a = -1 \\[3ex] Substitute\;\;a = -1 \;\;into\;\;eqn.(1) \\[3ex] 4(-1) + b = 2 \\[3ex] -4 + b = 2 \\[3ex] b = 2 + 4 \\[3ex] b = 6 \\[3ex] \therefore h(x) = -x^3 + 6x^2 \\[3ex] (25.2) \\[3ex] A = x-intercept\;\;of\;\;h(x) \\[3ex] \implies \\[3ex] h(x) = 0 \\[3ex] -x^3 + 6x^2 = 0 \\[3ex] x^2(-x + 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; -x + 6 = 0 \\[3ex] x = \pm \sqrt{0} \;\;\;OR\;\;\; 6 = 0 + x \\[3ex] x = \pm 0 \;\;\;OR\;\;\; 6 = x \\[3ex] Based\;\;on\;\;the\;\;graph:\;\; x \ne \pm 0 \\[3ex] x = 6 \\[3ex] \therefore coordinates\;\;of\;\;A = (6, 0) \\[3ex] (25.3) \\[3ex] (25.3.1) \\[3ex] Based\;\;on\;\;the\;\;Graph \\[3ex] h(x)\uparrow for\;\; x \in (0, 4) \\[3ex] (25.3.2) \\[3ex] Based\;\;on\;\;the\;\;function \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h'(x) = -3x^2 + 12x \\[3ex] h''(x) = -6x + 12 \\[3ex] h''(x) = 0 \\[3ex] \implies \\[3ex] -6x + 12 = 0 \\[3ex] -6x = -12 \\[3ex] x = \dfrac{-12}{-6} \\[5ex] Inflection\;\;Point:\;\;x = 2 \\[3ex] Intervals:\;\; x \lt 2 \;\;and\;\; x \gt 2 \\[3ex] $
$ h(x)\frown for\;\; x \gt 2 \\[3ex] h(x)\frown for\;\; x \in (2, \infty) \\[3ex] (25.4) \\[3ex] -(x - 1)^3 + 6(x - 1)^2 - k = 0 \\[3ex] -(x - 1)^3 + 6(x - 1)^2 = k \\[3ex] k = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] \implies k = h(x - 1) \\[3ex] k = graph\;\;of\;\;h(x - 1) \\[3ex] 1st\;\;find\;\;the\;\;y-intercept...value\;\;of\;\;k\;\;when\;\;x = 0 \\[3ex] k = -(0 - 1)^3 + 6(0 - 1)^2 \\[3ex] k = -(-1)^3 + 6(-1)^2 \\[3ex] k = -(-1) + 6(1) \\[3ex] k = 1 + 6 \\[3ex] k = 7 \\[3ex] Negative\;\;root \implies x \lt 0 \\[3ex] When\;\;x \lt 0,\;\;k \lt 7 \\[3ex] Let\;\;us\;\;find\;\;the\;\;maximum\;\;value\;\;for\;\;the\;\;positive\;\;roots \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x - 1)' = -3(x - 1)^2 + 12(x - 1) \\[3ex] h(x - 1)' = 0 \\[3ex] \implies \\[3ex] -3(x - 1)^2 + 12(x - 1) = 0 \\[3ex] -3(x^2 - 2x + 1) + 12x - 12 = 0 \\[3ex] -3x^2 + 6x - 3 + 12x - 12 = 0 \\[3ex] -3x^2 + 18x - 15 = 0 \\[3ex] x^2 - 6x + 5 = 0 \\[3ex] (x - 5)(x - 1) = 0 \\[3ex] x - 5 = 0 \;\;\;OR\;\;\; x - 1 = 0 \\[3ex] x = 5 \;\;\;OR\;\;\; x = 1 \\[3ex] For\;\;x = 5 \\[3ex] h(x - 1) = -(5 - 1)^3 + 6(5 - 1)^2 \\[3ex] = -4^3 + 6(4^2) \\[3ex] = -64 + 6(16) \\[3ex] = -64 + 96 \\[3ex] = 32 \\[3ex] For\;\;x = 1 \\[3ex] h(x - 1) = -(1 - 1)^3 + 6(0 - 1)^2 \\[3ex] = -0^3 + 6(-1)^2 \\[3ex] = 0 + 6(1) \\[3ex] = 0 + 6 \\[3ex] = 6 \\[3ex] Maximum\;\;value = 32 \\[3ex] \implies \\[3ex] 7 \lt k \lt 32 $
$ (25.1) \\[3ex] Function:\;\;h(x) = ax^3 + bx^2 \\[3ex] For\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] y = h(x) = 32 \\[3ex] \implies \\[3ex] 32 = a(4)^3 + b(4)^2 \\[3ex] 32 = 64a + 16b \\[3ex] 64a + 16b = 32 \\[3ex] \implies \\[3ex] 4a + b = 2 ...eqn.(1) \\[3ex] Also: \\[3ex] h(x) = ax^3 + bx^2 \\[3ex] h'(x) = 3ax^2 + 2bx \\[3ex] At\;\;turning\;\;point,\;\;h'(x) = 0 \\[3ex] For\;\;Turning\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] \implies \\[3ex] h'(4) = 0 \\[3ex] h'(4) = 3a(4)^2 + 2b(4) = 0 \\[3ex] 48a + 8b = 0 \\[3ex] \implies \\[3ex] 6a + b = 0 ...eqn.(2) \\[3ex] eqn.(2) - eqn.(1) \\[3ex] 6a - 4a = 0 - 2 \\[3ex] 2a = -2 \\[3ex] a = -\dfrac{2}{2} \\[5ex] a = -1 \\[3ex] Substitute\;\;a = -1 \;\;into\;\;eqn.(1) \\[3ex] 4(-1) + b = 2 \\[3ex] -4 + b = 2 \\[3ex] b = 2 + 4 \\[3ex] b = 6 \\[3ex] \therefore h(x) = -x^3 + 6x^2 \\[3ex] (25.2) \\[3ex] A = x-intercept\;\;of\;\;h(x) \\[3ex] \implies \\[3ex] h(x) = 0 \\[3ex] -x^3 + 6x^2 = 0 \\[3ex] x^2(-x + 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; -x + 6 = 0 \\[3ex] x = \pm \sqrt{0} \;\;\;OR\;\;\; 6 = 0 + x \\[3ex] x = \pm 0 \;\;\;OR\;\;\; 6 = x \\[3ex] Based\;\;on\;\;the\;\;graph:\;\; x \ne \pm 0 \\[3ex] x = 6 \\[3ex] \therefore coordinates\;\;of\;\;A = (6, 0) \\[3ex] (25.3) \\[3ex] (25.3.1) \\[3ex] Based\;\;on\;\;the\;\;Graph \\[3ex] h(x)\uparrow for\;\; x \in (0, 4) \\[3ex] (25.3.2) \\[3ex] Based\;\;on\;\;the\;\;function \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h'(x) = -3x^2 + 12x \\[3ex] h''(x) = -6x + 12 \\[3ex] h''(x) = 0 \\[3ex] \implies \\[3ex] -6x + 12 = 0 \\[3ex] -6x = -12 \\[3ex] x = \dfrac{-12}{-6} \\[5ex] Inflection\;\;Point:\;\;x = 2 \\[3ex] Intervals:\;\; x \lt 2 \;\;and\;\; x \gt 2 \\[3ex] $
| Interval | $x \lt 2$ | $x \gt 2$ |
| Test Value | $x = 1$ | $x = 3$ |
| Sign Test | $$ -6(1) + 12 \\[3ex] -6 + 12 = 6 \\[3ex] 6 \gt 0 \\[3ex] positive $$ | $$ -6(3) + 12 \\[3ex] -18 + 12 = -6 \\[3ex] -6 \lt 0 \\[3ex] negative $$ |
| Conclusion | Concave up | Concave down |
$ h(x)\frown for\;\; x \gt 2 \\[3ex] h(x)\frown for\;\; x \in (2, \infty) \\[3ex] (25.4) \\[3ex] -(x - 1)^3 + 6(x - 1)^2 - k = 0 \\[3ex] -(x - 1)^3 + 6(x - 1)^2 = k \\[3ex] k = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] \implies k = h(x - 1) \\[3ex] k = graph\;\;of\;\;h(x - 1) \\[3ex] 1st\;\;find\;\;the\;\;y-intercept...value\;\;of\;\;k\;\;when\;\;x = 0 \\[3ex] k = -(0 - 1)^3 + 6(0 - 1)^2 \\[3ex] k = -(-1)^3 + 6(-1)^2 \\[3ex] k = -(-1) + 6(1) \\[3ex] k = 1 + 6 \\[3ex] k = 7 \\[3ex] Negative\;\;root \implies x \lt 0 \\[3ex] When\;\;x \lt 0,\;\;k \lt 7 \\[3ex] Let\;\;us\;\;find\;\;the\;\;maximum\;\;value\;\;for\;\;the\;\;positive\;\;roots \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x - 1)' = -3(x - 1)^2 + 12(x - 1) \\[3ex] h(x - 1)' = 0 \\[3ex] \implies \\[3ex] -3(x - 1)^2 + 12(x - 1) = 0 \\[3ex] -3(x^2 - 2x + 1) + 12x - 12 = 0 \\[3ex] -3x^2 + 6x - 3 + 12x - 12 = 0 \\[3ex] -3x^2 + 18x - 15 = 0 \\[3ex] x^2 - 6x + 5 = 0 \\[3ex] (x - 5)(x - 1) = 0 \\[3ex] x - 5 = 0 \;\;\;OR\;\;\; x - 1 = 0 \\[3ex] x = 5 \;\;\;OR\;\;\; x = 1 \\[3ex] For\;\;x = 5 \\[3ex] h(x - 1) = -(5 - 1)^3 + 6(5 - 1)^2 \\[3ex] = -4^3 + 6(4^2) \\[3ex] = -64 + 6(16) \\[3ex] = -64 + 96 \\[3ex] = 32 \\[3ex] For\;\;x = 1 \\[3ex] h(x - 1) = -(1 - 1)^3 + 6(0 - 1)^2 \\[3ex] = -0^3 + 6(-1)^2 \\[3ex] = 0 + 6(1) \\[3ex] = 0 + 6 \\[3ex] = 6 \\[3ex] Maximum\;\;value = 32 \\[3ex] \implies \\[3ex] 7 \lt k \lt 32 $
(26.)
(27.)
(28.)
(29.)
$ (a.) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = 7x^{-1} - 7\ln x \\[3ex] f'(x) = -7x^-2 - \left[7\left(\dfrac{1}{x}\right) + \ln x(0)\right] \\[5ex] f'(x) = -7x^{-2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] Simplify\;\;f(x)\;\;and\;\;f'(x) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = \dfrac{7 - 7x\ln x}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7 - 7x}{x^2} \\[5ex] \dfrac{f(x)}{f'(x)} \\[5ex] = f(x) \div f'(x) \\[3ex] = \dfrac{7 - 7x\ln x}{x} \div \dfrac{-7 - 7x}{x^2} \\[5ex] = \dfrac{7 - 7x\ln x}{x} * \dfrac{x^2}{-7 - 7x} \\[5ex] = \dfrac{7(1 - x\ln x)}{x} * \dfrac{x^2}{-7(1 + x)} \\[5ex] = \dfrac{x(1 - x\ln x)}{-(1 + x)} \\[5ex] = \dfrac{x - x^2\ln x}{-(1 + x)} \\[5ex] = -\dfrac{(x - x^2\ln x)}{1 + x} \\[5ex] = \dfrac{-x + x^2\ln x}{x + 1} \\[5ex] = \dfrac{x^2\ln x - x}{x + 1} \\[5ex] x - \dfrac{f(x)}{f'(x)} \\[5ex] = x - \dfrac{x^2\ln x - x}{x + 1} \\[5ex] = \dfrac{x(x + 1) - (x^2\ln x - x)}{x + 1} \\[5ex] = \dfrac{x^2 + x - x^2\ln x + x}{x + 1} \\[5ex] = \dfrac{x^2 + 2x - x^2\ln x}{x + 1} \\[5ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = \dfrac{x_n^2 + 2x_n - x_n^2\ln x_n}{x_n + 1} \\[5ex] x_1 = 1 \\[3ex] \implies \\[3ex] x_2 = \dfrac{x_1^2 + 2x_1 - x_1^2\ln x_1}{x_1 + 1} \\[5ex] x_2 = \dfrac{1^2 + 2(1) - 1^2 * \ln(1)}{1 + 1} \\[5ex] x_2 = \dfrac{1 + 2 - 1 * 0}{2} \\[5ex] x_2 = \dfrac{1 + 2 - 0}{2} \\[5ex] x_2 = \dfrac{3}{2} \\[7ex] x_3 = \dfrac{x_2^2 + 2x_2 - x_2^2\ln x_2}{x_2 + 1} \\[5ex] \underline{Numerator} \\[3ex] x_2^2 + 2x_2 - x_2^2\ln x_2 \\[3ex] = \left(\dfrac{3}{2}\right)^2 + 2 * \dfrac{3}{2} - \left(\dfrac{3}{2}\right)^2 * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{9}{4} + 3 - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] \underline{Denominator} \\[3ex] x_2 + 1 \\[3ex] = \dfrac{3}{2} + 1 \\[5ex] = \dfrac{3 + 2}{2} \\[5ex] = \dfrac{5}{2} \\[5ex] Numerator \div Denominator \\[3ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \div \dfrac{5}{2} \\[5ex] = \dfrac{1}{4}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] * \dfrac{2}{5} \\[5ex] = \dfrac{1}{10}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] \\[5ex] = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] \therefore x_3 = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] (b.) \\[3ex] x_3 = 2.1 - (0.9 * \ln(1.5)) \\[3ex] x_3 = 1.735081403 \\[3ex] $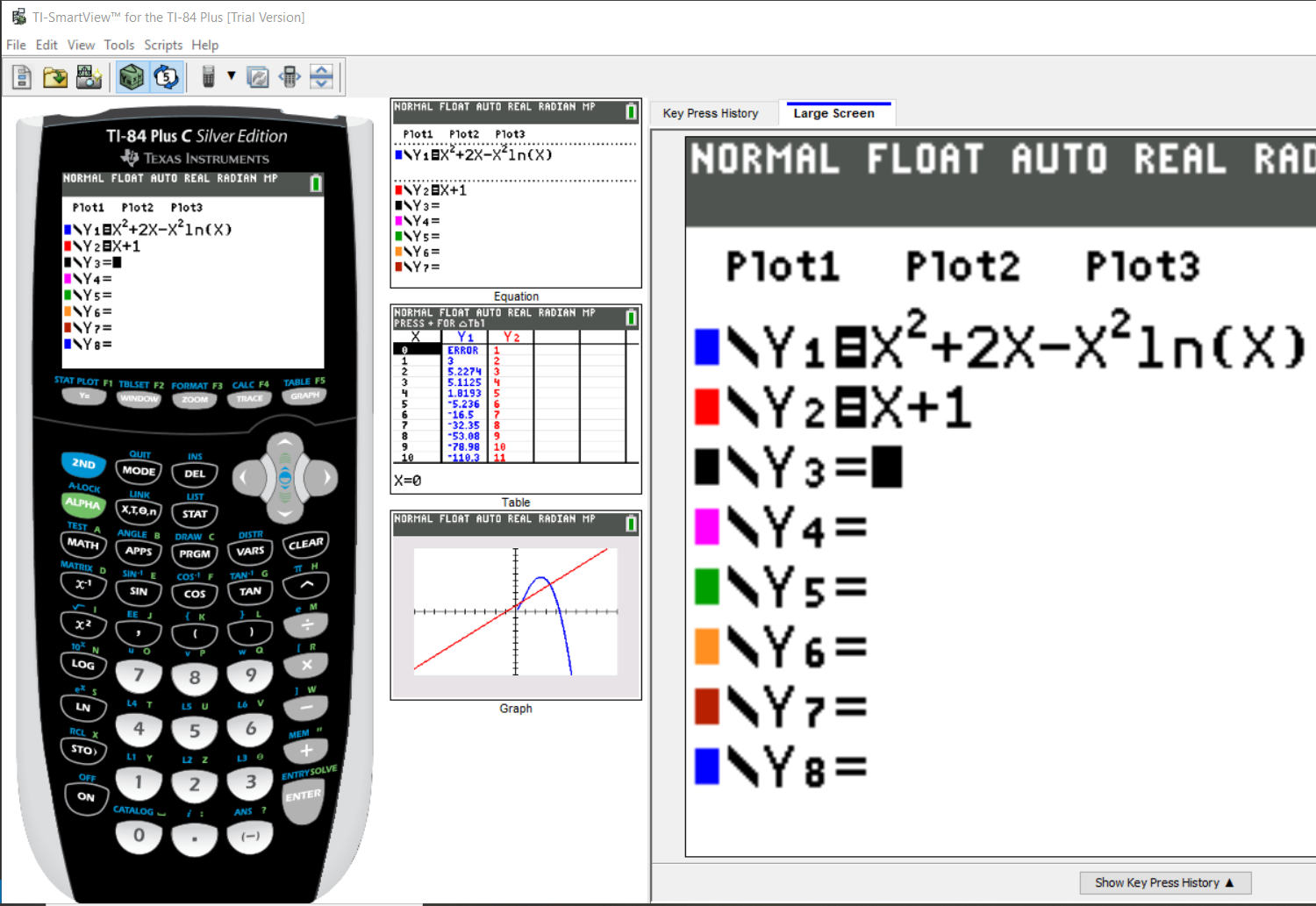
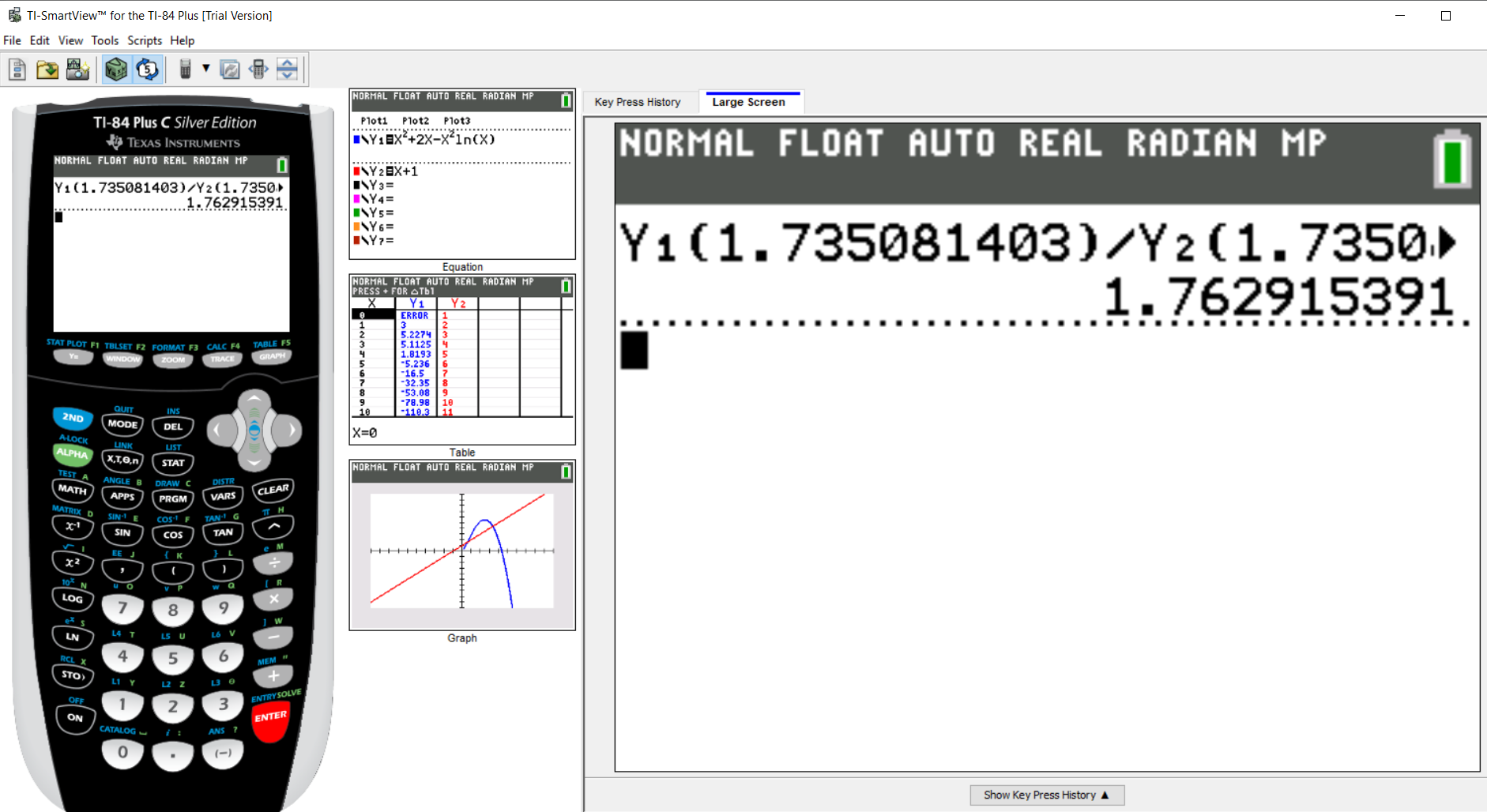
$ x_4 = 1.762915391 \\[3ex] $
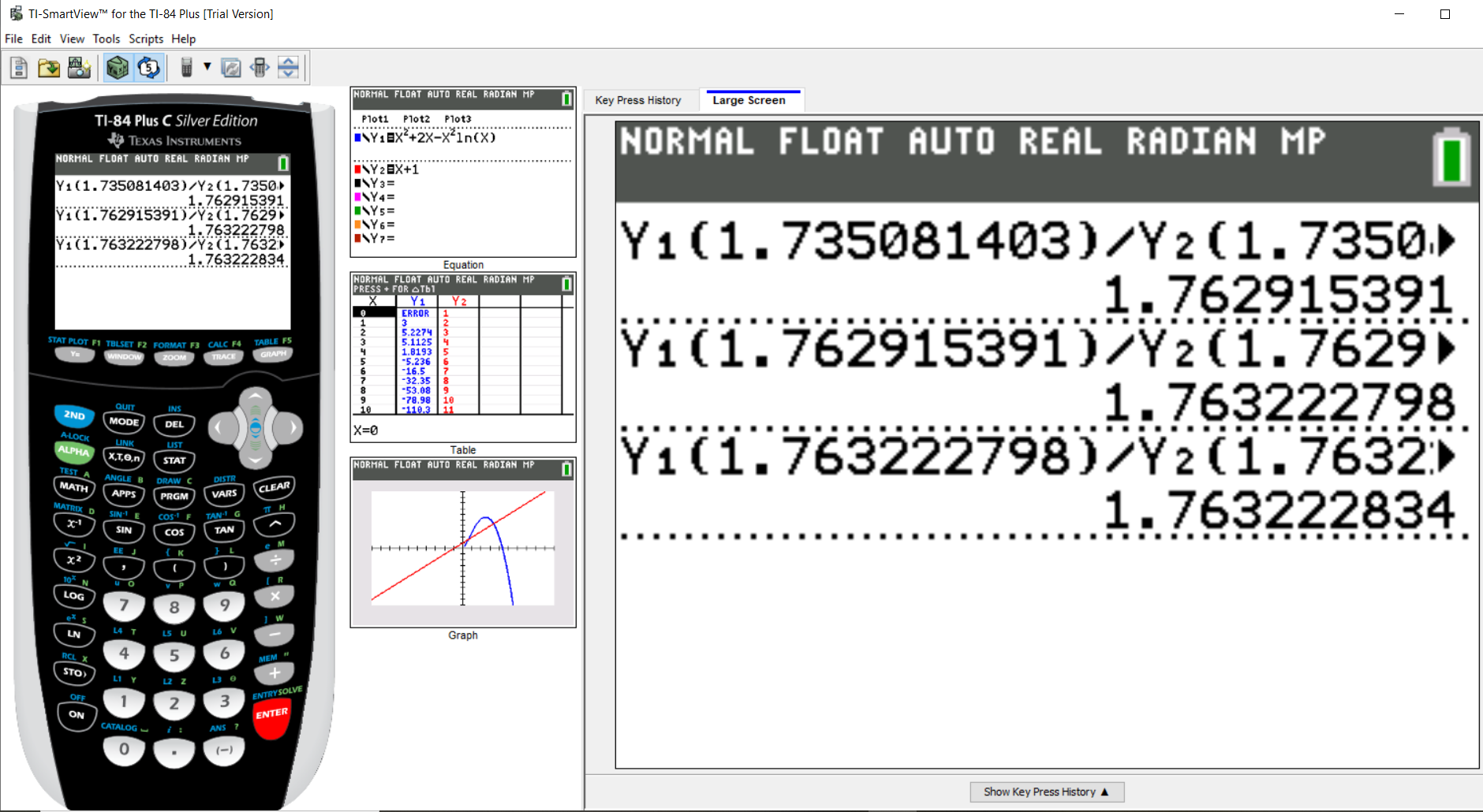
$ x_5 = 1.763222798 \\[3ex] x_6 = 1.763222834 \\[3ex] Because\;\;x_5 \approx x_6...STOP $
$ (a.) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = 7x^{-1} - 7\ln x \\[3ex] f'(x) = -7x^-2 - \left[7\left(\dfrac{1}{x}\right) + \ln x(0)\right] \\[5ex] f'(x) = -7x^{-2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] Simplify\;\;f(x)\;\;and\;\;f'(x) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = \dfrac{7 - 7x\ln x}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7 - 7x}{x^2} \\[5ex] \dfrac{f(x)}{f'(x)} \\[5ex] = f(x) \div f'(x) \\[3ex] = \dfrac{7 - 7x\ln x}{x} \div \dfrac{-7 - 7x}{x^2} \\[5ex] = \dfrac{7 - 7x\ln x}{x} * \dfrac{x^2}{-7 - 7x} \\[5ex] = \dfrac{7(1 - x\ln x)}{x} * \dfrac{x^2}{-7(1 + x)} \\[5ex] = \dfrac{x(1 - x\ln x)}{-(1 + x)} \\[5ex] = \dfrac{x - x^2\ln x}{-(1 + x)} \\[5ex] = -\dfrac{(x - x^2\ln x)}{1 + x} \\[5ex] = \dfrac{-x + x^2\ln x}{x + 1} \\[5ex] = \dfrac{x^2\ln x - x}{x + 1} \\[5ex] x - \dfrac{f(x)}{f'(x)} \\[5ex] = x - \dfrac{x^2\ln x - x}{x + 1} \\[5ex] = \dfrac{x(x + 1) - (x^2\ln x - x)}{x + 1} \\[5ex] = \dfrac{x^2 + x - x^2\ln x + x}{x + 1} \\[5ex] = \dfrac{x^2 + 2x - x^2\ln x}{x + 1} \\[5ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = \dfrac{x_n^2 + 2x_n - x_n^2\ln x_n}{x_n + 1} \\[5ex] x_1 = 1 \\[3ex] \implies \\[3ex] x_2 = \dfrac{x_1^2 + 2x_1 - x_1^2\ln x_1}{x_1 + 1} \\[5ex] x_2 = \dfrac{1^2 + 2(1) - 1^2 * \ln(1)}{1 + 1} \\[5ex] x_2 = \dfrac{1 + 2 - 1 * 0}{2} \\[5ex] x_2 = \dfrac{1 + 2 - 0}{2} \\[5ex] x_2 = \dfrac{3}{2} \\[7ex] x_3 = \dfrac{x_2^2 + 2x_2 - x_2^2\ln x_2}{x_2 + 1} \\[5ex] \underline{Numerator} \\[3ex] x_2^2 + 2x_2 - x_2^2\ln x_2 \\[3ex] = \left(\dfrac{3}{2}\right)^2 + 2 * \dfrac{3}{2} - \left(\dfrac{3}{2}\right)^2 * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{9}{4} + 3 - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] \underline{Denominator} \\[3ex] x_2 + 1 \\[3ex] = \dfrac{3}{2} + 1 \\[5ex] = \dfrac{3 + 2}{2} \\[5ex] = \dfrac{5}{2} \\[5ex] Numerator \div Denominator \\[3ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \div \dfrac{5}{2} \\[5ex] = \dfrac{1}{4}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] * \dfrac{2}{5} \\[5ex] = \dfrac{1}{10}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] \\[5ex] = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] \therefore x_3 = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] (b.) \\[3ex] x_3 = 2.1 - (0.9 * \ln(1.5)) \\[3ex] x_3 = 1.735081403 \\[3ex] $


$ x_4 = 1.762915391 \\[3ex] $

$ x_5 = 1.763222798 \\[3ex] x_6 = 1.763222834 \\[3ex] Because\;\;x_5 \approx x_6...STOP $
(30.)