Solved Examples: Applications of Derivatives
(1.) JAMB Find the maximum value of $y$ in the equation $y = 1 - 2x - 3x^2$
$ A.\:\: \dfrac{4}{3} \\[5ex] B.\:\: \dfrac{5}{4} \\[5ex] C.\:\: \dfrac{3}{4} \\[5ex] D.\:\: \dfrac{5}{3} \\[5ex] $
There are at least two appraches that we can use to solve the question: Derivatives and Vertex Formula
Derivatives: First Derivative Test
The maximum value is the $y-value$
The derivative is used to find the maximum value.
This is our first approach.
First, find the derivative.
Second, set it to zero and solve for $x$.
Third, substitute the value of $x$ in the function in order to find the $y$
Vertex Formula
The function is a quadratic function.
So, we can find the vertex of the parabola.
This is our second approach.
Use whichever approach you prefer: that you feel is fast and accurate.
$ \underline{\text{First Approach: Derivatives: First Derivative Test}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] \dfrac{dy}{dx} = -2 - 6x \\[5ex] Set\:\:\dfrac{dy}{dx} = 0 \\[5ex] -2 - 6x = 0 \\[3ex] -2 = 6x \\[3ex] 6x = -2 \\[3ex] x = -\dfrac{2}{6} \\[5ex] x = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} \\[5ex] \underline{\text{Second Approach: Vertex Formula}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] y = -3x^2 - 2x + 1 \\[3ex] y = ax^2 + bx + c \\[3ex] \text{Compare} \\[3ex] a = -3 \\[3ex] b = -2 \\[3ex] Vertex = \left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right) \\[5ex] x = -\dfrac{b}{2a} = \dfrac{-(-2)}{2(-3)} = \dfrac{2}{-6} = -\dfrac{2}{6} = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} $
$ A.\:\: \dfrac{4}{3} \\[5ex] B.\:\: \dfrac{5}{4} \\[5ex] C.\:\: \dfrac{3}{4} \\[5ex] D.\:\: \dfrac{5}{3} \\[5ex] $
There are at least two appraches that we can use to solve the question: Derivatives and Vertex Formula
Derivatives: First Derivative Test
The maximum value is the $y-value$
The derivative is used to find the maximum value.
This is our first approach.
First, find the derivative.
Second, set it to zero and solve for $x$.
Third, substitute the value of $x$ in the function in order to find the $y$
Vertex Formula
The function is a quadratic function.
So, we can find the vertex of the parabola.
This is our second approach.
Use whichever approach you prefer: that you feel is fast and accurate.
$ \underline{\text{First Approach: Derivatives: First Derivative Test}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] \dfrac{dy}{dx} = -2 - 6x \\[5ex] Set\:\:\dfrac{dy}{dx} = 0 \\[5ex] -2 - 6x = 0 \\[3ex] -2 = 6x \\[3ex] 6x = -2 \\[3ex] x = -\dfrac{2}{6} \\[5ex] x = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} \\[5ex] \underline{\text{Second Approach: Vertex Formula}} \\[3ex] y = 1 - 2x - 3x^2 \\[3ex] y = -3x^2 - 2x + 1 \\[3ex] y = ax^2 + bx + c \\[3ex] \text{Compare} \\[3ex] a = -3 \\[3ex] b = -2 \\[3ex] Vertex = \left(-\dfrac{b}{2a}, f\left(-\dfrac{b}{2a}\right)\right) \\[5ex] x = -\dfrac{b}{2a} = \dfrac{-(-2)}{2(-3)} = \dfrac{2}{-6} = -\dfrac{2}{6} = -\dfrac{1}{3} \\[5ex] \text{Substitute for x in the function} \\[3ex] y = 1 - 2\left(-\dfrac{1}{3}\right) - 3\left(-\dfrac{1}{3}\right)^2 \\[5ex] y = 1 + \dfrac{2}{3} - 3\left(-\dfrac{1}{3}\right)\left(-\dfrac{1}{3}\right) \\[5ex] y = \dfrac{3}{3} + \dfrac{2}{3} - \dfrac{1}{3} \\[5ex] y = \dfrac{3 + 2 - 1}{3} \\[5ex] y = \dfrac{5}{3} $
(2.) JAMB If the gradient of the curve $y = 2kx^2 + x + 1$ at $x = 1$ is $9$, find $k$
$ A.\:\: 4 \\[3ex] B.\:\: 3 \\[3ex] C.\:\: 2 \\[3ex] D.\:\: 1 \\[3ex] $
The gradient(slope) of the tangent line is the derivative
$ y = 2kx^2 + x + 1 \:\:at\:\:x = 1 \\[3ex] \dfrac{dy}{dx} = 4kx + 1 \\[5ex] At\:\: x = 1, \:\:\dfrac{dy}{dx} = 9 \\[5ex] \dfrac{dy}{dx}\Big|_{x = 1} = 4 * k * 1 + 1 = 9 \\[5ex] 4k + 1 = 9 \\[3ex] 4k = 9 - 1 \\[3ex] 4k = 8 \\[3ex] k = \dfrac{8}{4} \\[5ex] k = 2 $
$ A.\:\: 4 \\[3ex] B.\:\: 3 \\[3ex] C.\:\: 2 \\[3ex] D.\:\: 1 \\[3ex] $
The gradient(slope) of the tangent line is the derivative
$ y = 2kx^2 + x + 1 \:\:at\:\:x = 1 \\[3ex] \dfrac{dy}{dx} = 4kx + 1 \\[5ex] At\:\: x = 1, \:\:\dfrac{dy}{dx} = 9 \\[5ex] \dfrac{dy}{dx}\Big|_{x = 1} = 4 * k * 1 + 1 = 9 \\[5ex] 4k + 1 = 9 \\[3ex] 4k = 9 - 1 \\[3ex] 4k = 8 \\[3ex] k = \dfrac{8}{4} \\[5ex] k = 2 $
(3.) JAMB Find the slope of the curve $y = 2x^2 + 5x - 3$ at $(1, 4)$
$ A.\:\: 9 \\[3ex] B.\:\: 7 \\[3ex] C.\:\: 6 \\[3ex] D.\:\: 4 \\[3ex] $
The slope is the derivative
Power Rule
$ y = 2x^2 + 5x - 3 \\[3ex] y' = 4x + 5 \\[3ex] (1, 4) \rightarrow x = 1, y = 4 \\[3ex] y' = 4(1) + 5 \\[3ex] y' = 4 + 5 \\[3ex] y' = 9 $
$ A.\:\: 9 \\[3ex] B.\:\: 7 \\[3ex] C.\:\: 6 \\[3ex] D.\:\: 4 \\[3ex] $
The slope is the derivative
Power Rule
$ y = 2x^2 + 5x - 3 \\[3ex] y' = 4x + 5 \\[3ex] (1, 4) \rightarrow x = 1, y = 4 \\[3ex] y' = 4(1) + 5 \\[3ex] y' = 4 + 5 \\[3ex] y' = 9 $
(4.) USSCE: Advance Mathematics Paper 1 Find the gradient of the tangent line to the graph of
$y = 3x^2 - x + 1$ at the point where $x = -1$
$ y = 3x^2 - x + 1 \\[3ex] y' = 6x - 1 \\[3ex] \text{gradient} = y'\;\;@\;\;x = -1 \\[3ex] = 6(-1) - 1 \\[3ex] = -6 - 1 \\[3ex] = -7 $
$ y = 3x^2 - x + 1 \\[3ex] y' = 6x - 1 \\[3ex] \text{gradient} = y'\;\;@\;\;x = -1 \\[3ex] = 6(-1) - 1 \\[3ex] = -6 - 1 \\[3ex] = -7 $
(5.) WASSCE-FM Find the equation of the normal to the curve $y = 7x - 5x^2$ at
x = 2.
1st: We shall find the slope of the tangent to the curve at at x = 2.
This is the derivative of the function at x = 2.
2nd: We shall determine the slope of the normal to the curve
The normal to the curve is perpendicular to the tangent to the curve
Hence, the product of the two slopes (product of the slope of the tangent and the slope of the normal) is −1
3rd: We shall determine the point (x1, y1) on the curve
We already know the x-coordinate, but we shall find the y-coordinate
4th: We shall use the Point-Slope Form to determine the equation of the normal to the curve.
$ y = 7x - 5x^2 \\[3ex] \underline{\text{Slope of the tangent to the curve}}, m_T \\[3ex] \dfrac{dy}{dx} = 7 - 10x \\[3ex] @\;x = 2 \\[3ex] m_T = \left.\dfrac{dy}{dx}\right|_{x = 2} \\[5ex] = 7 - 10(2) \\[3ex] = 7 - 20 \\[3ex] = -13 \\[5ex] \underline{\text{Slope of the normal to the curve}}, m_N \\[3ex] m_N * m_T = -1 \\[3ex] m_N * 13 = -1 \\[3ex] m_N = \dfrac{-1}{-13} \\[5ex] m_N = \dfrac{1}{13} \\[5ex] \underline{\text{Point on the curve}}, (x_1, y_1) \\[3ex] y = 7x - 5x^2 \\[3ex] @\;x = 2 \\[3ex] y = 7(2) - 5(2)^2 \\[3ex] = 14 - 5(4) \\[3ex] = 14 - 20 \\[3ex] = -6 \\[3ex] (x_1, y_1) = (2, -6) \\[5ex] \underline{\text{Equation of the normal to the curve}} \\[3ex] \text{Point – Slope Form} \\[3ex] y - y_1 = m_N(x - x_1) \\[4ex] y - -6 = \dfrac{1}{13}(x - 2) \\[5ex] y + 6 = \dfrac{1}{13}x - \dfrac{2}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - 6 \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - \dfrac{78}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{80}{13} \\[5ex] LCD = 13 \\[3ex] \text{Multiply each term by 13} \\[3ex] 13y = 13\left(\dfrac{1}{13}x\right) - 13\left(\dfrac{80}{13}\right) \\[5ex] 13y = x - 80 \\[3ex] 13y - x + 80 = 0 $
1st: We shall find the slope of the tangent to the curve at at x = 2.
This is the derivative of the function at x = 2.
2nd: We shall determine the slope of the normal to the curve
The normal to the curve is perpendicular to the tangent to the curve
Hence, the product of the two slopes (product of the slope of the tangent and the slope of the normal) is −1
3rd: We shall determine the point (x1, y1) on the curve
We already know the x-coordinate, but we shall find the y-coordinate
4th: We shall use the Point-Slope Form to determine the equation of the normal to the curve.
$ y = 7x - 5x^2 \\[3ex] \underline{\text{Slope of the tangent to the curve}}, m_T \\[3ex] \dfrac{dy}{dx} = 7 - 10x \\[3ex] @\;x = 2 \\[3ex] m_T = \left.\dfrac{dy}{dx}\right|_{x = 2} \\[5ex] = 7 - 10(2) \\[3ex] = 7 - 20 \\[3ex] = -13 \\[5ex] \underline{\text{Slope of the normal to the curve}}, m_N \\[3ex] m_N * m_T = -1 \\[3ex] m_N * 13 = -1 \\[3ex] m_N = \dfrac{-1}{-13} \\[5ex] m_N = \dfrac{1}{13} \\[5ex] \underline{\text{Point on the curve}}, (x_1, y_1) \\[3ex] y = 7x - 5x^2 \\[3ex] @\;x = 2 \\[3ex] y = 7(2) - 5(2)^2 \\[3ex] = 14 - 5(4) \\[3ex] = 14 - 20 \\[3ex] = -6 \\[3ex] (x_1, y_1) = (2, -6) \\[5ex] \underline{\text{Equation of the normal to the curve}} \\[3ex] \text{Point – Slope Form} \\[3ex] y - y_1 = m_N(x - x_1) \\[4ex] y - -6 = \dfrac{1}{13}(x - 2) \\[5ex] y + 6 = \dfrac{1}{13}x - \dfrac{2}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - 6 \\[5ex] y = \dfrac{1}{13}x - \dfrac{2}{13} - \dfrac{78}{13} \\[5ex] y = \dfrac{1}{13}x - \dfrac{80}{13} \\[5ex] LCD = 13 \\[3ex] \text{Multiply each term by 13} \\[3ex] 13y = 13\left(\dfrac{1}{13}x\right) - 13\left(\dfrac{80}{13}\right) \\[5ex] 13y = x - 80 \\[3ex] 13y - x + 80 = 0 $
(6.) JAMB If $\dfrac{\pi}{2} \lt \theta \lt 2\pi$, find the maximum value of
$f(\theta) = \dfrac{4}{6 + 2\cos\theta}$
$ A.\:\: \dfrac{1}{2} \\[5ex] B.\:\: 4 \\[3ex] C.\:\: 1 \\[3ex] D.\:\: \dfrac{2}{3} \\[5ex] $
$ f(\theta) = \dfrac{4}{6 + 2\cos\theta} \\[5ex] u = 4 \\[3ex] \dfrac{du}{d\theta} = 0 \\[5ex] v = 6 + 2\cos\theta \\[3ex] \dfrac{dv}{d\theta} = 2 * -\sin\theta + \cos\theta * 0 = -2\sin\theta + 0 = -2\sin\theta \\[5ex] f'(\theta) = \dfrac{v\dfrac{du}{d\theta} - u\dfrac{du}{d\theta}}{v^2} \\[5ex] f'(\theta) = \dfrac{(6 + 2\cos\theta)(0) - 4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] f'(\theta) = \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] Set\:\:f'(\theta) = 0 \\[3ex] \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} = 0 \\[5ex] -4(-2\sin\theta) = 0((6 + 2\cos\theta)^2) \\[3ex] 8\sin\theta = 0 \\[3ex] \sin\theta = \dfrac{0}{8} \\[5ex] \sin\theta = 0 \\[3ex] \theta = 0, \pi, 2\pi ...Unit\:\:Circle\:\:Trigonometry \\[3ex] But\:\:\dfrac{\pi}{2} \lt \theta \lt 2\pi...Question \\[3ex] \therefore \theta = \pi = 180^\circ \\[3ex] Substitute\:\:for\:\:\theta\:\:in\:\:the\:\:main\:\:equation \\[3ex] f(\theta) = \dfrac{4}{6 + 2\cos180^\circ} \\[5ex] \cos180^\circ = -1 \\[3ex] f(\theta) = \dfrac{4}{6 + 2(-1)} \\[5ex] f(\theta) = \dfrac{4}{6 - 2} \\[5ex] f(\theta) = \dfrac{4}{4} \\[5ex] f(\theta) = 1 $
$ A.\:\: \dfrac{1}{2} \\[5ex] B.\:\: 4 \\[3ex] C.\:\: 1 \\[3ex] D.\:\: \dfrac{2}{3} \\[5ex] $
$ f(\theta) = \dfrac{4}{6 + 2\cos\theta} \\[5ex] u = 4 \\[3ex] \dfrac{du}{d\theta} = 0 \\[5ex] v = 6 + 2\cos\theta \\[3ex] \dfrac{dv}{d\theta} = 2 * -\sin\theta + \cos\theta * 0 = -2\sin\theta + 0 = -2\sin\theta \\[5ex] f'(\theta) = \dfrac{v\dfrac{du}{d\theta} - u\dfrac{du}{d\theta}}{v^2} \\[5ex] f'(\theta) = \dfrac{(6 + 2\cos\theta)(0) - 4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] f'(\theta) = \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} \\[5ex] Set\:\:f'(\theta) = 0 \\[3ex] \dfrac{-4(-2\sin\theta)}{(6 + 2\cos\theta)^2} = 0 \\[5ex] -4(-2\sin\theta) = 0((6 + 2\cos\theta)^2) \\[3ex] 8\sin\theta = 0 \\[3ex] \sin\theta = \dfrac{0}{8} \\[5ex] \sin\theta = 0 \\[3ex] \theta = 0, \pi, 2\pi ...Unit\:\:Circle\:\:Trigonometry \\[3ex] But\:\:\dfrac{\pi}{2} \lt \theta \lt 2\pi...Question \\[3ex] \therefore \theta = \pi = 180^\circ \\[3ex] Substitute\:\:for\:\:\theta\:\:in\:\:the\:\:main\:\:equation \\[3ex] f(\theta) = \dfrac{4}{6 + 2\cos180^\circ} \\[5ex] \cos180^\circ = -1 \\[3ex] f(\theta) = \dfrac{4}{6 + 2(-1)} \\[5ex] f(\theta) = \dfrac{4}{6 - 2} \\[5ex] f(\theta) = \dfrac{4}{4} \\[5ex] f(\theta) = 1 $
(7.) Consider a function $y = 3x^2 + 2x - 7$
(a.) Derive the gradient function $\dfrac{dy}{dx}$
(b.) Use it to find the local minimum or maximum point.
Assess whether it is a minimum or a maximum.
$ y = 3x^2 + 2x - 7 \\[3ex] f(x) = 3x^2 + 2x - 7 \\[3ex] (a.) \\[3ex] \dfrac{dy}{dx} = 6x + 2 \\[5ex] (b.) \\[3ex] \underline{\text{Second Derivative Test}} \\[3ex] \text{Critical Points: Set the derivative to zero and solve for }x \\[3ex] 6x + 2 = 0 \\[3ex] 6x = -2 \\[3ex] x = -\dfrac{2}{6} = -\dfrac{1}{3} \\[5ex] \text{Find the function value at the critical point} \\[3ex] f\left(-\dfrac{1}{3}\right) \\[5ex] = 3\left(-\dfrac{1}{3}\right)^2 + 2\left(-\dfrac{1}{3}\right) - 7 \\[5ex] = 3\left(-\dfrac{1}{9}\right) - \dfrac{2}{3} - \dfrac{21}{3} \\[5ex] = \dfrac{1}{3} - \dfrac{2}{3} - \dfrac{21}{3} \\[5ex] = \dfrac{1 - 2 - 21}{3} \\[5ex] = -\dfrac{22}{3} \\[5ex] \text{Point } \left(-\dfrac{1}{3}, -\dfrac{22}{3}\right) \text{ is a local maximum or a local minimum} \\[5ex] \text{To determine if the point is a local maximum or a local minimum:} \\[3ex] \text{Second Derivative: Find the derivative of the derivative} \\[3ex] \dfrac{d^2y}{dx^2} = 6 \\[5ex] 6 \gt 0 \\[3ex] \text{Hence, Point } \left(-\dfrac{1}{3}, -\dfrac{22}{3}\right) \text{ is a local minimum} \\[5ex] \text{To confirm if the point is a local maximum or a local minimum:} \\[3ex] \text{Critical Value, } x = -\dfrac{1}{3} \\[5ex] \text{Test Intervals are: } x \lt -\dfrac{1}{3} \hspace{1em}\text{and}\hspace{1em} x \gt -\dfrac{1}{3} \\[5ex] \text{First Derivative Test: Sign Test} \\[3ex] $
(a.) Derive the gradient function $\dfrac{dy}{dx}$
(b.) Use it to find the local minimum or maximum point.
Assess whether it is a minimum or a maximum.
$ y = 3x^2 + 2x - 7 \\[3ex] f(x) = 3x^2 + 2x - 7 \\[3ex] (a.) \\[3ex] \dfrac{dy}{dx} = 6x + 2 \\[5ex] (b.) \\[3ex] \underline{\text{Second Derivative Test}} \\[3ex] \text{Critical Points: Set the derivative to zero and solve for }x \\[3ex] 6x + 2 = 0 \\[3ex] 6x = -2 \\[3ex] x = -\dfrac{2}{6} = -\dfrac{1}{3} \\[5ex] \text{Find the function value at the critical point} \\[3ex] f\left(-\dfrac{1}{3}\right) \\[5ex] = 3\left(-\dfrac{1}{3}\right)^2 + 2\left(-\dfrac{1}{3}\right) - 7 \\[5ex] = 3\left(-\dfrac{1}{9}\right) - \dfrac{2}{3} - \dfrac{21}{3} \\[5ex] = \dfrac{1}{3} - \dfrac{2}{3} - \dfrac{21}{3} \\[5ex] = \dfrac{1 - 2 - 21}{3} \\[5ex] = -\dfrac{22}{3} \\[5ex] \text{Point } \left(-\dfrac{1}{3}, -\dfrac{22}{3}\right) \text{ is a local maximum or a local minimum} \\[5ex] \text{To determine if the point is a local maximum or a local minimum:} \\[3ex] \text{Second Derivative: Find the derivative of the derivative} \\[3ex] \dfrac{d^2y}{dx^2} = 6 \\[5ex] 6 \gt 0 \\[3ex] \text{Hence, Point } \left(-\dfrac{1}{3}, -\dfrac{22}{3}\right) \text{ is a local minimum} \\[5ex] \text{To confirm if the point is a local maximum or a local minimum:} \\[3ex] \text{Critical Value, } x = -\dfrac{1}{3} \\[5ex] \text{Test Intervals are: } x \lt -\dfrac{1}{3} \hspace{1em}\text{and}\hspace{1em} x \gt -\dfrac{1}{3} \\[5ex] \text{First Derivative Test: Sign Test} \\[3ex] $
|
$x \lt -\dfrac{1}{3}$ Let x = −1 |
$x \gt -\dfrac{1}{3}$ Let x = 0 |
|---|---|
| $ 6(-1) + 2 \\[3ex] -4 \\[3ex] $ | $ 6(0) + 2 \\[3ex] 2 \\[3ex] $ |
| negative | positive |
|
Because the slope changes from negative to positive, the function changes from decreasing to increasing. This implies that $x = -\dfrac{1}{3}$ is a local minimum. |
|
(8.)
(9.)
(10.) WASSCE-FM A curve is given by $y = 8x + \dfrac{27}{2x^2}$.
Find:
(a.) an expression for $\dfrac{dy}{dx}$;
(b.) the coordinates of the stationary point on the curve and the nature of the stationary point;
(c.) the equation of the normal to the curve at (2, 2)
$ (a.) \\[3ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] = 8x + \dfrac{27}{2} * \dfrac{1}{x^2} \\[5ex] = 8x^1 + \dfrac{27}{2} * x^{-2} \\[5ex] \dfrac{dy}{dx} = 1 * 8x^{1 - 1} + -2 * \dfrac{27}{2} * x^{-2 - 1} \\[5ex] = 8x^0 + -27x^{-3} \\[3ex] = 8(1) - \dfrac{27}{x^3} \\[5ex] = 8 - \dfrac{27}{x^3} \\[5ex] (b.) \\[3ex] \dfrac{dy}{dx} = 0 \\[5ex] 8 - \dfrac{27}{x^3} = 0 \\[5ex] 8 = \dfrac{27}{x^3} \\[5ex] 8x^3 = 27 \\[3ex] x^3 = \dfrac{27}{8} \\[5ex] x = \sqrt[3]{\dfrac{27}{8}} \\[5ex] x = \dfrac{3}{2} \\[5ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] y = 8x + 27 \div 2x^2 \\[5ex] @\; x = \dfrac{3}{2} \\[5ex] y = 8\left(\dfrac{3}{2}\right) + 27 \div 2\left(\dfrac{3}{2}\right)^2 \\[5ex] = 4(3) + 27 \div \dfrac{3^2}{2} \\[5ex] = 12 + 27 \div \dfrac{9}{2} \\[5ex] = 12 + 27 * \dfrac{2}{9} \\[5ex] = 12 + 6 \\[3ex] = 18 \\[3ex] \text{Stationary Point} = (x, y) = \left(\dfrac{3}{2}, 18\right) \\[5ex] $ To determine the nature of the stationary point, let us use the Second Derivative Test
If the second derivative is positive at the stationary point, the graph of the function is concave upward, and the point is a local minimum.
If the second derivative is negative, the graph of the function is concave downward, and the point is a local maximum.
$ \underline{\text{Nature of the Stationary Point: 2nd Derivative Test}} \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] \dfrac{dy}{dx} = 8 - 27x^{-3} \\[5ex] \dfrac{d^2y}{dx^2} = -3 * -27 * x^{-3 - 1} \\[5ex] = 81 * x^{-4} \\[3ex] = \dfrac{81}{x^4} \\[5ex] = 81 \div x^4 \\[3ex] @\; x = \dfrac{3}{2} \\[5ex] \dfrac{d^2y}{dx^2} = 81 \div \left(\dfrac{3}{2}\right)^4 \\[5ex] = 81 \div \dfrac{3^4}{2^4} \\[5ex] = 81 \div \dfrac{81}{16} \\[5ex] = 81 * \dfrac{16}{81} \\[5ex] = 16 \\[3ex] 16 \gt 0 \\[3ex] \therefore \left(\dfrac{3}{2}, 18\right) \text{is a minimum point} \\[5ex] $ Let:
m1 = slope of the tangent to the curve = derivative
m2 = slope of the normal to the curve
The product of the two slopes is −1 because the normal to the curve is perpendicular to the tangent to the curve
$ (c.) \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] @\; (2, 2) \\[3ex] m_1 = \left.\dfrac{dy}{dx}\right|_{x = 2} = 8 - \dfrac{27}{2^3} \\[5ex] = 8 - \dfrac{27}{8} \\[5ex] = \dfrac{64}{8} - \dfrac{27}{8} \\[5ex] = \dfrac{64 - 27}{8} \\[5ex] = \dfrac{37}{8} \\[5ex] m_1 * m_2 = -1 \\[3ex] m_2 = -\dfrac{1}{m_1} \\[5ex] = -1 \div m_1 \\[3ex] = -1 \div \dfrac{37}{8} \\[5ex] = -1 * \dfrac{8}{37} \\[5ex] = -\dfrac{8}{27} \\[5ex] For\;\;(2, 2) \\[3ex] (x_1, y_1) = (2, 2) \\[3ex] x_1 = 2 \\[3ex] y_1 = 2 \\[5ex] \underline{\text{Point — Slope Form}} \\[3ex] y - y_1 = m_2(x - x_1) \\[3ex] y - 2 = -\dfrac{8}{27}(x - 2) \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + 2 \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + \dfrac{74}{37} \\[5ex] y = \dfrac{-8x}{37} + \dfrac{90}{37} \\[5ex] LCD = 37 \\[3ex] 37y = 37\left(\dfrac{-8x}{37}\right) + 37\left(\dfrac{90}{37}\right) \\[5ex] 37y = -8x + 90 \\[3ex] 37y + 8x - 90 = 0 $
Find:
(a.) an expression for $\dfrac{dy}{dx}$;
(b.) the coordinates of the stationary point on the curve and the nature of the stationary point;
(c.) the equation of the normal to the curve at (2, 2)
$ (a.) \\[3ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] = 8x + \dfrac{27}{2} * \dfrac{1}{x^2} \\[5ex] = 8x^1 + \dfrac{27}{2} * x^{-2} \\[5ex] \dfrac{dy}{dx} = 1 * 8x^{1 - 1} + -2 * \dfrac{27}{2} * x^{-2 - 1} \\[5ex] = 8x^0 + -27x^{-3} \\[3ex] = 8(1) - \dfrac{27}{x^3} \\[5ex] = 8 - \dfrac{27}{x^3} \\[5ex] (b.) \\[3ex] \dfrac{dy}{dx} = 0 \\[5ex] 8 - \dfrac{27}{x^3} = 0 \\[5ex] 8 = \dfrac{27}{x^3} \\[5ex] 8x^3 = 27 \\[3ex] x^3 = \dfrac{27}{8} \\[5ex] x = \sqrt[3]{\dfrac{27}{8}} \\[5ex] x = \dfrac{3}{2} \\[5ex] y = 8x + \dfrac{27}{2x^2} \\[5ex] y = 8x + 27 \div 2x^2 \\[5ex] @\; x = \dfrac{3}{2} \\[5ex] y = 8\left(\dfrac{3}{2}\right) + 27 \div 2\left(\dfrac{3}{2}\right)^2 \\[5ex] = 4(3) + 27 \div \dfrac{3^2}{2} \\[5ex] = 12 + 27 \div \dfrac{9}{2} \\[5ex] = 12 + 27 * \dfrac{2}{9} \\[5ex] = 12 + 6 \\[3ex] = 18 \\[3ex] \text{Stationary Point} = (x, y) = \left(\dfrac{3}{2}, 18\right) \\[5ex] $ To determine the nature of the stationary point, let us use the Second Derivative Test
If the second derivative is positive at the stationary point, the graph of the function is concave upward, and the point is a local minimum.
If the second derivative is negative, the graph of the function is concave downward, and the point is a local maximum.
$ \underline{\text{Nature of the Stationary Point: 2nd Derivative Test}} \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] \dfrac{dy}{dx} = 8 - 27x^{-3} \\[5ex] \dfrac{d^2y}{dx^2} = -3 * -27 * x^{-3 - 1} \\[5ex] = 81 * x^{-4} \\[3ex] = \dfrac{81}{x^4} \\[5ex] = 81 \div x^4 \\[3ex] @\; x = \dfrac{3}{2} \\[5ex] \dfrac{d^2y}{dx^2} = 81 \div \left(\dfrac{3}{2}\right)^4 \\[5ex] = 81 \div \dfrac{3^4}{2^4} \\[5ex] = 81 \div \dfrac{81}{16} \\[5ex] = 81 * \dfrac{16}{81} \\[5ex] = 16 \\[3ex] 16 \gt 0 \\[3ex] \therefore \left(\dfrac{3}{2}, 18\right) \text{is a minimum point} \\[5ex] $ Let:
m1 = slope of the tangent to the curve = derivative
m2 = slope of the normal to the curve
The product of the two slopes is −1 because the normal to the curve is perpendicular to the tangent to the curve
$ (c.) \\[3ex] \dfrac{dy}{dx} = 8 - \dfrac{27}{x^3} \\[5ex] @\; (2, 2) \\[3ex] m_1 = \left.\dfrac{dy}{dx}\right|_{x = 2} = 8 - \dfrac{27}{2^3} \\[5ex] = 8 - \dfrac{27}{8} \\[5ex] = \dfrac{64}{8} - \dfrac{27}{8} \\[5ex] = \dfrac{64 - 27}{8} \\[5ex] = \dfrac{37}{8} \\[5ex] m_1 * m_2 = -1 \\[3ex] m_2 = -\dfrac{1}{m_1} \\[5ex] = -1 \div m_1 \\[3ex] = -1 \div \dfrac{37}{8} \\[5ex] = -1 * \dfrac{8}{37} \\[5ex] = -\dfrac{8}{27} \\[5ex] For\;\;(2, 2) \\[3ex] (x_1, y_1) = (2, 2) \\[3ex] x_1 = 2 \\[3ex] y_1 = 2 \\[5ex] \underline{\text{Point — Slope Form}} \\[3ex] y - y_1 = m_2(x - x_1) \\[3ex] y - 2 = -\dfrac{8}{27}(x - 2) \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + 2 \\[5ex] y = -\dfrac{8x}{37} + \dfrac{16}{37} + \dfrac{74}{37} \\[5ex] y = \dfrac{-8x}{37} + \dfrac{90}{37} \\[5ex] LCD = 37 \\[3ex] 37y = 37\left(\dfrac{-8x}{37}\right) + 37\left(\dfrac{90}{37}\right) \\[5ex] 37y = -8x + 90 \\[3ex] 37y + 8x - 90 = 0 $
(11.)
(12.)
(13.)
(14.)
(15.)
(16.)
(17.)
(18.) USSCE: Advance Mathematics Paper 1 The equation of the tangent to the curve
$y = (x^2 - 1)x$ at the point (1, 0) is
$ A.\;\; y = \dfrac{1}{4}x - \dfrac{9}{8} \\[5ex] B.\;\; y = \dfrac{1}{4}x + \dfrac{9}{8} \\[5ex] C.\;\; y = -\dfrac{1}{4}x + \dfrac{9}{8} \\[5ex] D.\;\; \text{None of the above} \\[3ex] $
$ y = (x^2 - 1)x \\[3ex] y = x(x^2 - 1) \\[3ex] y' = x(2x) + (x^2 - 1)(1)...\text{Product Rule} \\[3ex] y' = 2x^2 + x^2 - 1 \\[3ex] y' = 3x^2 - 1 \\[3ex] \text{At the point } (1, 0) \\[3ex] x = 1 \\[3ex] y = 0 \\[3ex] m = y' = 3(1)^2 - 1 \\[3ex] m = 3(1) - 1 \\[3ex] m = 3 - 1 \\[3ex] m = 2 \\[3ex] \text{Equation of the tangent to the curve} \\[3ex] y - y_1 = m(x - x_1)...\text{Point-Slope Form} \\[3ex] x_1 = 1 \\[3ex] y_1 = 0 \\[3ex] m = 2 \\[3ex] \implies \\[3ex] y - 0 = 2(x - 1) \\[3ex] y = 2(x - 1) \\[3ex] y = 2x - 2 \\[3ex] $ None of the above
$ A.\;\; y = \dfrac{1}{4}x - \dfrac{9}{8} \\[5ex] B.\;\; y = \dfrac{1}{4}x + \dfrac{9}{8} \\[5ex] C.\;\; y = -\dfrac{1}{4}x + \dfrac{9}{8} \\[5ex] D.\;\; \text{None of the above} \\[3ex] $
$ y = (x^2 - 1)x \\[3ex] y = x(x^2 - 1) \\[3ex] y' = x(2x) + (x^2 - 1)(1)...\text{Product Rule} \\[3ex] y' = 2x^2 + x^2 - 1 \\[3ex] y' = 3x^2 - 1 \\[3ex] \text{At the point } (1, 0) \\[3ex] x = 1 \\[3ex] y = 0 \\[3ex] m = y' = 3(1)^2 - 1 \\[3ex] m = 3(1) - 1 \\[3ex] m = 3 - 1 \\[3ex] m = 2 \\[3ex] \text{Equation of the tangent to the curve} \\[3ex] y - y_1 = m(x - x_1)...\text{Point-Slope Form} \\[3ex] x_1 = 1 \\[3ex] y_1 = 0 \\[3ex] m = 2 \\[3ex] \implies \\[3ex] y - 0 = 2(x - 1) \\[3ex] y = 2(x - 1) \\[3ex] y = 2x - 2 \\[3ex] $ None of the above
(19.) JAMB Determine the maximum value of $y = 3x^2 - x^3$
$ A.\:\: 2 \\[3ex] B.\:\: 4 \\[3ex] C.\:\: 6 \\[3ex] D.\:\: 0 \\[3ex] $
$ y = 3x^2 - x^3 \\[3ex] y' = 6x - 3x^2 \\[3ex] Set\:\:y = 0 \\[3ex] 6x - 3x^2 = 0 \\[3ex] 3x(2 - x) = 0 \\[3ex] 3x = 0 \:\:OR\:\: 2 - x = 0 \\[3ex] x = \dfrac{0}{3} \:\:OR\:\: 2 - 0 = x \\[5ex] x = 0 \:\:OR\:\: x = 2 \\[3ex] $ To find the maximum value of $y$ in this case (we have two values of $x$), we can solve it usint at least two approaches.
Use whichever way you prefer.
$ \text{First Approach: Second Derivative Test} \\[3ex] y' = 6x - 3x^2 \\[3ex] y'' = 6 - 6x = 6(1 - x) \\[3ex] For\:\:x = 0 \\[3ex] y'' = 6(1 - 0) = 6(1) = 6 \\[3ex] 6 \gt 0 \\[3ex] x = 0 \:\:gives\:\:minimum\:\:y-value \\[3ex] For\:\:x = 2 \\[3ex] y'' = 6(1 - 2) = 6(-1) = -6 \\[3ex] -6 \lt 0 \\[3ex] x = 2 \text{ gives maximum } y-value \\[3ex] \text{Substitute }x = 2 \text{ in the main equation} \\[3ex] y = 3(2)^2 - 2^3 \\[3ex] y = 3(4) - 8 \\[3ex] y = 12 - 8 \\[3ex] y = 4 \\[5ex] \text{Second Approach: Test Values} \\[3ex] For\:\:x = 0 \\[3ex] y = 3(0)^2 - 0^3 \\[3ex] y = 3(0) - 0 \\[3ex] y = 0 - 0 \\[3ex] y = 0 \\[3ex] For\:\:x = 2 \\[3ex] y = 3(2)^2 - 2^3 \\[3ex] y = 3(4) - 8 \\[3ex] y = 12 - 8 \\[3ex] y = 4 \\[5ex] 4 \gt 0 \\[3ex] \therefore y = 4 $
$ A.\:\: 2 \\[3ex] B.\:\: 4 \\[3ex] C.\:\: 6 \\[3ex] D.\:\: 0 \\[3ex] $
$ y = 3x^2 - x^3 \\[3ex] y' = 6x - 3x^2 \\[3ex] Set\:\:y = 0 \\[3ex] 6x - 3x^2 = 0 \\[3ex] 3x(2 - x) = 0 \\[3ex] 3x = 0 \:\:OR\:\: 2 - x = 0 \\[3ex] x = \dfrac{0}{3} \:\:OR\:\: 2 - 0 = x \\[5ex] x = 0 \:\:OR\:\: x = 2 \\[3ex] $ To find the maximum value of $y$ in this case (we have two values of $x$), we can solve it usint at least two approaches.
Use whichever way you prefer.
$ \text{First Approach: Second Derivative Test} \\[3ex] y' = 6x - 3x^2 \\[3ex] y'' = 6 - 6x = 6(1 - x) \\[3ex] For\:\:x = 0 \\[3ex] y'' = 6(1 - 0) = 6(1) = 6 \\[3ex] 6 \gt 0 \\[3ex] x = 0 \:\:gives\:\:minimum\:\:y-value \\[3ex] For\:\:x = 2 \\[3ex] y'' = 6(1 - 2) = 6(-1) = -6 \\[3ex] -6 \lt 0 \\[3ex] x = 2 \text{ gives maximum } y-value \\[3ex] \text{Substitute }x = 2 \text{ in the main equation} \\[3ex] y = 3(2)^2 - 2^3 \\[3ex] y = 3(4) - 8 \\[3ex] y = 12 - 8 \\[3ex] y = 4 \\[5ex] \text{Second Approach: Test Values} \\[3ex] For\:\:x = 0 \\[3ex] y = 3(0)^2 - 0^3 \\[3ex] y = 3(0) - 0 \\[3ex] y = 0 - 0 \\[3ex] y = 0 \\[3ex] For\:\:x = 2 \\[3ex] y = 3(2)^2 - 2^3 \\[3ex] y = 3(4) - 8 \\[3ex] y = 12 - 8 \\[3ex] y = 4 \\[5ex] 4 \gt 0 \\[3ex] \therefore y = 4 $
(20.) Use Newton's method to determine the second and third approximations of the equation $2\sin x
= x$ as follows.
Let $x_1 = 2$ be the initial approximation.
$ 2\sin x = x \\[3ex] 2\sin x - x = 0 \\[3ex] 2\sin x - x = f(x) \\[3ex] f(x) = 2\sin x - x \\[3ex] f'(x) = 2\cos x - 1 \\[3ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = x_n - \dfrac{2\sin x_n - x_n}{2\cos x_n - 1} \\[5ex] $
$ x_2 = 1.900995594 \\[3ex] x_3 = 1.895511645 $
Let $x_1 = 2$ be the initial approximation.
$ 2\sin x = x \\[3ex] 2\sin x - x = 0 \\[3ex] 2\sin x - x = f(x) \\[3ex] f(x) = 2\sin x - x \\[3ex] f'(x) = 2\cos x - 1 \\[3ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = x_n - \dfrac{2\sin x_n - x_n}{2\cos x_n - 1} \\[5ex] $
| $n$ | $1$ | $2$ |
| $x_n$ | $2$ | $1.900995594$ |
| $\sin x_n$ | $0.9092974268$ | $0.9459777535$ |
| $2\sin x_n$ | $1.818594854$ | $1.891955507$ |
| $\color{purple}{2\sin x_n - x_n}$ | $-0.1814051463$ | $-0.009040087$ |
| $\cos x_n$ | $-0.4161468365$ | $-0.3242315372$ |
| $2\cos x_n$ | $-0.8322936731$ | $-0.6484630743$ |
| $\color{purple}{2\cos x_n - 1}$ | $-1.832293673$ | $-1.648463074$ |
| $\dfrac{2\sin x_n - x_n}{2\cos x_n - 1}$ | $0.0990044058$ | $0.0054839487$ |
| $\color{darkblue}{x_n - \dfrac{2\sin x_n - x_n}{2\cos x_n - 1}}$ | $\color{darkblue}{1.900995594}$ | $\color{darkblue}{1.895511645}$ |
$ x_2 = 1.900995594 \\[3ex] x_3 = 1.895511645 $
(21.) CSEC-AM (a.) (i.) Use the definition of the derivative as a limit to find
$f'(x)$ for the function $f(x) = x^2 - 3$
(ii.) Hence, determine the value of $f''(5)$
(b.) Given that $y = \dfrac{\sin x}{\cos x}$, show that $\dfrac{dy}{dx} = \dfrac{1}{\cos^2 x}$
(c.) The equation of a curve is given by $y = (5x^2 - 7)^4$
Determine the equation of the gradient of the curve.
$ (a.) (i.) \\[3ex] \underline{\text{Derivative by Limits}} \\[3ex] f(x) = x^2 - 3 \\[4ex] f(x + h) = (x + h)^2 - 3 \\[4ex] = (x + h)(x + h) - 3 \\[3ex] = x^2 + xh + xh + h^2 - 3 \\[4ex] = x^2 + 2xh + h^2 - 3 \\[5ex] f(x + h) - f(x) = x^2 + 2xh + h^2 - 3 - (x^2 - 3) \\[4ex] = x^2 + 2xh + h^2 - 3 - x^2 + 3 \\[4ex] = 2xh + h^2 \\[4ex] = h(2x + h) \\[5ex] \dfrac{f(x + h) - f(x)}{h} = \dfrac{h(2x + h)}{h} \\[5ex] = 2x + h \\[5ex] f'(x) = \displaystyle{\lim_{h \to 0}}\:\:2x + h \\[4ex] f'(x) = 2x + 0 \\[3ex] f'(x) = 2x \\[5ex] (ii.) \\[3ex] \underline{\text{Derivative by Rules}} \\[3ex] f'(x) = 2x \\[3ex] f''(x) = 2 \\[3ex] f''(5) = 2 \\[5ex] (b.) \\[3ex] y = \dfrac{\sin x}{\cos x} \\[5ex] \underline{\text{Quotient Rule}} \\[3ex] u = \sin x \hspace{4em} v = \cos x \\[3ex] u' = \cos x \hspace{4em} v' = -\sin x \\[5ex] \dfrac{dy}{dx} = \dfrac{vu' - uv'}{v^2} \\[6ex] = \dfrac{\cos x(\cos x) - \sin x(-\sin x)}{\cos^2 x} \\[6ex] = \dfrac{\cos^2 x + \sin^2 x}{\cos^2 x} \\[5ex] \cos^2 x + \sin^2 x = 1 ...\text{Pythagorean Identity} \\[4ex] = \dfrac{1}{\cos^2 x} \\[6ex] $ The equation of the gradient of the curve is the derivative of the curve
$ (c.) \\[3ex] y = (5x^2 - 7)^4 \\[4ex] \underline{\text{Chain Rule}} \\[3ex] Let\;\;p = 5x^2 - 7 \hspace{4em} y = p^4 \\[4ex] \dfrac{dp}{dx} = 10x \hspace{5em} \dfrac{dy}{dp} = 4p^3 \\[6ex] \dfrac{dy}{dx} = \dfrac{dy}{dp} * \dfrac{dp}{dx} \\[5ex] = 4p^3 * 10x \\[4ex] = 40xp^3 \\[4ex] = 40x(5x^2 - 7)^3 $
(ii.) Hence, determine the value of $f''(5)$
(b.) Given that $y = \dfrac{\sin x}{\cos x}$, show that $\dfrac{dy}{dx} = \dfrac{1}{\cos^2 x}$
(c.) The equation of a curve is given by $y = (5x^2 - 7)^4$
Determine the equation of the gradient of the curve.
$ (a.) (i.) \\[3ex] \underline{\text{Derivative by Limits}} \\[3ex] f(x) = x^2 - 3 \\[4ex] f(x + h) = (x + h)^2 - 3 \\[4ex] = (x + h)(x + h) - 3 \\[3ex] = x^2 + xh + xh + h^2 - 3 \\[4ex] = x^2 + 2xh + h^2 - 3 \\[5ex] f(x + h) - f(x) = x^2 + 2xh + h^2 - 3 - (x^2 - 3) \\[4ex] = x^2 + 2xh + h^2 - 3 - x^2 + 3 \\[4ex] = 2xh + h^2 \\[4ex] = h(2x + h) \\[5ex] \dfrac{f(x + h) - f(x)}{h} = \dfrac{h(2x + h)}{h} \\[5ex] = 2x + h \\[5ex] f'(x) = \displaystyle{\lim_{h \to 0}}\:\:2x + h \\[4ex] f'(x) = 2x + 0 \\[3ex] f'(x) = 2x \\[5ex] (ii.) \\[3ex] \underline{\text{Derivative by Rules}} \\[3ex] f'(x) = 2x \\[3ex] f''(x) = 2 \\[3ex] f''(5) = 2 \\[5ex] (b.) \\[3ex] y = \dfrac{\sin x}{\cos x} \\[5ex] \underline{\text{Quotient Rule}} \\[3ex] u = \sin x \hspace{4em} v = \cos x \\[3ex] u' = \cos x \hspace{4em} v' = -\sin x \\[5ex] \dfrac{dy}{dx} = \dfrac{vu' - uv'}{v^2} \\[6ex] = \dfrac{\cos x(\cos x) - \sin x(-\sin x)}{\cos^2 x} \\[6ex] = \dfrac{\cos^2 x + \sin^2 x}{\cos^2 x} \\[5ex] \cos^2 x + \sin^2 x = 1 ...\text{Pythagorean Identity} \\[4ex] = \dfrac{1}{\cos^2 x} \\[6ex] $ The equation of the gradient of the curve is the derivative of the curve
$ (c.) \\[3ex] y = (5x^2 - 7)^4 \\[4ex] \underline{\text{Chain Rule}} \\[3ex] Let\;\;p = 5x^2 - 7 \hspace{4em} y = p^4 \\[4ex] \dfrac{dp}{dx} = 10x \hspace{5em} \dfrac{dy}{dp} = 4p^3 \\[6ex] \dfrac{dy}{dx} = \dfrac{dy}{dp} * \dfrac{dp}{dx} \\[5ex] = 4p^3 * 10x \\[4ex] = 40xp^3 \\[4ex] = 40x(5x^2 - 7)^3 $
(22.) USSCE: Advance Mathematics Paper 1 The two stationary points on the curve $y =
\dfrac{2x}{x^2 + 1}$ are
$ A.\;\; (1, -1)\;\;and\;\;(-1, 1) \\[3ex] B.\;\; (-1, 1)\;\;and\;\;(1, 1) \\[3ex] C.\;\; (1, 1)\;\;and\;\;(-1, 1) \\[3ex] D.\;\; \text{None of the above} \\[3ex] $
$ y = \dfrac{2x}{x^2 + 1} = \dfrac{p}{k} \\[5ex] p = 2x \\[3ex] p' = 2 \\[3ex] k = x^2 + 1 \\[3ex] k' = 2x \\[3ex] y' = \dfrac{kp' - pk'}{k^2} \\[5ex] y' = \dfrac{(x^2 + 1)(2) - 2x(2x)}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2x^2 + 2 - 4x^2}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2 - 2x^2}{(x^2 + 1)^2} \\[5ex] \text{Stationary Points} \\[3ex] y' = 0 \\[3ex] \implies \\[3ex] \dfrac{2 - 2x^2}{(x^2 + 1)^2} = 0 \\[5ex] 2 - 2x^2 = 0 \\[3ex] 2 = 2x^2 \\[3ex] 2x^2 = 2 \\[3ex] x^2 = \dfrac{2}{2} \\[5ex] x^2 = 1 \\[3ex] x = \pm \sqrt{1} \\[3ex] x = \pm 1 \\[3ex] y = \dfrac{2x}{x^2 + 1} \\[5ex] when\;\; x = 1 \\[3ex] y = \dfrac{2(1)}{1^2 + 1} \\[5ex] y = \dfrac{2}{1 + 1} \\[5ex] y = \dfrac{2}{2} \\[5ex] y = 1 \\[3ex] (x, y) \rightarrow (1, 1) \\[3ex] when\;\; x = -1 \\[3ex] y = \dfrac{2(-1)}{(-1)^2 + 1} \\[5ex] y = \dfrac{-2}{1 + 1} \\[5ex] y = \dfrac{-2}{2} \\[5ex] y = -1 \\[3ex] (x, y) \rightarrow (-1, -1) \\[3ex] $ The stationary points are: (1, 1) and (−1, −1)
$ A.\;\; (1, -1)\;\;and\;\;(-1, 1) \\[3ex] B.\;\; (-1, 1)\;\;and\;\;(1, 1) \\[3ex] C.\;\; (1, 1)\;\;and\;\;(-1, 1) \\[3ex] D.\;\; \text{None of the above} \\[3ex] $
$ y = \dfrac{2x}{x^2 + 1} = \dfrac{p}{k} \\[5ex] p = 2x \\[3ex] p' = 2 \\[3ex] k = x^2 + 1 \\[3ex] k' = 2x \\[3ex] y' = \dfrac{kp' - pk'}{k^2} \\[5ex] y' = \dfrac{(x^2 + 1)(2) - 2x(2x)}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2x^2 + 2 - 4x^2}{(x^2 + 1)^2} \\[5ex] y' = \dfrac{2 - 2x^2}{(x^2 + 1)^2} \\[5ex] \text{Stationary Points} \\[3ex] y' = 0 \\[3ex] \implies \\[3ex] \dfrac{2 - 2x^2}{(x^2 + 1)^2} = 0 \\[5ex] 2 - 2x^2 = 0 \\[3ex] 2 = 2x^2 \\[3ex] 2x^2 = 2 \\[3ex] x^2 = \dfrac{2}{2} \\[5ex] x^2 = 1 \\[3ex] x = \pm \sqrt{1} \\[3ex] x = \pm 1 \\[3ex] y = \dfrac{2x}{x^2 + 1} \\[5ex] when\;\; x = 1 \\[3ex] y = \dfrac{2(1)}{1^2 + 1} \\[5ex] y = \dfrac{2}{1 + 1} \\[5ex] y = \dfrac{2}{2} \\[5ex] y = 1 \\[3ex] (x, y) \rightarrow (1, 1) \\[3ex] when\;\; x = -1 \\[3ex] y = \dfrac{2(-1)}{(-1)^2 + 1} \\[5ex] y = \dfrac{-2}{1 + 1} \\[5ex] y = \dfrac{-2}{2} \\[5ex] y = -1 \\[3ex] (x, y) \rightarrow (-1, -1) \\[3ex] $ The stationary points are: (1, 1) and (−1, −1)
(23.)
(24.)
(25.) NSC The graph of $h(x) = ax^3 + bx^2$ is drawn.
The graph has turning points at the origin, O(0 ; 0) and B(4 ; 32)
A is an x-intercept of h
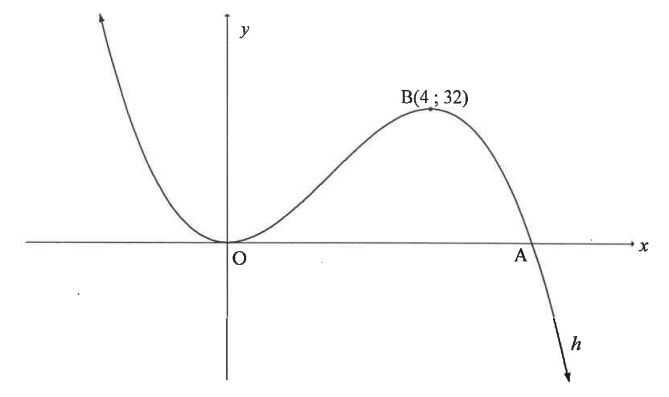
(25.1) Show that a = −1 and b = 6
(25.2) Calculate the coordinates of A
(25.3) Write down the values of x for which h is:
(25.3.1) Increasing
(25.3.2) Concave down
(25.4) For which values of k will $-(x - 1)^3 + 6(x - 1)^2 - k = 0$ have one negative and two distinct positive roots?
$ (25.1) \\[3ex] Function:\;\;h(x) = ax^3 + bx^2 \\[3ex] For\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] y = h(x) = 32 \\[3ex] \implies \\[3ex] 32 = a(4)^3 + b(4)^2 \\[3ex] 32 = 64a + 16b \\[3ex] 64a + 16b = 32 \\[3ex] \implies \\[3ex] 4a + b = 2 ...eqn.(1) \\[3ex] Also: \\[3ex] h(x) = ax^3 + bx^2 \\[3ex] h'(x) = 3ax^2 + 2bx \\[3ex] At\;\;turning\;\;point,\;\;h'(x) = 0 \\[3ex] For\;\;Turning\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] \implies \\[3ex] h'(4) = 0 \\[3ex] h'(4) = 3a(4)^2 + 2b(4) = 0 \\[3ex] 48a + 8b = 0 \\[3ex] \implies \\[3ex] 6a + b = 0 ...eqn.(2) \\[3ex] eqn.(2) - eqn.(1) \\[3ex] 6a - 4a = 0 - 2 \\[3ex] 2a = -2 \\[3ex] a = -\dfrac{2}{2} \\[5ex] a = -1 \\[3ex] Substitute\;\;a = -1 \;\;into\;\;eqn.(1) \\[3ex] 4(-1) + b = 2 \\[3ex] -4 + b = 2 \\[3ex] b = 2 + 4 \\[3ex] b = 6 \\[3ex] \therefore h(x) = -x^3 + 6x^2 \\[3ex] (25.2) \\[3ex] A = x-intercept\;\;of\;\;h(x) \\[3ex] \implies \\[3ex] h(x) = 0 \\[3ex] -x^3 + 6x^2 = 0 \\[3ex] x^2(-x + 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; -x + 6 = 0 \\[3ex] x = \pm \sqrt{0} \;\;\;OR\;\;\; 6 = 0 + x \\[3ex] x = \pm 0 \;\;\;OR\;\;\; 6 = x \\[3ex] Based\;\;on\;\;the\;\;graph:\;\; x \ne \pm 0 \\[3ex] x = 6 \\[3ex] \therefore coordinates\;\;of\;\;A = (6, 0) \\[3ex] (25.3) \\[3ex] (25.3.1) \\[3ex] Based\;\;on\;\;the\;\;Graph \\[3ex] h(x)\uparrow for\;\; x \in (0, 4) \\[3ex] (25.3.2) \\[3ex] Based\;\;on\;\;the\;\;function \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h'(x) = -3x^2 + 12x \\[3ex] h''(x) = -6x + 12 \\[3ex] h''(x) = 0 \\[3ex] \implies \\[3ex] -6x + 12 = 0 \\[3ex] -6x = -12 \\[3ex] x = \dfrac{-12}{-6} \\[5ex] Inflection\;\;Point:\;\;x = 2 \\[3ex] Intervals:\;\; x \lt 2 \;\;and\;\; x \gt 2 \\[3ex] $
$ h(x)\frown for\;\; x \gt 2 \\[3ex] h(x)\frown for\;\; x \in (2, \infty) \\[3ex] (25.4) \\[3ex] -(x - 1)^3 + 6(x - 1)^2 - k = 0 \\[3ex] -(x - 1)^3 + 6(x - 1)^2 = k \\[3ex] k = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] \implies k = h(x - 1) \\[3ex] k = graph\;\;of\;\;h(x - 1) \\[3ex] 1st\;\;find\;\;the\;\;y-intercept...value\;\;of\;\;k\;\;when\;\;x = 0 \\[3ex] k = -(0 - 1)^3 + 6(0 - 1)^2 \\[3ex] k = -(-1)^3 + 6(-1)^2 \\[3ex] k = -(-1) + 6(1) \\[3ex] k = 1 + 6 \\[3ex] k = 7 \\[3ex] Negative\;\;root \implies x \lt 0 \\[3ex] When\;\;x \lt 0,\;\;k \lt 7 \\[3ex] Let\;\;us\;\;find\;\;the\;\;maximum\;\;value\;\;for\;\;the\;\;positive\;\;roots \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x - 1)' = -3(x - 1)^2 + 12(x - 1) \\[3ex] h(x - 1)' = 0 \\[3ex] \implies \\[3ex] -3(x - 1)^2 + 12(x - 1) = 0 \\[3ex] -3(x^2 - 2x + 1) + 12x - 12 = 0 \\[3ex] -3x^2 + 6x - 3 + 12x - 12 = 0 \\[3ex] -3x^2 + 18x - 15 = 0 \\[3ex] x^2 - 6x + 5 = 0 \\[3ex] (x - 5)(x - 1) = 0 \\[3ex] x - 5 = 0 \;\;\;OR\;\;\; x - 1 = 0 \\[3ex] x = 5 \;\;\;OR\;\;\; x = 1 \\[3ex] For\;\;x = 5 \\[3ex] h(x - 1) = -(5 - 1)^3 + 6(5 - 1)^2 \\[3ex] = -4^3 + 6(4^2) \\[3ex] = -64 + 6(16) \\[3ex] = -64 + 96 \\[3ex] = 32 \\[3ex] For\;\;x = 1 \\[3ex] h(x - 1) = -(1 - 1)^3 + 6(0 - 1)^2 \\[3ex] = -0^3 + 6(-1)^2 \\[3ex] = 0 + 6(1) \\[3ex] = 0 + 6 \\[3ex] = 6 \\[3ex] Maximum\;\;value = 32 \\[3ex] \implies \\[3ex] 7 \lt k \lt 32 $
The graph has turning points at the origin, O(0 ; 0) and B(4 ; 32)
A is an x-intercept of h

(25.1) Show that a = −1 and b = 6
(25.2) Calculate the coordinates of A
(25.3) Write down the values of x for which h is:
(25.3.1) Increasing
(25.3.2) Concave down
(25.4) For which values of k will $-(x - 1)^3 + 6(x - 1)^2 - k = 0$ have one negative and two distinct positive roots?
$ (25.1) \\[3ex] Function:\;\;h(x) = ax^3 + bx^2 \\[3ex] For\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] y = h(x) = 32 \\[3ex] \implies \\[3ex] 32 = a(4)^3 + b(4)^2 \\[3ex] 32 = 64a + 16b \\[3ex] 64a + 16b = 32 \\[3ex] \implies \\[3ex] 4a + b = 2 ...eqn.(1) \\[3ex] Also: \\[3ex] h(x) = ax^3 + bx^2 \\[3ex] h'(x) = 3ax^2 + 2bx \\[3ex] At\;\;turning\;\;point,\;\;h'(x) = 0 \\[3ex] For\;\;Turning\;\;Point\;B(4, 32) \\[3ex] x = 4 \\[3ex] \implies \\[3ex] h'(4) = 0 \\[3ex] h'(4) = 3a(4)^2 + 2b(4) = 0 \\[3ex] 48a + 8b = 0 \\[3ex] \implies \\[3ex] 6a + b = 0 ...eqn.(2) \\[3ex] eqn.(2) - eqn.(1) \\[3ex] 6a - 4a = 0 - 2 \\[3ex] 2a = -2 \\[3ex] a = -\dfrac{2}{2} \\[5ex] a = -1 \\[3ex] Substitute\;\;a = -1 \;\;into\;\;eqn.(1) \\[3ex] 4(-1) + b = 2 \\[3ex] -4 + b = 2 \\[3ex] b = 2 + 4 \\[3ex] b = 6 \\[3ex] \therefore h(x) = -x^3 + 6x^2 \\[3ex] (25.2) \\[3ex] A = x-intercept\;\;of\;\;h(x) \\[3ex] \implies \\[3ex] h(x) = 0 \\[3ex] -x^3 + 6x^2 = 0 \\[3ex] x^2(-x + 6) = 0 \\[3ex] x^2 = 0 \;\;\;OR\;\;\; -x + 6 = 0 \\[3ex] x = \pm \sqrt{0} \;\;\;OR\;\;\; 6 = 0 + x \\[3ex] x = \pm 0 \;\;\;OR\;\;\; 6 = x \\[3ex] Based\;\;on\;\;the\;\;graph:\;\; x \ne \pm 0 \\[3ex] x = 6 \\[3ex] \therefore coordinates\;\;of\;\;A = (6, 0) \\[3ex] (25.3) \\[3ex] (25.3.1) \\[3ex] Based\;\;on\;\;the\;\;Graph \\[3ex] h(x)\uparrow for\;\; x \in (0, 4) \\[3ex] (25.3.2) \\[3ex] Based\;\;on\;\;the\;\;function \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h'(x) = -3x^2 + 12x \\[3ex] h''(x) = -6x + 12 \\[3ex] h''(x) = 0 \\[3ex] \implies \\[3ex] -6x + 12 = 0 \\[3ex] -6x = -12 \\[3ex] x = \dfrac{-12}{-6} \\[5ex] Inflection\;\;Point:\;\;x = 2 \\[3ex] Intervals:\;\; x \lt 2 \;\;and\;\; x \gt 2 \\[3ex] $
| Interval | $x \lt 2$ | $x \gt 2$ |
| Test Value | $x = 1$ | $x = 3$ |
| Sign Test | $$ -6(1) + 12 \\[3ex] -6 + 12 = 6 \\[3ex] 6 \gt 0 \\[3ex] positive $$ | $$ -6(3) + 12 \\[3ex] -18 + 12 = -6 \\[3ex] -6 \lt 0 \\[3ex] negative $$ |
| Conclusion | Concave up | Concave down |
$ h(x)\frown for\;\; x \gt 2 \\[3ex] h(x)\frown for\;\; x \in (2, \infty) \\[3ex] (25.4) \\[3ex] -(x - 1)^3 + 6(x - 1)^2 - k = 0 \\[3ex] -(x - 1)^3 + 6(x - 1)^2 = k \\[3ex] k = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x) = -x^3 + 6x^2 \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] \implies k = h(x - 1) \\[3ex] k = graph\;\;of\;\;h(x - 1) \\[3ex] 1st\;\;find\;\;the\;\;y-intercept...value\;\;of\;\;k\;\;when\;\;x = 0 \\[3ex] k = -(0 - 1)^3 + 6(0 - 1)^2 \\[3ex] k = -(-1)^3 + 6(-1)^2 \\[3ex] k = -(-1) + 6(1) \\[3ex] k = 1 + 6 \\[3ex] k = 7 \\[3ex] Negative\;\;root \implies x \lt 0 \\[3ex] When\;\;x \lt 0,\;\;k \lt 7 \\[3ex] Let\;\;us\;\;find\;\;the\;\;maximum\;\;value\;\;for\;\;the\;\;positive\;\;roots \\[3ex] h(x - 1) = -(x - 1)^3 + 6(x - 1)^2 \\[3ex] h(x - 1)' = -3(x - 1)^2 + 12(x - 1) \\[3ex] h(x - 1)' = 0 \\[3ex] \implies \\[3ex] -3(x - 1)^2 + 12(x - 1) = 0 \\[3ex] -3(x^2 - 2x + 1) + 12x - 12 = 0 \\[3ex] -3x^2 + 6x - 3 + 12x - 12 = 0 \\[3ex] -3x^2 + 18x - 15 = 0 \\[3ex] x^2 - 6x + 5 = 0 \\[3ex] (x - 5)(x - 1) = 0 \\[3ex] x - 5 = 0 \;\;\;OR\;\;\; x - 1 = 0 \\[3ex] x = 5 \;\;\;OR\;\;\; x = 1 \\[3ex] For\;\;x = 5 \\[3ex] h(x - 1) = -(5 - 1)^3 + 6(5 - 1)^2 \\[3ex] = -4^3 + 6(4^2) \\[3ex] = -64 + 6(16) \\[3ex] = -64 + 96 \\[3ex] = 32 \\[3ex] For\;\;x = 1 \\[3ex] h(x - 1) = -(1 - 1)^3 + 6(0 - 1)^2 \\[3ex] = -0^3 + 6(-1)^2 \\[3ex] = 0 + 6(1) \\[3ex] = 0 + 6 \\[3ex] = 6 \\[3ex] Maximum\;\;value = 32 \\[3ex] \implies \\[3ex] 7 \lt k \lt 32 $
(26.)
(27.)
(28.)
(29.) The function: $f(x) = \dfrac{7}{x} - 7\ln(x)$ has a root on [1, 2]
(a.) Choosing $x_1 = 1$, determine the exact value of the third approximation, $x_3$ for the root via Newton's method.
(b.) Then, continue to find the root, correct to 5 decimal places, for comparison.
$ (a.) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = 7x^{-1} - 7\ln x \\[3ex] f'(x) = -7x^-2 - \left[7\left(\dfrac{1}{x}\right) + \ln x(0)\right] \\[5ex] f'(x) = -7x^{-2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] Simplify\;\;f(x)\;\;and\;\;f'(x) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = \dfrac{7 - 7x\ln x}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7 - 7x}{x^2} \\[5ex] \dfrac{f(x)}{f'(x)} \\[5ex] = f(x) \div f'(x) \\[3ex] = \dfrac{7 - 7x\ln x}{x} \div \dfrac{-7 - 7x}{x^2} \\[5ex] = \dfrac{7 - 7x\ln x}{x} * \dfrac{x^2}{-7 - 7x} \\[5ex] = \dfrac{7(1 - x\ln x)}{x} * \dfrac{x^2}{-7(1 + x)} \\[5ex] = \dfrac{x(1 - x\ln x)}{-(1 + x)} \\[5ex] = \dfrac{x - x^2\ln x}{-(1 + x)} \\[5ex] = -\dfrac{(x - x^2\ln x)}{1 + x} \\[5ex] = \dfrac{-x + x^2\ln x}{x + 1} \\[5ex] = \dfrac{x^2\ln x - x}{x + 1} \\[5ex] x - \dfrac{f(x)}{f'(x)} \\[5ex] = x - \dfrac{x^2\ln x - x}{x + 1} \\[5ex] = \dfrac{x(x + 1) - (x^2\ln x - x)}{x + 1} \\[5ex] = \dfrac{x^2 + x - x^2\ln x + x}{x + 1} \\[5ex] = \dfrac{x^2 + 2x - x^2\ln x}{x + 1} \\[5ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = \dfrac{x_n^2 + 2x_n - x_n^2\ln x_n}{x_n + 1} \\[5ex] x_1 = 1 \\[3ex] \implies \\[3ex] x_2 = \dfrac{x_1^2 + 2x_1 - x_1^2\ln x_1}{x_1 + 1} \\[5ex] x_2 = \dfrac{1^2 + 2(1) - 1^2 * \ln(1)}{1 + 1} \\[5ex] x_2 = \dfrac{1 + 2 - 1 * 0}{2} \\[5ex] x_2 = \dfrac{1 + 2 - 0}{2} \\[5ex] x_2 = \dfrac{3}{2} \\[7ex] x_3 = \dfrac{x_2^2 + 2x_2 - x_2^2\ln x_2}{x_2 + 1} \\[5ex] \underline{Numerator} \\[3ex] x_2^2 + 2x_2 - x_2^2\ln x_2 \\[3ex] = \left(\dfrac{3}{2}\right)^2 + 2 * \dfrac{3}{2} - \left(\dfrac{3}{2}\right)^2 * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{9}{4} + 3 - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] \underline{Denominator} \\[3ex] x_2 + 1 \\[3ex] = \dfrac{3}{2} + 1 \\[5ex] = \dfrac{3 + 2}{2} \\[5ex] = \dfrac{5}{2} \\[5ex] Numerator \div Denominator \\[3ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \div \dfrac{5}{2} \\[5ex] = \dfrac{1}{4}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] * \dfrac{2}{5} \\[5ex] = \dfrac{1}{10}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] \\[5ex] = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] \therefore x_3 = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] (b.) \\[3ex] x_3 = 2.1 - (0.9 * \ln(1.5)) \\[3ex] x_3 = 1.735081403 \\[3ex] $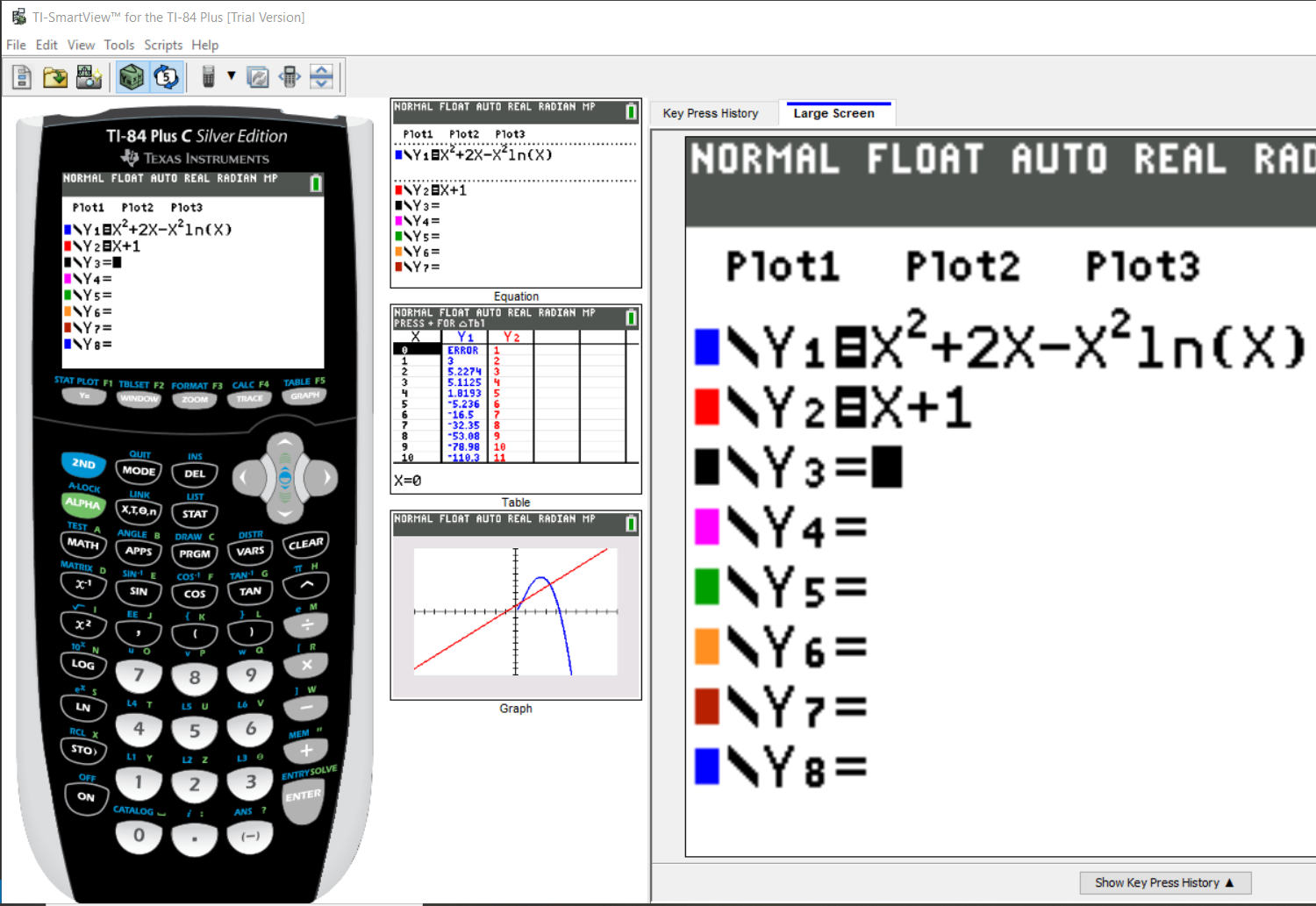
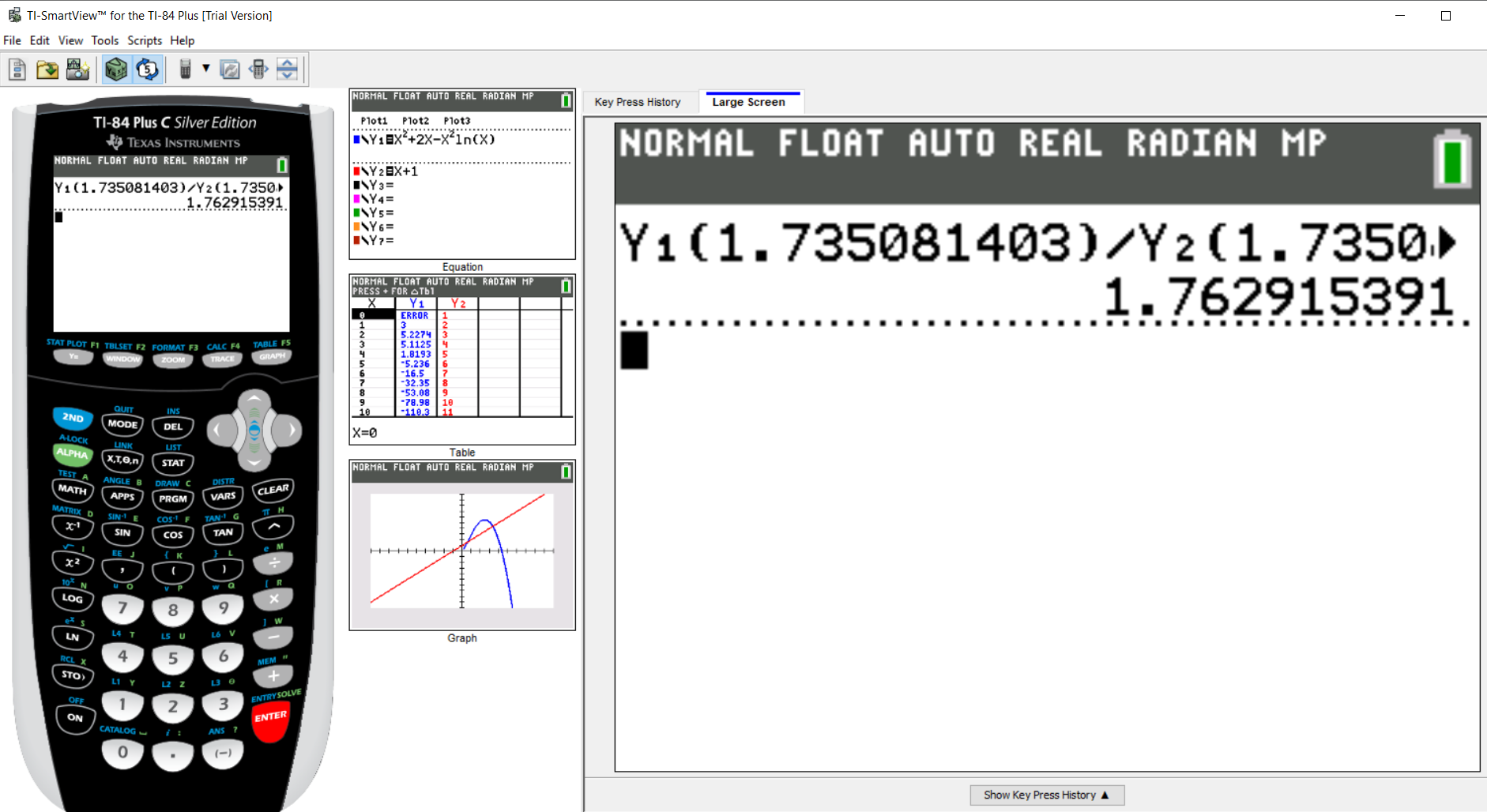
$ x_4 = 1.762915391 \\[3ex] $
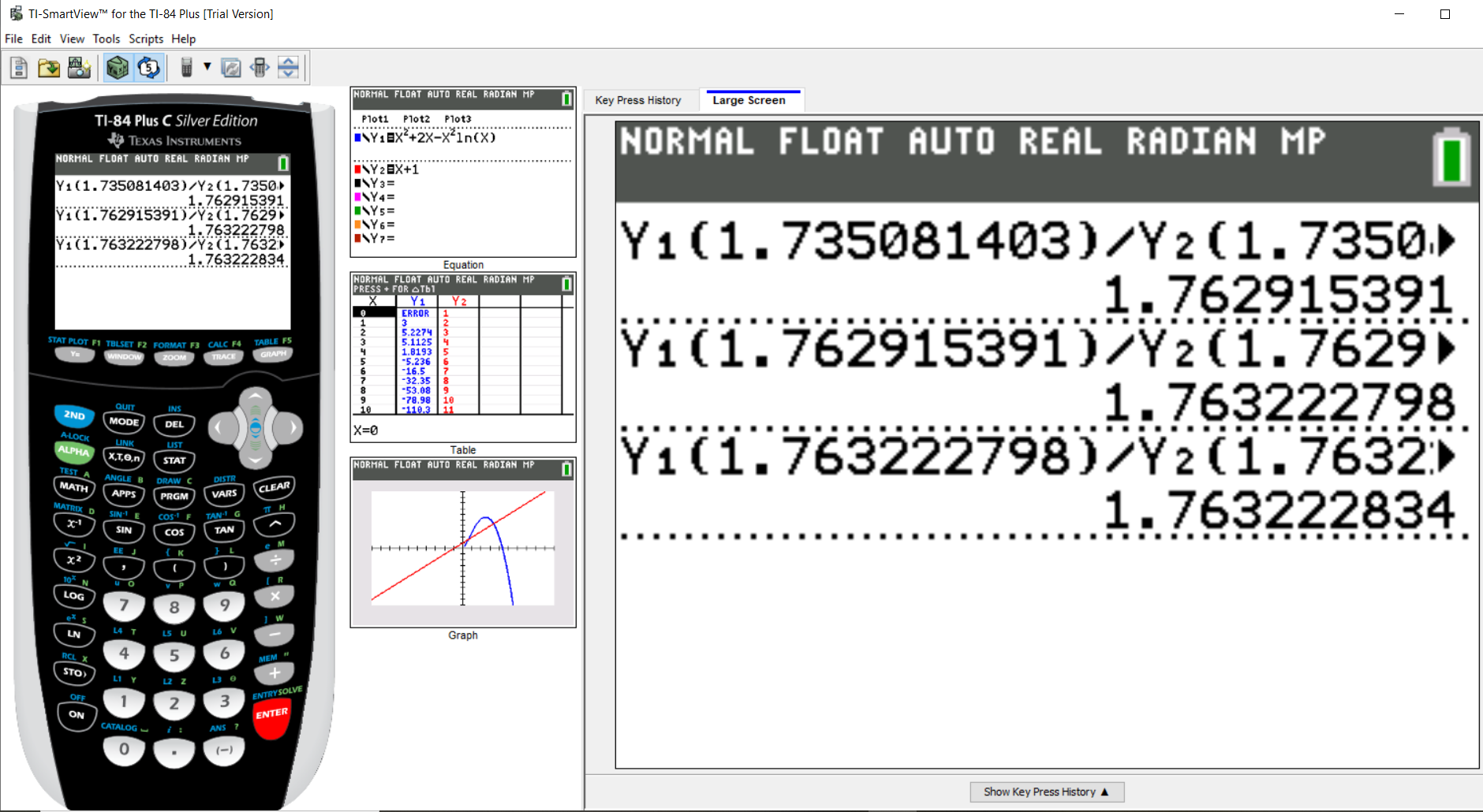
$ x_5 = 1.763222798 \\[3ex] x_6 = 1.763222834 \\[3ex] Because\;\;x_5 \approx x_6...STOP $
(a.) Choosing $x_1 = 1$, determine the exact value of the third approximation, $x_3$ for the root via Newton's method.
(b.) Then, continue to find the root, correct to 5 decimal places, for comparison.
$ (a.) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = 7x^{-1} - 7\ln x \\[3ex] f'(x) = -7x^-2 - \left[7\left(\dfrac{1}{x}\right) + \ln x(0)\right] \\[5ex] f'(x) = -7x^{-2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] Simplify\;\;f(x)\;\;and\;\;f'(x) \\[3ex] f(x) = \dfrac{7}{x} - 7\ln(x) \\[5ex] f(x) = \dfrac{7 - 7x\ln x}{x} \\[5ex] f'(x) = \dfrac{-7}{x^2} - \dfrac{7}{x} \\[5ex] f'(x) = \dfrac{-7 - 7x}{x^2} \\[5ex] \dfrac{f(x)}{f'(x)} \\[5ex] = f(x) \div f'(x) \\[3ex] = \dfrac{7 - 7x\ln x}{x} \div \dfrac{-7 - 7x}{x^2} \\[5ex] = \dfrac{7 - 7x\ln x}{x} * \dfrac{x^2}{-7 - 7x} \\[5ex] = \dfrac{7(1 - x\ln x)}{x} * \dfrac{x^2}{-7(1 + x)} \\[5ex] = \dfrac{x(1 - x\ln x)}{-(1 + x)} \\[5ex] = \dfrac{x - x^2\ln x}{-(1 + x)} \\[5ex] = -\dfrac{(x - x^2\ln x)}{1 + x} \\[5ex] = \dfrac{-x + x^2\ln x}{x + 1} \\[5ex] = \dfrac{x^2\ln x - x}{x + 1} \\[5ex] x - \dfrac{f(x)}{f'(x)} \\[5ex] = x - \dfrac{x^2\ln x - x}{x + 1} \\[5ex] = \dfrac{x(x + 1) - (x^2\ln x - x)}{x + 1} \\[5ex] = \dfrac{x^2 + x - x^2\ln x + x}{x + 1} \\[5ex] = \dfrac{x^2 + 2x - x^2\ln x}{x + 1} \\[5ex] x_{n + 1} = x_n - \dfrac{f(x)}{f'(x)} \\[5ex] \implies \\[3ex] x_{n + 1} = \dfrac{x_n^2 + 2x_n - x_n^2\ln x_n}{x_n + 1} \\[5ex] x_1 = 1 \\[3ex] \implies \\[3ex] x_2 = \dfrac{x_1^2 + 2x_1 - x_1^2\ln x_1}{x_1 + 1} \\[5ex] x_2 = \dfrac{1^2 + 2(1) - 1^2 * \ln(1)}{1 + 1} \\[5ex] x_2 = \dfrac{1 + 2 - 1 * 0}{2} \\[5ex] x_2 = \dfrac{1 + 2 - 0}{2} \\[5ex] x_2 = \dfrac{3}{2} \\[7ex] x_3 = \dfrac{x_2^2 + 2x_2 - x_2^2\ln x_2}{x_2 + 1} \\[5ex] \underline{Numerator} \\[3ex] x_2^2 + 2x_2 - x_2^2\ln x_2 \\[3ex] = \left(\dfrac{3}{2}\right)^2 + 2 * \dfrac{3}{2} - \left(\dfrac{3}{2}\right)^2 * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{9}{4} + 3 - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \\[5ex] \underline{Denominator} \\[3ex] x_2 + 1 \\[3ex] = \dfrac{3}{2} + 1 \\[5ex] = \dfrac{3 + 2}{2} \\[5ex] = \dfrac{5}{2} \\[5ex] Numerator \div Denominator \\[3ex] = \dfrac{21}{4} - \dfrac{9}{4} * \ln \left(\dfrac{3}{2}\right) \div \dfrac{5}{2} \\[5ex] = \dfrac{1}{4}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] * \dfrac{2}{5} \\[5ex] = \dfrac{1}{10}\left[21 - 9\ln\left(\dfrac{3}{2}\right)\right] \\[5ex] = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] \therefore x_3 = \dfrac{21}{10} - \dfrac{9}{10}\ln\left(\dfrac{3}{2}\right) \\[5ex] (b.) \\[3ex] x_3 = 2.1 - (0.9 * \ln(1.5)) \\[3ex] x_3 = 1.735081403 \\[3ex] $


$ x_4 = 1.762915391 \\[3ex] $

$ x_5 = 1.763222798 \\[3ex] x_6 = 1.763222834 \\[3ex] Because\;\;x_5 \approx x_6...STOP $
(30.)