Differential Calculus and Integral Calculus Projects

Objectives

Students will:
(1.) Apply derivatives to solve problems in life sciences, social sciences, and business.
(2.) Use derivatives to model position, velocity, and acceleration.
(3.) Use derivatives to find absolute extrema and to solve optimization problems in life sciences, social sciences, and business.
(4.) Perform implicit differentiation and apply the concept to related rate problems.
(5.) Use integration to solve applications in life sciences such as exponential growth and decay.
(6.) Use integration to solve applications in business and economics, such as future value and consumer and producer's surplus.
(7.) Meet some of the learning objectives of the VCCS (Virginia Community College System) standards for:
MTH 261: Applied Calculus I
(Introduces limits, continuity, differentiation and integration of algebraic, exponential and logarithmic functions, and techniques of integration with an emphasis on applications in business, social sciences and life sciences.)

(8.) Meet the QM (Quality Matters) and USDOE (United States Department of Education) requirements for distance education as regards the provision of RSI (Regular and Substantive Interaction).
Federal Register: Distance Education and Innovation
St. John's University: New Federal Requirements for Distance Education: Regular and Substantive Interaction (RSI)
Student – Content Interaction: Very high
Student – Student Interaction: High
Student – Faculty Interaction: High

Skills Measured/Acquired
(1.) Use of prior and/or existing knowledge.
(2.) Critical Thinking: Write, Paraphrase, Review, Solve, and Interpret.
(3.) Visual Displays and Observations: Graphs.
(4.) Interdisciplinary connections/applications.
(5.) Technology including the use of Artificial Intelligence (AI).
(6.) Research.

Project Requirements

(1.) This is an individual student project.
Students are welcome to interact with one another (Student – Student Interaction), however, each student's work must be different.

For this project, we shall:
(2.) Choose an application from the list and write an applied problem for it.
(a.) Kinematics.
(b.) Exponential Growth (Uninhibited Growth).
(c.) Exponential Growth (Limited Growth).
(d.) Exponential Decay.
(e.) Marginal Analysis (Cost/Revenue/Profit).

Copying the problem directly from online and/or onsite resources verbatim is not acceptable.
Reviewing the problems from online and/or onsite resources and paraphrasing it is required.
Using artificial intelligence to review/proofread the paraphrased problem is highly recommended.

(3.) The applied problem must have these sub-questions at the minimum.
(a.) Write the function from the problem.
The function must have the independent variable and the dependent variable.
(This can be omitted if the applied problem includes the function.)
(b.) Determine the derivative of the function. State the rules used.
(c.) Interpret the derivative in the context of the question.
(d.) Determine the integral of the derivative of the function. State the rules/method used.
(Work through to get back the function.)
(e.) Determine the integral of the function. State the rules/method used.
(f.) Interpret the integral in the context of the question.
(g.) Graph the function.
(h.) Graph the derivative of the function.
(i.) Graph the integral of the function.
(j.) Compare and contrast the graph of the function and the graph of its derivative.
Explain your observations.
(k.) Compare and contrast the graph of the function and the graph of its integral.
Explain your observations.

(4.) Use any of these functions in the applied problem as applicable.
Polynomials.
Power Functions.
Rational Functions.
Radical Functions.
Absolute Value Functions.
Exponential Functions (includes Natural Exponential Functions).
Logarithmic Functions (includes Natural Logarithmic Functions).
Logistic Functions.

(5.) All work/steps must be shown.
Points will be deducted for any missing step.
Do not round intermediate values.
If you must round the final answer, write the entire calculated values first (using the approved calculators listed in your course syllabus). Then, specify the rounding rule used to round the final answer.

(6.) As a VCCS student, you have free access to Microsoft Office suite of apps.
(a.) Please download the desktop apps of Microsoft Office on your desktop/laptop (Windows and/or Mac only).
As specified in your course syllabus, please
Do not use a chromebook.
Do not use a tablet/iPad.
Do not use a smartphone.

( Please contact the IT/Tech Support of your school for assistance if you do not know how to download the desktop app of Microsoft Office.
Alternatively, you may come and see me during Student Engagement Hours and I shall walk with you to BRCC's IT office. )

In that regard, the project is to be typed using the desktop version/app of Microsoft Office Word only. Do not use the web app/sharepoint access of Microsoft Office. Use only the desktop app.

(b.) The file name for the Microsoft Office Word project should be saved as: firstName–lastName–project
Use only hyphens between your first name and your last name; and between your last name and the word, project.
No spaces.

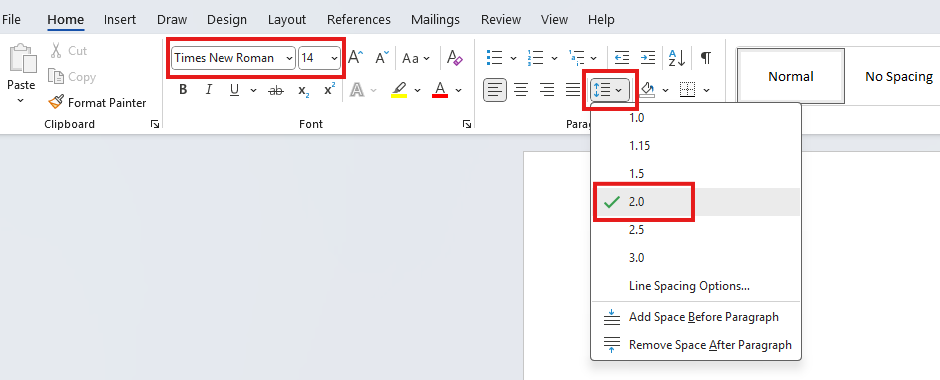
(c.) For all English terms/work: use Times New Roman; font size of 14; line spacing of 2.0 (double-line spacing).
Further, please make sure you have appropriate spacing between each heading and/or section as applicable.
Your work should be well-formatted and visually appealing.



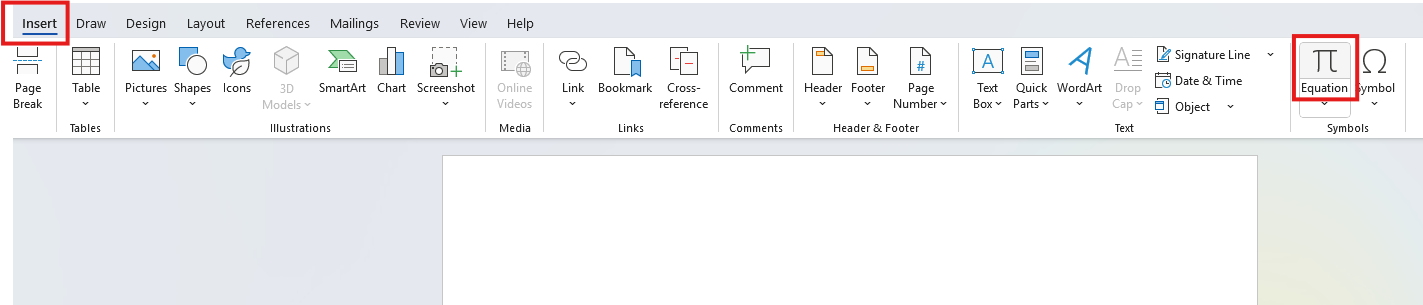
(d.) (i.) For all Math terms/work: symbols, variables, numbers, formulas, expressions, equations and fractions among others, the Math Equation Editor is required.
Please maintain the font size of 14.
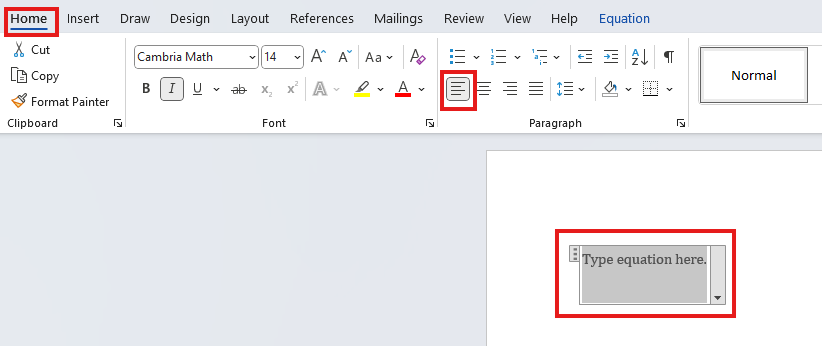
Click the Insert tab, then the Equation (Π) button.



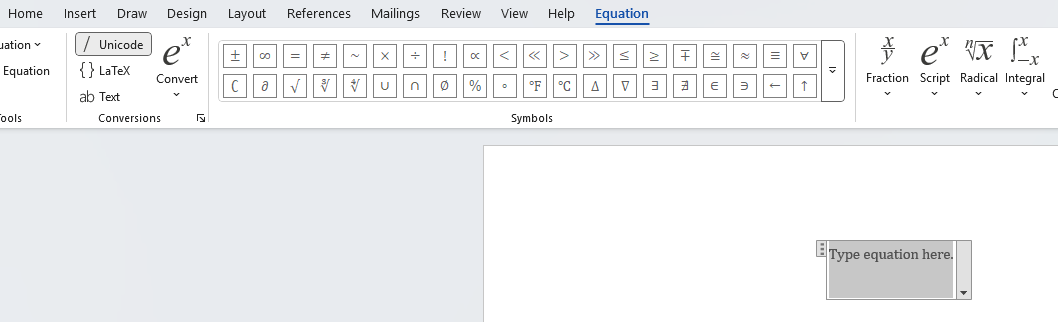
(ii.) By default, the font is set to Cambria Math (set it to that font if it is not) and aligned in the middle.



Please align it to the left.





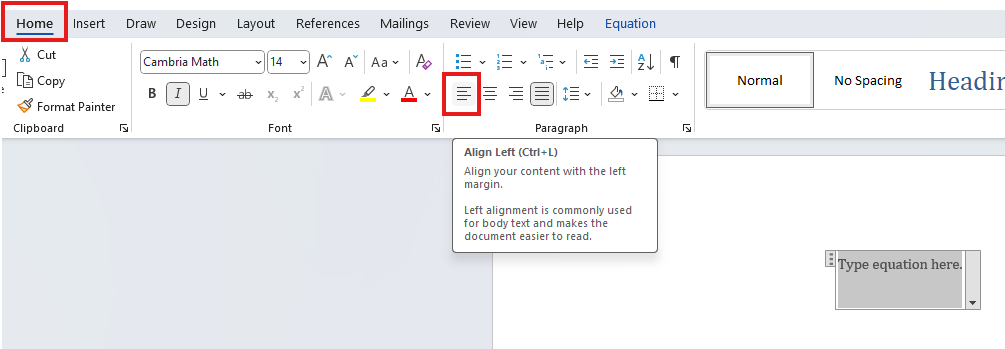
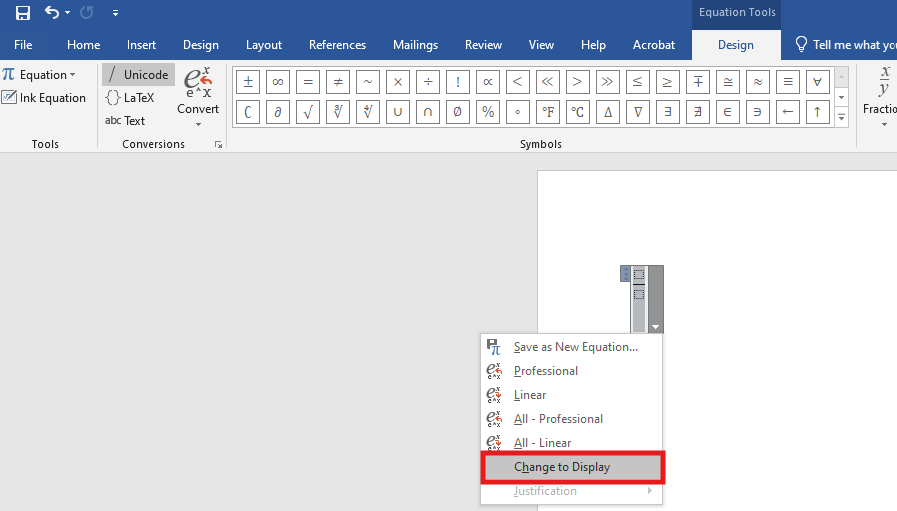
(iii.) Also, please ensure that all Math work in the Math Equation Editor is always set to Change to Display.
It is set to Display by default, however, sometimes the editor misbehaves and setis it to inline rather than to Display. In that case, please set it to Display.



(iv.) Your work should be well-formatted, organized, well-spaced (not compact), and visually appealing.

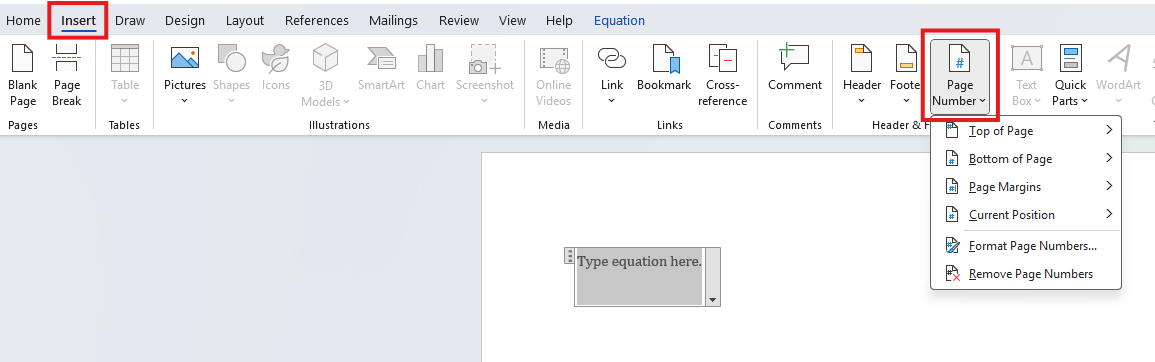
(e.) Include page numbers.
You may include page numbers at the top of the pages or at the bottom of the pages but not both.



(f.) Lists must be ordered and enclosed in parenthesis.
Bulleted lists/bullets are not allowed.
Hyphens should not be used as lists.

(g.) This is a formal academic paper.
Please proof-read all work.
Points will be deducted for mechanical accuracy errors.
For each instance of "i" when written alone, "im", "ive", and similar instances, one point is deducted.

(h.) All graphs must be generated using technology, not drawn freehand.
They should be large, clearly visible, neatly formatted, and appropriately labeled.
Both axis must include scales, and each graph should have a descriptive title.

(7.) Please review the example guides.
You may do similar examples but you may not do the exact examples that I did.
Those example guides are the minimum expectations.
Please go above and beyond if you wish.

(8.) Mr. C (SamDom For Peace) wants you to do this real-world project very well.
Hence, he highly recommends that you submit a draft so he can give you feedback.
Draft projects are not graded because they are drafts. They are only for feedback.
Submitting drafts is highly recommended.
If your professor gives you an opportunity to submit a draft, please use that opportunity.
Submitting drafts is not required.
It is highly recommended because I want to give you the opportunity to do your project very well and make an excellent grade in it.

There are two ways you may submit your draft.
If you would like your colleagues to read my feedback and learn from it, please turn in your draft in the Discussions page → Projects: Drafts forum in the Canvas course. If you do not want your colleagues to read my feedback, please send it to my school email address (the email address provided to you in the course syllabus).
I shall review and provide feedback.
Then, please review my feedback and make changes as necessary.
Keep working with me until I give you the green light to turn in your actual project.
This must be done before the final due date to turn in the actual project.

When everything is fine (after you make changes as applicable based on my feedback), please submit your work in the appropriate place: Assignments page → Projects in the Canvas course.
Only the projects submitted in the appropriate place in the Canvas course are graded.
Please note that any project submitted via email is not graded.

(9.) All work must be turned in by the final due date to receive credit.
Please note the due dates listed in the course syllabus for the submission of the draft and the actual project. In the course syllabus, we have the:
(a.) Initial due date for the Project Draft: Please turn in your draft.

(b.) Initial due date for the Project: If your draft is not ready for submission, keep working with me. Make changes based on my feedback and keep working with me.
If you prefer not to turn in a draft, please review all the resources provided for you and do your project well and submit.

(c.) Final due date for the Project Draft: This is necessary if you want a written feedback for your draft.
After this date, written feedback would not be provided for your draft. However, verbal feedback will be provided during Student Engagement Hours/Live Sessions.

(d.) Final due date for the Project: All work must be turned in the Canvas course: Assignments: Projects section by this date to receive credit.
After this date, no work may be accepted.

(10.) Required Information for the Applied Calculus Project.
Student Name:     .......   .......
Date:     .......
Instructor:     Samuel Chukwuemeka
Application:     Write the specific application
Objectives:     Write the specific objectives.
Questions: and Answers:
Write each specific sub-question.
Answer each sub-question.
References:
Cite your source(s) accordingly.
Indicate the type of citation format.

Example Guides

Please review these example guides.
I attempted some of the questions.
If you need help with any of the questions, please contact me via my school email and/or attend the Student Engagement Hours/Live Sessions onsite or online.

1st Application: Kinematics

For the objectives, you may use the expanded form or the condensed form.
You do not need to indicate the form.
Objectives. (Expanded Form)
(1.) Problem Formulation: I will write an applied problem in kinematics that models vertical motion.
(2.) Function Construction: I will formulate the mathematical function that represents the motion described in the problem.
(3.) Function Analysis: I will graph the function and interpret its physical meaning in the context of motion.
(4.) Derivative Determination: I will compute the derivative of the function and explain its significance for example, the interpretation of the velocity as the rate of change of position.
(5.) Derivative Graphing: I will graph the derivative and interpret its behavior in relation to the original function.
(6.) Integral of the Derivative: I will determine the integral of the derivative to recover the original function and interpret the result.
(7.) Integral of the Function: I will compute the integral of the function and interpret its meaning for example, interpreting it as the accumulated displacement–time area.
(8.) Integral Graphing: I will graph the integral and interpret its behavior in the context of motion.
(9.) Comparative Analysis: Function versus Derivative I will compare and contrast the graph of the function with the graph of its derivative, identifying relationships between position and velocity.
(10.) Comparative Analysis: Function versus Integral I will compare and contrast the graph of the function with the graph of its integral, identifying relationships between position and accumulated displacement.

Objectives. (Condensed Form)
(1.) Modeling Motion: I will formulate mathematical functions from applied kinematics problems and represent them graphically.
(2.) Differentiation and Interpretation: I will compute and interpret the derivative of motion function, graph it, and explain its physical significance, for example the interpretation of velocity as the rate of change of position.
(3.) Integration and Interpretation: I will compute and interpret integrals of motion function and its derivative, graph them, and explain their physical meanings.
(4.) Comparative Analysis: I will compare and contrast the graphs of a function, its derivative, and its integral to highlight the relationships among position, velocity, and accumulated displacement.

Questions.
A ball is projected vertically upward from an initial height, h₀ of 2 feet with an initial velocity, v₀ of 28 feet per second.
Take the acceleration due to gravity, g ≈ 32 feet per second squared.

(1.) Determine the height function, h(t) that gives the height of the ball in feet, t seconds after it has been thrown.
(2.) Sketch and interpret the graph of the function.
(3.) Determine the derivative of the function. State the differentiation rules used.
(4.) Interpret the derivative.
(5.) Sketch and interpret the graph of the derivative.
(6.) Determine the integral of the derivative of the function. State the integration rules/method used.
(7.) Interpret the integral of the derivative.
(8.) Determine the integral of the height function. State the integration rules/method used.
(9.) What does Number (8.) represent mathematically? Does it have a physical interpretation?.
(10.) Sketch and interpret the graph of the integral.
(11.) Compare and contrast the graph of the function and the graph of its derivative.
Explain your observations.
(12.) Compare and contrast the graph of the function and the graph of its integral.
Explain your observations.

Solutions.
Because the ball is projected upward and the acceleration due to gravity, g acts downwards, we shall use the negative value of g as the acceleration, a
Under a constant acceleration, the position function is given by:

$ (1.)\text{ Function} \\[3ex] h(t) = \dfrac{1}{2}at*2 + v_0t + h_0 \\[5ex] \text{where } a = -g = -32\;ft/sec^2 \\[3ex] v_0 = 28\;ft/sec \\[3ex] h_0 = 2\;ft \\[3ex] \implies \\[3ex] h(t) = \dfrac{1}{2}a * -32 * t^2 + 28 * t + 2 \\[5ex] h(t) = -16t^2 + 28t + 2 \\[7ex] (3.)\text{ Derivative} \\[3ex] \dfrac{dh}{dt} = -32t + 28...\text{Power Rule of Differentiation} \\[7ex] (6.)\text{ Integral of the Derivative} \\[3ex] dh = (-32t + 28)\; dt \\[3ex] \displaystyle\int dh = \displaystyle\int (-32t + 28)\; dt \\[3ex] h = -\dfrac{32t^2}{2} + 28t + C ...\text{Power Rule of Integration} \\[5ex] h(t) = -16t^2 + 28t + C ...\text{where C is the constant of integration} \\[3ex] \text{When } t = 0 \\[3ex] h(0) = -16(0)^2 + 28(0) + C \\[3ex] h(0) = C = 2 \\[3ex] \implies \\[3ex] h(t) = -16t^2 + 28t + 2 \\[7ex] (8.)\text{ Integral of the Function} \\[3ex] \displaystyle\int h(t)\; dt = \displaystyle\int (-16t^2 + 28t + 2)\; dt \\[3ex] = -\dfrac{16t^3}{3} + \dfrac{28t^2}{2} + 2t + C ...\text{Power Rule of Integration} \\[5ex] = -\dfrac{16t^3}{3} + 14t^2 + 2t + C ...\text{where C is the constant of integration} $

2nd Application: Exponential Growth: (Uninhibited Growth): Epidemics

For the objectives, you may use the expanded form or the condensed form.
You do not need to indicate the form.
Objectives. (Expanded Form)
(1.) Problem Formulation: I will analyze an applied problem in epidemiology that models the exponential growth of AIDS cases in the United States during the early 1980s.
(2.) Function Construction: I will formulate the exponential function N(t) that predicts the number of AIDS cases, where t represents years after the start of 1983.
(3.) Function Analysis: I will sketch the graph of N(t) and interpret its shape in the context of disease spread, explaining how exponential growth reflects the rapid increase in cases.
(4.) Derivative Determination: I will compute the derivative of the function and state the differentiation rules used, and explain its significance as the rate of change in the number of cases.
(5.) Derivative Graphing: I will sketch the graph of the derivative and and interpret its behavior in relation to the original function, highlighting how the rate of new cases grows alongside total cases.
(6.) Integral of the Derivative: I will determine the integral of the derivative to recover the original function and interpret this result as an illustration of the Fundamental Theorem of Calculus.
(7.) Integral of the Function: I will compute the integral of the function, state the integration rules used, and interpret its meaning in context, for example as the accumulated “case-years” over time.
(8.) Integral Graphing: I will sketch the graph of the integral and interpret its behavior in the context of cumulative disease burden.
(9.) Comparative Analysis: Function versus Derivative I will compare and contrast the graph of the function with the graph of its derivative, identifying relationships between the total number of cases and the rate of new cases.
(10.) Comparative Analysis: Function versus Integral I will compare and contrast the graph of the function with the graph of its integral, identifying relationships between the number of cases at a given time and the accumulated case-time measure.

Objectives. (Condensed Form)
(1.) Modeling Epidemic Growth: I will formulate an exponential function N(t) to model the growth of AIDS cases in the U.S. t years after the start of 1983, and represent it graphically in context.
(2.) Differentiation and Interpretation: I will compute and interpret the derivative, sketch its graph, and explain its significance as the rate of new cases over time.
(3.) Integration and Interpretation: I will compute and interpret integrals of exponential function and its derivative, sketch their graphs, and explain their meanings in context, such as cumulative case-years and the Fundamental Theorem of Calculus.
(4.) Comparative Analysis: I will compare and contrast the graphs of the function, its derivative, and its integral to highlight the relationships among total cases, rate of new cases, and accumulated burden of a disease.

Questions.
Between 1982 and 1985, the Acquired Immune Deficiency Syndrome (AIDS) cases in the U.S. followed an exponential (uninhibited) growth pattern, before beginning to diverge from the pure exponential trend in subsequent years.
From the data based on regression of the 1982 – 1986 figures, the number of cases in the United States was increasing by about 50% every 6 months.
By the start of 1983, there were approximately 1,600 AIDS cases in the United States.
[Source for data: Centers for Disease Control and Prevention. HIV/AIDS Surveillance Report, 2000;12 (No. 2).]

(1.) Determine the exponential function, N(t) that predicts the number of of AIDS cases in the U.S., t years after the start of 1983.
(2.) Sketch the graph of N(t). Interpret its shape in the context of disease spread.
(3.) Determine the derivative of the function. State the differentiation rules used.
(4.) Interpret the derivative.
(5.) Sketch and interpret the graph of the derivative.
(6.) Determine the integral of the derivative of the function. State the integration rules/method used.
(7.) Interpret the integral of the derivative.
(8.) Determine the integral of the function. State the integration rules/method used.
(9.) Interpret the integral of the function.
(10.) Sketch and interpret the graph of the integral.
(11.) Compare and contrast the graph of the function and the graph of its derivative.
Explain your observations.
(12.) Compare and contrast the graph of the function and the graph of its integral.
Explain your observations.

Solutions.
N₀ = number of of AIDS cases in the U.S. at the start of 1983 ≈ 1600 people.
N(t) = number of of AIDS cases in the U.S. t years after the start of 1983.
b = base

$ (1.)\text{ Function} \\[3ex] N(t) = N_0 * b^t...\text{General form of an Exponential Function} \\[3ex] N_0 = 1600\text{ people}...\text{ start of 1983 corresponding to } 1983 = 0 \\[3ex] N(0) = 1600 * b^0 \\[3ex] N(0) = 1600 * 1 \\[3ex] N(0) = N_0 = 1600\text{ people} \\[5ex] 6\;months = \dfrac{6}{12}\text{ year} = \dfrac{1}{2}\text{ year} \\[5ex] 50\%\text{ of 1600} = \dfrac{50}{100} * 1600 = 800\text{ people} \\[5ex] 50\%\text{ increase} = 1600 + 800 = 2400\text{ people} \\[3ex] \text{At } t = 0.5 \\[3ex] N(0.5) = 1600 * b^{0.5} \\[3ex] 2400 = 1600 * b^{0.5} \\[3ex] b^{0.5} = \dfrac{2400}{1600} = \dfrac{3}{2} \\[5ex] \text{Square both sides} \\[3ex] (b^{0.5})^2 = \left(\dfrac{3}{2}\right)^2 \\[5ex] b = \dfrac{9}{4} \\[5ex] \implies \\[3ex] N(t) = 1600 * \left(\dfrac{9}{4}\right)^t \\[9ex] (3.)\text{ Derivative} \\[3ex] \dfrac{dN}{dt} = 1600 * \left(\dfrac{9}{4}\right)^t \ln \dfrac{9}{4} + \left(\dfrac{9}{4}\right)^t * 0 \\[5ex] ...\text{Product Rule of Differentiation and Exponential Derivative Rule} \\[5ex] \dfrac{dN}{dt} = 1600 \left(\dfrac{9}{4}\right)^t \ln \dfrac{9}{4} \\[9ex] (6.)\text{ Integral of the Derivative} \\[3ex] dN = \left[1600 \left(\dfrac{9}{4}\right)^t \ln \dfrac{9}{4}\right]\; dt \\[5ex] \displaystyle\int dN = \displaystyle\int \left[1600 \left(\dfrac{9}{4}\right)^t \ln \dfrac{9}{4}\right]\; dt \\[5ex] N(t) = 1600\ln\dfrac{9}{4} \displaystyle\int \left(\dfrac{9}{4}\right)^t\; dt \\[5ex] N(t) = 1600\ln\dfrac{9}{4} * \dfrac{\left(\dfrac{9}{4}\right)^t}{\ln\dfrac{9}{4}} + C ...\text{where C is the constant of integration} \\[10ex] N(t) = 1600\left(\dfrac{9}{4}\right)^t + C \\[5ex] \text{When } t = 0 \\[3ex] N(0) = 1600\left(\dfrac{9}{4}\right)^0 + C \\[5ex] 1600 = 1600 * 1 + C \\[3ex] 1600 = 1600 + C \\[3ex] C = 1600 - 1600 \\[3ex] C = 0 \\[3ex] \implies \\[3ex] N(t) = 1600\left(\dfrac{9}{4}\right)^t + 0 \\[5ex] N(t) = 1600\left(\dfrac{9}{4}\right)^t \\[9ex] (8.)\text{ Integral of the Function} \\[3ex] \displaystyle\int N(t)\; dt = \displaystyle\int 1600\left(\dfrac{9}{4}\right)^t\; dt \\[5ex] = 1600 \displaystyle\int \left(\dfrac{9}{4}\right)^t\; dt \\[5ex] = 1600 * \dfrac{\left(\dfrac{9}{4}\right)^t}{\ln\dfrac{9}{4}} + C ...\text{Exponential Rule of integration} \\[10ex] = \dfrac{1600\left(\dfrac{9}{4}\right)^t}{\ln\dfrac{9}{4}} + C ...\text{where C is the constant of integration} $

Grading Rubric

Students Projects

References