Welcome to Week 2: Average Rate of Change
Great Students,
Greetings to everyone.
Welcome to Module 2.
In Module 1, we discussed the topics of Limits and Continuity.
In this module, let us see an important application of limit: the Average Rate of Change, otherwise
known as the Slope.
Recall:
PreAlgebra:
(1.) We defined slope as the ratio of the change in the output value of the function with respect
to
(wrt) a unit change in the input value of the function.
It is also known as the average rate of change.
Considering a two-dimensional coordinate system where $y = f(x)$
y = dependent variable
x = independent variable
For a Linear Graph (Graph of a Linear Function) which is a straight line graph,
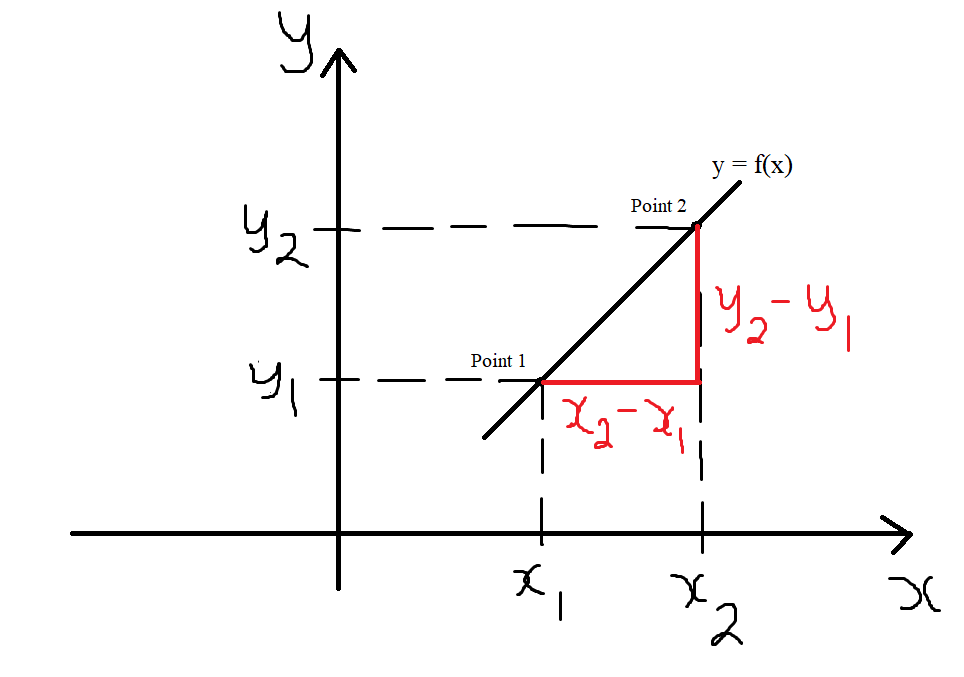
$
\text{Point 1 } (x_1, y_1) \\[3ex]
x_1 = \text{initial value of } x \\[3ex]
y_1 = \text{initial value of } y \\[5ex]
\text{Point 2 } (x_1, y_1) \\[3ex]
x_2 = \text{final value of } x \\[3ex]
y_2 = \text{final value of } y \\[3ex]
\text{Change} = \text{final value} - \text{initial value} \\[3ex]
\text{Change in } x = \Delta x = x_2 - x_1 \\[3ex]
\text{Change in } y = \Delta y = y_2 - y_1 \\[3ex]
\text{Slope, } m \\[3ex]
= \dfrac{\Delta y}{\Delta x} \\[5ex]
= \dfrac{y_2 - y_1}{x_2 - x_1} \\[5ex]
$
In this example, both changes are positive.
Hence, the slope is also positive.
As the value of x increases, the value of y also increases.
This implies that the rate of change of y per unit change of x is positive.
Algebra:
(2.) We defined these terms:
(a.) The secant line to a curve is the line segment that intersects two points on
the curve.
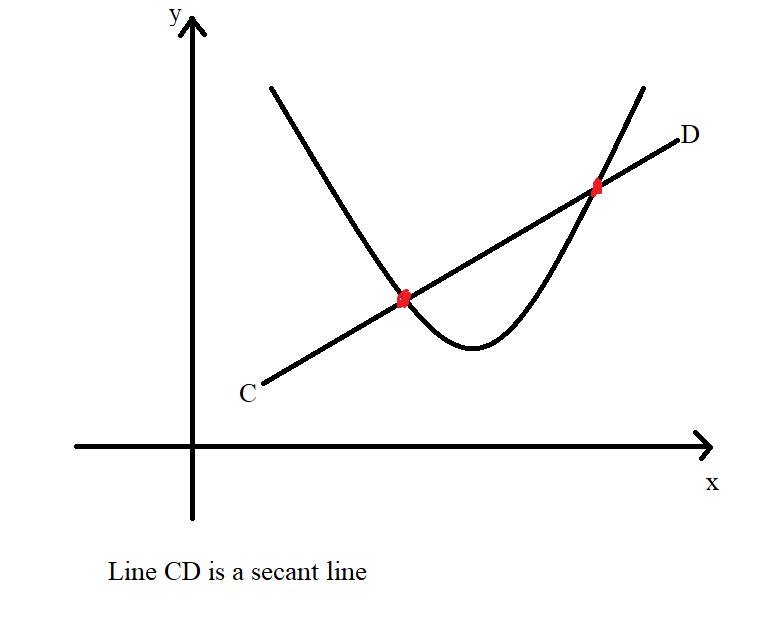
(b.) The tangent line to a curve is the line that touches only one point on the
curve.
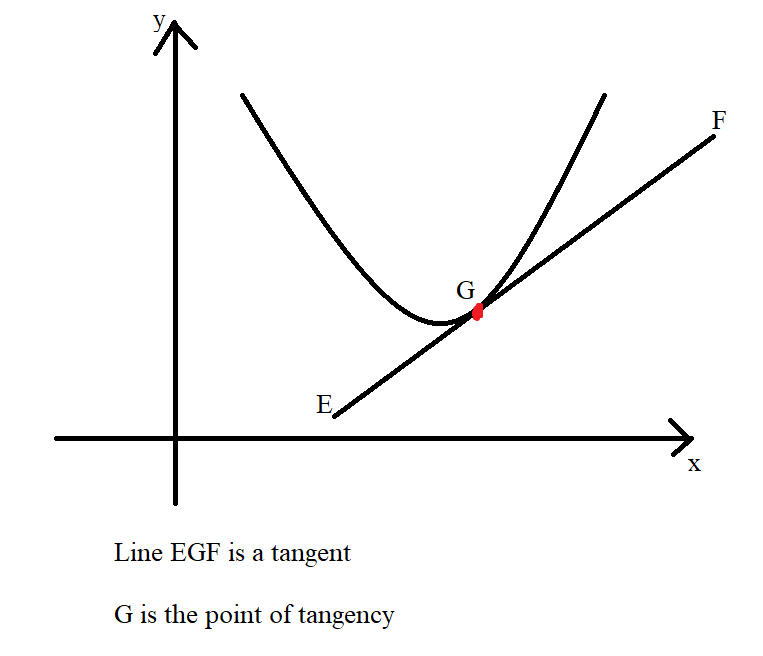
(Notice the terms: intersects, two points, touches, one point)
(3.) We reviewed the Difference Quotient of a function and noted these definitions.
We noted that:
(a.) The difference quotient of a function is the slope of the secant line.
(b.) The derivative of a function is the slope of the tangent line.
(4.) We also noted that for:
the graph of all linear functions (straight-line graph):
the slope of the line is the same at every point on the graph/line.
Depending on the graph, the slope can be positive, negative, zero, or undefined.
Calculus:
But, how do we find the slope of non-linear graphs (curves)?
For example, how do we find the slope of a: parabola? graph of a cubic function? graph of a quartic
function? etc.
Well, here comes Calculus!
The derivative of the function, which is the slope of the tangent line is the limit of the
difference quotient of the function.
Welcome to Average Rate of Change.
May you please:
(1.) Click the Week 2 module.
(2.) Review the Learning Objectives.
(3.) Review the Readings/Assessments.
(4.) Complete the assessments initially due this week.
(5.) Participate in the Week 2 Discussion (DB 2).
(6.) Attend the Live Sessions/Student Engagement Hours for this week.
Should you have any questions, please ask. I am here to help.
Thank you.
Samuel Chukwuemeka
Working together for success